
- 機器學習基礎
- ML - 首頁
- ML - 簡介
- ML - 入門
- ML - 基本概念
- ML - 生態系統
- ML - Python 庫
- ML - 應用
- ML - 生命週期
- ML - 所需技能
- ML - 實現
- ML - 挑戰與常見問題
- ML - 限制
- ML - 現實生活中的例子
- ML - 資料結構
- ML - 數學
- ML - 人工智慧
- ML - 神經網路
- ML - 深度學習
- ML - 獲取資料集
- ML - 分類資料
- ML - 資料載入
- ML - 資料理解
- ML - 資料準備
- ML - 模型
- ML - 監督學習
- ML - 無監督學習
- ML - 半監督學習
- ML - 強化學習
- ML - 監督學習與無監督學習
- 機器學習資料視覺化
- ML - 資料視覺化
- ML - 直方圖
- ML - 密度圖
- ML - 箱線圖
- ML - 相關矩陣圖
- ML - 散點矩陣圖
- 機器學習統計學
- ML - 統計學
- ML - 均值、中位數、眾數
- ML - 標準差
- ML - 百分位數
- ML - 資料分佈
- ML - 偏度和峰度
- ML - 偏差和方差
- ML - 假設
- ML中的迴歸分析
- ML - 迴歸分析
- ML - 線性迴歸
- ML - 簡單線性迴歸
- ML - 多元線性迴歸
- ML - 多項式迴歸
- ML中的分類演算法
- ML - 分類演算法
- ML - 邏輯迴歸
- ML - K近鄰演算法(KNN)
- ML - 樸素貝葉斯演算法
- ML - 決策樹演算法
- ML - 支援向量機
- ML - 隨機森林
- ML - 混淆矩陣
- ML - 隨機梯度下降
- ML中的聚類演算法
- ML - 聚類演算法
- ML - 基於中心點的聚類
- ML - K均值聚類
- ML - K中心點聚類
- ML - 均值漂移聚類
- ML - 層次聚類
- ML - 基於密度的聚類
- ML - DBSCAN聚類
- ML - OPTICS聚類
- ML - HDBSCAN聚類
- ML - BIRCH聚類
- ML - 親和傳播
- ML - 基於分佈的聚類
- ML - 凝聚層次聚類
- ML中的降維
- ML - 降維
- ML - 特徵選擇
- ML - 特徵提取
- ML - 後退消除法
- ML - 前向特徵構建
- ML - 高相關性過濾器
- ML - 低方差過濾器
- ML - 缺失值比率
- ML - 主成分分析
- 強化學習
- ML - 強化學習演算法
- ML - 利用與探索
- ML - Q學習
- ML - REINFORCE演算法
- ML - SARSA強化學習
- ML - 演員-評論家方法
- 深度強化學習
- ML - 深度強化學習
- 量子機器學習
- ML - 量子機器學習
- ML - 使用Python的量子機器學習
- 機器學習雜項
- ML - 效能指標
- ML - 自動工作流
- ML - 提升模型效能
- ML - 梯度提升
- ML - 自舉匯聚(Bagging)
- ML - 交叉驗證
- ML - AUC-ROC曲線
- ML - 網格搜尋
- ML - 資料縮放
- ML - 訓練和測試
- ML - 關聯規則
- ML - Apriori演算法
- ML - 高斯判別分析
- ML - 成本函式
- ML - 貝葉斯定理
- ML - 精確率和召回率
- ML - 對抗性
- ML - 堆疊
- ML - 時期
- ML - 感知器
- ML - 正則化
- ML - 過擬合
- ML - P值
- ML - 熵
- ML - MLOps
- ML - 資料洩露
- ML - 機器學習的貨幣化
- ML - 資料型別
- 機器學習 - 資源
- ML - 快速指南
- ML - 速查表
- ML - 面試問題
- ML - 有用資源
- ML - 討論
機器學習中的簡單線性迴歸
什麼是簡單線性迴歸?
簡單線性迴歸是一種統計學和監督學習方法,其中使用單個自變數(也稱為預測變數)來預測因變數。換句話說,它模擬因變數與單個自變數之間的線性關係。
機器學習中的簡單線性迴歸是線性迴歸的一種型別。當線性迴歸演算法處理單個自變數時,稱為簡單線性迴歸。當存在多個自變數(特徵變數)時,稱為多元線性迴歸。
自變數
資料集中特徵輸入稱為自變數。簡單線性迴歸中只有一個自變數。自變數也稱為預測變數,因為它用於預測目標值。它繪製在水平軸上。
因變數
資料集中目標值稱為因變數。它也稱為響應變數或預測變數。它繪製在垂直軸上。
迴歸線
在簡單線性迴歸中,迴歸線是一條最適合資料點的直線,用於顯示因變數和自變數之間的關係。
圖形表示
下圖描述了簡單線性迴歸模型 -
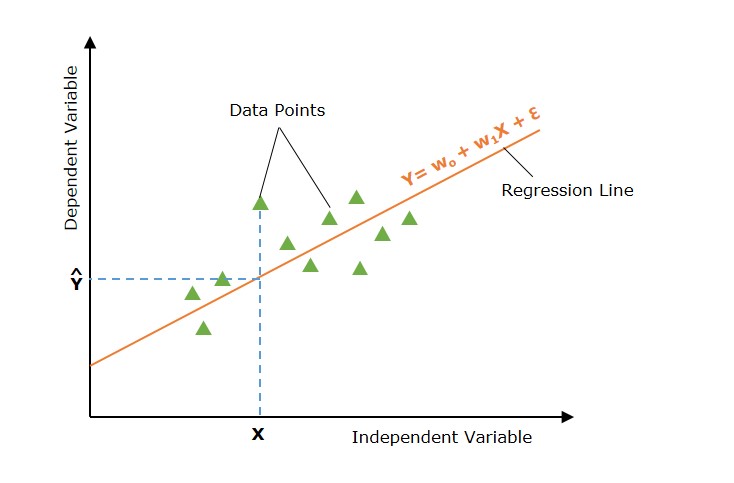
在上圖中,直線表示簡單線性迴歸線,其中Ŷ是預測值,Y是因變數(目標),X是自變數(輸入)。
簡單線性迴歸模型
機器學習中的簡單線性迴歸模型可以用以下數學方程式表示 -
$$\mathrm{ Y = w_0 + w_1 X + \epsilon }$$
其中
- Y 是因變數(目標)。
- X 是自變數(特徵)。
- w0 是線的 y 截距。
- w1 是線的斜率,表示 X 對 Y 的影響。
- ε 是誤差項,捕獲 X 未解釋的 Y 中的變化。
簡單線性迴歸如何工作?
簡單線性迴歸的主要目的是找到穿過資料點並使實際值與預測值之間的差異最小化的最佳擬合線(直線)。
定義假設函式
在簡單線性迴歸中,假設是因變數(輸出/目標)和自變數(輸入)之間存線上性關係。這種線性關係可以使用線性方程表示 -
$$\mathrm{\hat{Y} = w_0 + w_1 X}$$
使用引數 w0 和 w1 的不同值,存在多個線性方程(直線)。所有此類線性方程(所有直線)的集合稱為假設空間。
現在,簡單線性迴歸模型的主要目標是在假設空間(所有直線的集合)中找到最佳擬合線。
找到最佳擬合線
現在任務是找到最佳擬合線(迴歸線)。為此,我們定義一個成本函式或損失函式來衡量實際值與預測值之間的差異。
為了找到最佳擬合線,簡單線性迴歸模型會初始化(使用預設值)迴歸線的引數。此迴歸線(使用初始化的引數)用於找到給定輸入值的預測值。
簡單線性迴歸的損失函式
現在使用輸入值和預測值,我們計算損失函式。損失函式用於找到引數的最佳值。
損失函式找到輸入值與預測值之間的差異。簡單線性迴歸中使用了不同的損失函式,例如均方誤差 (MSE)、平均絕對誤差 (MEA)、R 平方等。最常用的損失函式是均方誤差。
簡單線性迴歸的損失函式(以均方誤差表示)如下 -
$$\mathrm{J(w_0, w_1) = \frac{1}{2n} \sum_{i=1}^{n} \left( Y_i - \hat{Y}_i \right)^2}$$
最佳化
引數的最佳值是使成本函式最小化的那些值。找到最佳值是一個迭代過程,其中引數被迭代更新。
簡單線性迴歸中應用了許多最佳化技術。梯度下降是一種簡單且最常用的最佳化技術,用於簡單線性迴歸。
具有最佳引數值的線性方程是最佳擬合線(迴歸線),它是簡單線性迴歸問題的最終解決方案。此線用於預測新的和看不見的資料。
簡單線性迴歸的假設
簡單線性迴歸模型對資料集做出了一些假設。以下是一些假設 -
- 線性 - 此假設假設因變數和自變數之間的關係是線性的。這意味著隨著自變數的變化,因變數線性變化。散點圖將顯示資料集中線性關係。
- 同方差性 - 對於所有觀察值,殘差的方差相同。此假設與殘差平方有關。
- 獨立性 - 示例(觀察值或 X 和 Y 對)是獨立的。資料中不存在共線性,因此殘差不會相關。要檢查這一點,我們檢視殘差與擬合的散點圖。
- 正態性 - 模型殘差服從正態分佈。殘差是實際值和預測值之間的差異。為了檢查正態性,我們檢查殘差的直方圖。直方圖應該近似服從正態分佈。
使用 Python 實現簡單線性迴歸演算法
為了實現簡單線性迴歸演算法,我們使用一個包含兩個變數的資料集:工作年限(自變數)和薪資(因變數)。
這裡,我們使用以下資料集。資料集包含 30 個數據點的示例。您可以建立一個 CSV 檔案並將這些資料點儲存在其中。
Salary_Data.csv
| 工作年限 | 薪資 |
|---|---|
| 1.1 | 39343 |
| 1.3 | 46205 |
| 1.5 | 37731 |
| 2 | 43525 |
| 2.2 | 39891 |
| 2.9 | 56642 |
| 3 | 60150 |
| 3.2 | 54445 |
| 3.2 | 64445 |
| 3.7 | 57189 |
| 3.9 | 63218 |
| 4 | 55794 |
| 4 | 56957 |
| 4.1 | 57081 |
| 4.5 | 61111 |
| 4.9 | 67938 |
| 5.1 | 66029 |
| 5.3 | 83088 |
| 5.9 | 81363 |
| 6 | 93940 |
| 6.8 | 91738 |
| 7.1 | 98273 |
| 7.9 | 101302 |
| 8.2 | 113812 |
| 8.7 | 109431 |
| 9 | 105582 |
| 9.5 | 116969 |
| 9.6 | 112635 |
| 10.3 | 122391 |
| 10.5 | 121872 |
此實現的目的是什麼?
構建這個簡單線性迴歸模型的目的是確定哪條線最能代表這兩個變數之間的關係。
以下是使用 Python 實現簡單線性迴歸模型的步驟:
步驟 1:資料準備
資料準備或預處理是第一步。我們有一個名為“Salary_Data.csv”的 CSV 檔案作為資料集,如上所述。
在匯入資料集和構建簡單線性迴歸模型之前,我們需要匯入 Python 庫。
import numpy as np import matplotlib.pyplot as plt import pandas as pd
載入資料集
dataset = pd.read_csv('Salary_Data.csv')
然後必須從提供的資料集中提取因變數 (X) 和自變數 (Y)。工作年限(YearsExperience)是自變數,Salary 是因變數。
X = dataset.iloc[:, :-1].values y = dataset.iloc[:, -1].values
讓我們檢查資料集的前五個示例。
print(dataset.head())
輸出
0 1.1 39343.0 1 1.3 46205.0 2 1.5 37731.0 3 2.0 43525.0 4 2.2 39891.0
讓我們檢查資料集是否線性
plt.scatter(X, y, color="green")
plt.title("Salary vs Experience")
plt.xlabel("Years of Experience")
plt.ylabel("Salary (INR)")
plt.show()
輸出
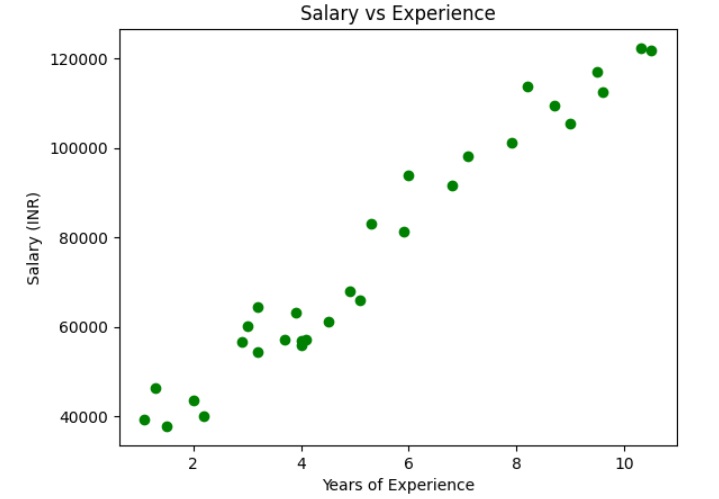
上圖顯示自變數和因變數之間存線上性關係。因此,我們可以對資料集應用簡單線性迴歸,以找到這些變數之間最佳的關係。
將資料集分成訓練集和測試集
然後將訓練集和測試集分成兩組。我們將使用 80% 的觀測值作為訓練集,20% 的觀測值作為測試集,從我們擁有的總共 30 個觀測值中。因此,訓練集中將有 24 個觀測值,測試集中將有 6 個觀測值。我們將資料集分成訓練集和測試集,以便我們可以使用一組進行訓練,另一組進行測試我們的模型。
# Split the dataset into training and testing sets from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
這裡,X_train 表示訓練資料的輸入特徵,y_train 表示輸出變數(目標變數)。
步驟 2:模型訓練(將簡單線性迴歸擬合到訓練集)
下一步是用訓練資料集擬合我們的模型。我們將使用 scikit-learn 的 LinearRegression 類在訓練資料上訓練一個簡單線性迴歸模型。程式碼如下:
from sklearn.linear_model import LinearRegression # Create a linear regression object regressor= LinearRegression() regressor.fit(X_train, y_train)
fit() 方法用於將線性迴歸物件(regressor)擬合到訓練資料。模型學習預測變數 (X_train) 和目標變數 (y_train) 之間的關係。
步驟 3:模型測試
模型訓練完成後,我們可以使用它對測試資料進行預測。程式碼如下:
y_pred = regressor.predict(X_test)
df = pd.DataFrame({'Actual Values':y_test, 'Predicted Values':y_pred})
print(df)
輸出
Actual Values Predicted Values 0 60150.0 54093.648425 1 93940.0 82416.119864 2 57081.0 64478.554619 3 116969.0 115459.003211 4 56957.0 63534.472238 5 121872.0 124899.827024
以上輸出顯示了測試集中薪資的實際值和預測值。
這裡,X_test 表示測試資料的輸入特徵,y_pred 表示預測的輸出變數(目標變數)。
同樣,您可以使用訓練資料測試模型。
y_pred = regressor.predict(X_train)
df = pd.DataFrame({'Real Values':y_test, 'Predicted Values':y_pred})
print(df)
輸出
Real Values Predicted Values 0 57189.0 60702.225094 1 64445.0 55981.813188 2 63218.0 62590.389857 3 122391.0 123011.662261 4 91738.0 89968.778915 5 43525.0 44652.824612 6 61111.0 68254.884145 7 56642.0 53149.566044 8 66029.0 73919.378433 9 83088.0 75807.543195 10 46205.0 38044.247943 11 109431.0 107906.344160 12 98273.0 92801.026059 13 37731.0 39932.412705 14 54445.0 55981.813188 15 39891.0 46540.989374 16 101302.0 100353.685109 17 55794.0 63534.472238 18 81363.0 81472.037483 19 39343.0 36156.083180 20 113812.0 103185.932253 21 67938.0 72031.213670 22 112635.0 116403.085592 23 105582.0 110738.591304
步驟 4:模型評估
我們需要評估模型的效能以確定其準確性。我們將使用均方誤差 (MSE)、均方根誤差 (RMSE)、平均絕對誤差 (MAE) 和決定係數 (R^2) 作為評估指標。程式碼如下:
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import r2_score
# get the predicted values for test dat
y_pred = regressor.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print("mse", mse)
rmse = mean_squared_error(y_test, y_pred, squared=False)
print("rsme", rmse)
mae = mean_absolute_error(y_test, y_pred)
print("mae", mae)
r2 = r2_score(y_test, y_pred)
print("r2", r2)
輸出
mse: 46485664.99327367 rsme: 6818.0396737826095 mae: 6015.513730219523 r2: 0.9399326805390613
這裡,y_test 表示測試資料的實際輸出變數。
步驟 5:視覺化訓練集結果(帶回歸線)
現在,讓我們視覺化訓練集上的結果和迴歸線。
我們使用散點圖繪製訓練集中實際值(輸入和目標值)。我們還繪製了一條直線(迴歸線)表示訓練集的實際值(輸入)和預測值。
y_pred = regressor.predict(X_train)
plt.scatter(X_train, y_train, color="green", label="training data points (actual)")
plt.scatter(X_train, y_pred, color="blue",label="training data points (predicted)")
plt.plot(X_train, y_pred, color="red")
plt.title("Salary vs Experience (Training Dataset)")
plt.xlabel("Years of Experience")
plt.ylabel("Salary(In Rupees)")
plt.legend()
plt.show()
輸出

上圖顯示了迴歸線(紅色直線)、實際值(綠色)和訓練集的預測值(藍色)。
步驟 6:視覺化測試集結果(帶回歸線)
現在,讓我們視覺化測試集上的結果和迴歸線。
我們使用散點圖繪製測試集中實際值(輸入和目標值)。我們還繪製了一條直線(迴歸線)表示測試集的實際值(輸入)和預測值。
y_pred = regressor.predict(X_test)
plt.scatter(X_test, y_test, color="green", label="test data points (actual)")
plt.scatter(X_test, y_pred, color="blue",label="test data points (predicted)")
plt.plot(X_test, y_pred, color="red")
plt.title("Salary vs Experience (Test Dataset)")
plt.xlabel("Years of Experience")
plt.ylabel("Salary(In Rupees)")
plt.legend()
plt.show()
輸出
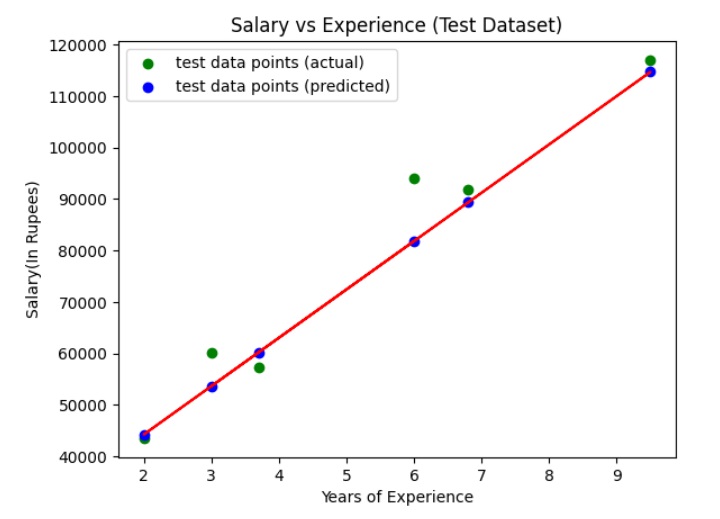
上圖顯示了迴歸線(紅色直線)、實際值(綠色)和測試集的預測值(藍色)。