機器學習 - OPTICS 聚類

OPTICS 類似於 DBSCAN（基於密度的噪聲應用空間聚類），另一種流行的基於密度的聚類演算法。但是，OPTICS 比 DBSCAN 具有幾個優勢，包括能夠識別不同密度的聚類、能夠處理噪聲以及能夠生成層次聚類結構。

在 Python 中實現 OPTICS

為了在 Python 中實現 OPTICS 聚類，我們可以使用 scikit-learn 庫。scikit-learn 庫提供了一個名為 OPTICS 的類，它實現了 OPTICS 演算法。

以下是如何在 scikit-learn 中使用 OPTICS 類對資料集進行聚類的示例：

示例

from sklearn.cluster import OPTICS
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# Generate sample data
X, y = make_blobs(n_samples=2000, centers=4, cluster_std=0.60, random_state=0)

# Cluster the data using OPTICS
optics = OPTICS(min_samples=50, xi=.05)
optics.fit(X)

# Plot the results
labels = optics.labels_
plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='turbo')
plt.show()

在此示例中，我們首先使用 **scikit-learn** 中的 make_blobs 函式生成一個樣本資料集。然後，我們例項化一個 OPTICS 物件，並將 **min_samples** 引數設定為 50，並將 xi 引數設定為 0.05。**min_samples** 引數指定形成聚類所需的最小樣本數，**xi** 引數控制聚類層次結構的陡峭程度。然後，我們使用 fit 方法將 OPTICS 物件擬合到資料集。最後，我們使用散點圖繪製結果，其中每個資料點根據其聚類標籤著色。

輸出

執行此程式時，它將生成以下繪圖作為輸出：

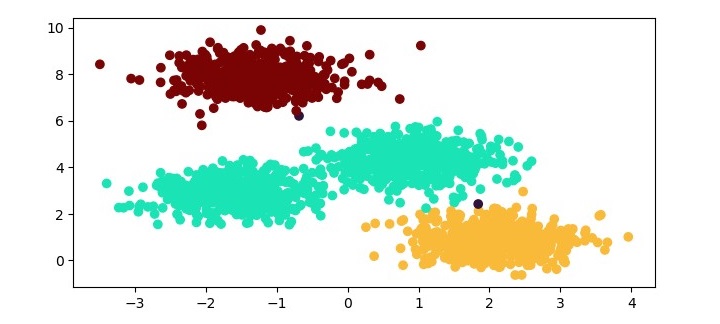
OPTICS 聚類的優勢

以下是使用 OPTICS 聚類的優勢：

• 能夠處理不同密度的聚類 - 與其他一些需要聚類具有均勻密度的聚類演算法不同，OPTICS 可以處理具有不同密度的聚類。

• 能夠處理噪聲 - OPTICS 可以識別不屬於任何聚類的噪聲資料點，這對於從資料集中去除異常值很有用。

• 層次聚類結構 - OPTICS 生成一個層次聚類結構，可用於在不同粒度級別分析資料集。

OPTICS 聚類的缺點

以下是使用 OPTICS 聚類的一些缺點。

• 對引數敏感 - OPTICS 需要仔細調整其引數，例如 min_samples 和 xi 引數，這可能具有挑戰性。

• 計算複雜度 - 對於大型資料集，OPTICS 的計算成本可能很高，尤其是在使用高 min_samples 值時。