機器學習 - K均值聚類

---

---

K均值演算法可以概括為以下步驟：

• 初始化 - 選擇 K 個隨機資料點作為初始中心點。

• 分配 - 將每個資料點分配到最近的中心點。

• 重新計算 - 透過取每個簇中所有資料點的平均值來重新計算中心點。

• 重複 - 重複步驟 2-3，直到中心點不再移動或達到最大迭代次數。

K均值演算法是一種簡單高效的演算法，可以處理大型資料集。但是，它也有一些侷限性，例如它對初始中心點的敏感性、它傾向於收斂到區域性最優解，以及它假設所有簇的方差相等。

Python 實現

Python 有幾個庫提供了各種機器學習演算法的實現，包括 K均值聚類。讓我們看看如何使用 scikit-learn 庫在 Python 中實現 K均值演算法。

步驟 1 - 匯入所需庫

要在 Python 中實現 K均值演算法，我們首先需要匯入所需的庫。我們將分別使用 numpy 和 matplotlib 庫進行資料處理和視覺化，以及 scikit-learn 庫用於 K均值演算法。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

步驟 2 - 生成資料

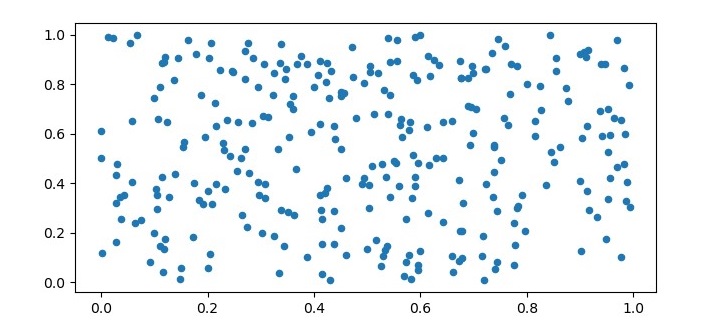
為了測試 K均值演算法，我們需要生成一些示例資料。在本例中，我們將生成 300 個具有兩個特徵的隨機資料點。我們也將視覺化資料。

X = np.random.rand(300,2)

plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:, 0], X[:, 1], s=20, cmap='summer');
plt.show()

步驟 3 - 初始化 K均值

接下來，我們需要透過指定簇數 (K) 和最大迭代次數來初始化 K均值演算法。

kmeans = KMeans(n_clusters=3, max_iter=100)

步驟 4 - 訓練模型

初始化 K均值演算法後，我們可以透過將資料擬合到演算法中來訓練模型。

kmeans.fit(X)

步驟 5 - 視覺化簇

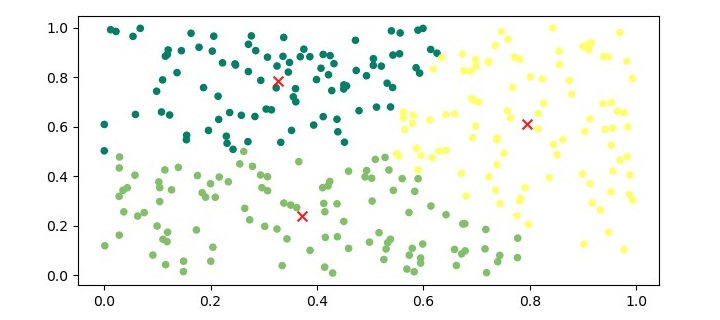
為了視覺化簇，我們可以繪製資料點並根據其分配的簇對其進行著色。

plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:,0], X[:,1], c=kmeans.labels_, s=20, cmap='summer')
plt.scatter(kmeans.cluster_centers_[:,0], kmeans.cluster_centers_[:,1],
marker='x', c='r', s=50, alpha=0.9)
plt.show()

上述程式碼的輸出將是一個圖，其中資料點根據其分配的簇著色，並且中心點以紅色“x”符號標記。

完整實現示例

以下是 Python 中 K均值聚類演算法的完整實現示例：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

X = np.random.rand(300,2)
plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:, 0], X[:, 1], s=20, cmap='summer');
plt.show()

kmeans = KMeans(n_clusters=3, max_iter=100)
kmeans.fit(X)
plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:,0], X[:,1], c=kmeans.labels_, s=20, cmap='summer')
plt.scatter(kmeans.cluster_centers_[:,0], kmeans.cluster_centers_[:,1],
marker='x', c='r', s=50, alpha=0.9)
plt.show()

輸出

執行此程式碼時，它將生成以下圖作為輸出：

K均值聚類的應用

K均值聚類是一種用途廣泛的演算法，在多個領域都有各種應用。在這裡，我們重點介紹了一些重要的應用：

影像分割

K均值聚類可用於根據畫素的顏色或紋理將影像分割成不同的區域。此技術廣泛應用於計算機視覺應用中，例如物體識別、影像檢索和醫學影像。

客戶細分

K均值聚類可用於根據客戶的購買行為或人口統計特徵將客戶細分成不同的群體。此技術廣泛應用於營銷應用中，例如客戶留存、忠誠度計劃和目標廣告。

異常檢測

K均值聚類可用於透過識別不屬於任何簇的資料點來檢測資料集中是否存在異常。此技術廣泛應用於欺詐檢測、網路入侵檢測和預測性維護。

基因組資料分析

K均值聚類可用於分析基因表達資料，以識別不同組的共同調控或共同表達的基因。此技術廣泛應用於生物資訊學應用中，例如藥物發現、疾病診斷和個性化醫療。