
- 機器學習基礎
- ML - 首頁
- ML - 簡介
- ML - 入門
- ML - 基本概念
- ML - 生態系統
- ML - Python庫
- ML - 應用
- ML - 生命週期
- ML - 必備技能
- ML - 實現
- ML - 挑戰與常見問題
- ML - 侷限性
- ML - 真實案例
- ML - 資料結構
- ML - 數學基礎
- ML - 人工智慧
- ML - 神經網路
- ML - 深度學習
- ML - 獲取資料集
- ML - 分類資料
- ML - 資料載入
- ML - 資料理解
- ML - 資料準備
- ML - 模型
- ML - 監督學習
- ML - 無監督學習
- ML - 半監督學習
- ML - 強化學習
- ML - 監督學習 vs. 無監督學習
- 機器學習資料視覺化
- ML - 資料視覺化
- ML - 直方圖
- ML - 密度圖
- ML - 箱線圖
- ML - 相關矩陣圖
- ML - 散點矩陣圖
- 機器學習統計學
- ML - 統計學
- ML - 均值、中位數、眾數
- ML - 標準差
- ML - 百分位數
- ML - 資料分佈
- ML - 偏度和峰度
- ML - 偏差和方差
- ML - 假設
- ML中的迴歸分析
- ML - 迴歸分析
- ML - 線性迴歸
- ML - 簡單線性迴歸
- ML - 多元線性迴歸
- ML - 多項式迴歸
- ML中的分類演算法
- ML - 分類演算法
- ML - 邏輯迴歸
- ML - K近鄰演算法 (KNN)
- ML - 樸素貝葉斯演算法
- ML - 決策樹演算法
- ML - 支援向量機
- ML - 隨機森林
- ML - 混淆矩陣
- ML - 隨機梯度下降
- ML中的聚類演算法
- ML - 聚類演算法
- ML - 基於質心的聚類
- ML - K均值聚類
- ML - K中心點聚類
- ML - 均值漂移聚類
- ML - 層次聚類
- ML - 基於密度的聚類
- ML - DBSCAN聚類
- ML - OPTICS聚類
- ML - HDBSCAN聚類
- ML - BIRCH聚類
- ML - 親和傳播
- ML - 基於分佈的聚類
- ML - 凝聚層次聚類
- ML中的降維
- ML - 降維
- ML - 特徵選擇
- ML - 特徵提取
- ML - 後向剔除法
- ML - 前向特徵構建
- ML - 高相關性過濾器
- ML - 低方差過濾器
- ML - 缺失值比率
- ML - 主成分分析
- 強化學習
- ML - 強化學習演算法
- ML - 利用與探索
- ML - Q學習
- ML - REINFORCE演算法
- ML - SARSA強化學習
- ML - 演員評論家方法
- 深度強化學習
- ML - 深度強化學習
- 量子機器學習
- ML - 量子機器學習
- ML - 使用Python的量子機器學習
- 機器學習雜項
- ML - 效能指標
- ML - 自動化工作流
- ML - 提升模型效能
- ML - 梯度提升
- ML - 自舉匯聚 (Bagging)
- ML - 交叉驗證
- ML - AUC-ROC曲線
- ML - 網格搜尋
- ML - 資料縮放
- ML - 訓練和測試
- ML - 關聯規則
- ML - Apriori演算法
- ML - 高斯判別分析
- ML - 成本函式
- ML - 貝葉斯定理
- ML - 精確率和召回率
- ML - 對抗性
- ML - 堆疊
- ML - 輪次
- ML - 感知器
- ML - 正則化
- ML - 過擬合
- ML - P值
- ML - 熵
- ML - MLOps
- ML - 資料洩露
- ML - 機器學習的貨幣化
- ML - 資料型別
- 機器學習資源
- ML - 快速指南
- ML - 速查表
- ML - 面試問題
- ML - 有用資源
- ML - 討論
機器學習中的線性迴歸
機器學習中的線性迴歸被定義為一種統計模型,它分析因變數與一組給定的自變數之間的線性關係。變數之間的線性關係意味著,當一個或多個自變數的值發生變化(增加或減少)時,因變數的值也會相應地發生變化(增加或減少)。
在機器學習中,線性迴歸用於根據學習到的線性關係來預測新資料和未見資料的連續數值。它被用於預測建模、金融預測、風險評估等。
在本章中,我們將詳細討論以下主題:
- 什麼是線性迴歸?
- 線性迴歸的型別
- 線性迴歸是如何工作的?
- 線性迴歸的假設函式
- 尋找最佳擬合線
- 線性迴歸的損失函式
- 用於最佳化的梯度下降法
- 線性迴歸的假設
- 線性迴歸的評估指標
- 線性迴歸的應用
- 線性迴歸的優點
- 線性迴歸的常見挑戰
什麼是線性迴歸?
線性迴歸是一種統計技術,它估計因變數和一個或多個自變數之間的線性關係。在機器學習中,線性迴歸被實現為一種監督學習方法。在機器學習中,標記資料集包含輸入資料(特徵)和輸出標籤(目標值)。對於機器學習中的線性迴歸,我們將特徵表示為自變數,目標值表示為因變數。
為簡化起見,請考慮以下資料(單個特徵和單個目標):
| 平方英尺 (X) | 房價 (Y) |
|---|---|
| 1300 | 240 |
| 1500 | 320 |
| 1700 | 330 |
| 1830 | 295 |
| 1550 | 256 |
| 2350 | 409 |
| 1450 | 319 |
在上述資料中,目標房價是由 X 表示的因變數,而特徵平方英尺是由 Y 表示的自變數。輸入特徵 (X) 用於預測目標標籤 (Y)。因此,自變數也稱為預測變數,因變數也稱為響應變數。
因此,讓我們將機器學習中的線性迴歸定義如下:
在機器學習中,線性迴歸使用線性方程來模擬因變數 (Y) 和一個或多個自變數 (Y) 之間的關係。
線性迴歸模型的主要目標是找到透過一組資料點的最佳擬合直線(通常稱為迴歸線)。
迴歸線
顯示因變數和自變數之間關係的直線稱為迴歸線。

此外,線性關係可以是正的或負的,如下所述:
1. 正線性關係
如果自變數和因變數都增加,則線性關係稱為正線性關係。這可以透過下圖來理解:

2. 負線性關係
如果自變數增加而因變數減少,則線性關係稱為負線性關係。這可以透過下圖來理解:

線性迴歸分為兩種型別:“簡單線性迴歸”和“多元線性迴歸”,我們將在本教程的接下來的兩章中討論。
線性迴歸的型別
線性迴歸分為以下兩種型別:
- 簡單線性迴歸
- 多元線性迴歸
1. 簡單線性迴歸
簡單線性迴歸是一種迴歸分析,其中使用單個自變數(也稱為預測變數)來預測因變數。換句話說,它模擬因變數和單個自變數之間的線性關係。
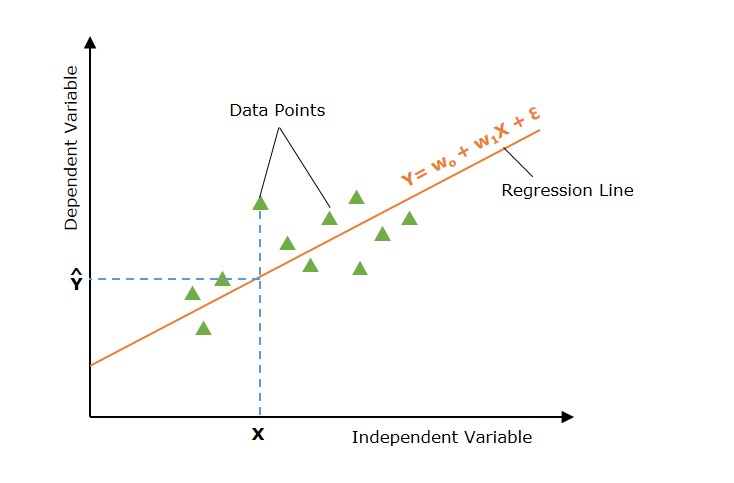
在上圖中,直線代表簡單線性迴歸線,其中 Ŷ 是預測值,X 是輸入值。
數學上,這種關係可以建模為線性方程:
$$\mathrm{ Y = w_0 + w_1 X + \epsilon }$$
其中
- Y 是因變數(目標)。
- X 是自變數(特徵)。
- w0 是線的 y 截距。
- w1 是線的斜率,表示 X 對 Y 的影響。
- ε 是誤差項,捕獲 X 未解釋的 Y 中的可變性。
2. 多元線性迴歸
多元線性迴歸基本上是簡單線性迴歸的擴充套件,它使用兩個或多個特徵來預測響應。
當處理多個自變數時,我們將簡單線性迴歸擴充套件到多元線性迴歸。模型表示為:
多元線性迴歸將簡單線性迴歸的概念擴充套件到多個自變數。模型表示為:
$$\mathrm{Y = w_0 + w_1 X_1 + w_2 X_2 + \dots + w_p X_p + \epsilon}$$
其中
- X1、X2、…、Xp 是自變數(特徵)。
- w0、w1、…、wp 是這些變數的係數。
- ε 是誤差項。
線性迴歸是如何工作的?
線性迴歸的主要目標是找到透過一組資料點的最佳擬合線,使實際值和預測值之間的差異最小化。那麼這是如何實現的呢?這是透過估計引數 w0、w1 等來實現的。
機器學習中線性迴歸的工作原理可以分解為以下步驟:
- **假設** - 我們假設輸入和輸出之間存線上性關係。
- **成本函式** - 定義損失或成本函式。成本函式量化模型的預測誤差。成本函式獲取模型的預測值和實際值,並返回表示模型預測成本的單個標量值。
- **最佳化** - 透過更新模型的引數來最佳化(最小化)模型的成本函式。
它持續更新模型的引數,直到模型預測的成本或誤差被最佳化(最小化)。
讓我們更詳細地討論以上三個步驟 -
線性迴歸的假設函式
線上性迴歸問題中,我們假設輸入特徵 (X) 和預測值 (Ŷ) 之間存線上性關係。
該假設函式返回給定輸入值的預測值。通常我們用 hw(X) 表示假設函式,它等於Ŷ。
簡單線性迴歸的假設函式 -
$$\mathrm{\hat{Y} = w_0 + w_1 X}$$
多元線性迴歸的假設函式 -
$$\mathrm{\hat{Y} = w_0 + w_1 X_1 + w_2 X_2 + \dots + w_p X_p}$$
對於不同的引數值(權重),我們可以找到許多回歸線。主要目標是找到最佳擬合線。讓我們如下討論 -
尋找最佳擬合線
我們在上面討論過,不同的引數集會提供不同的迴歸線。但是,每條迴歸線都不能代表輸入和輸出值之間的最佳關係。主要目標是找到最佳擬合線。
如果實際值和預測值之間的誤差最小,則稱迴歸線為最佳擬合線。
下圖顯示了在輸入資料點 X 處帶有誤差 (ε) 的迴歸線。誤差是針對所有資料點計算的,我們的目標是最小化平均誤差/損失。我們可以使用不同型別的損失函式,例如均方誤差 (MSE)、平均絕對誤差 (MAE)、L1 損失、L2 損失等。
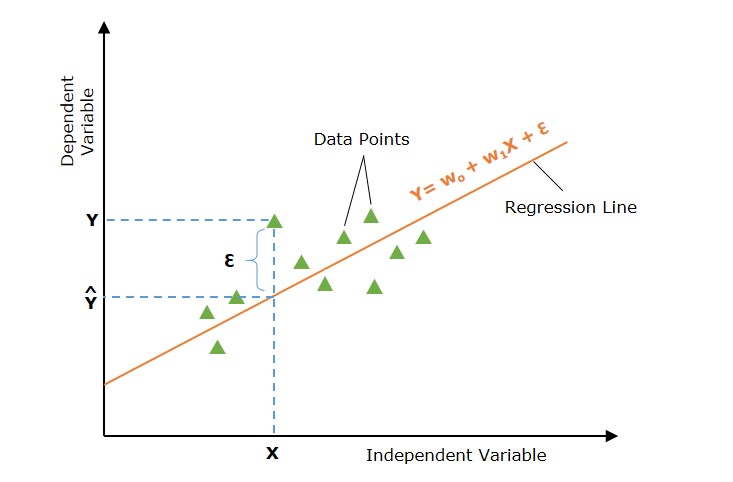
那麼,我們如何最小化實際值和預測值之間的誤差呢?讓我們討論一個重要的概念,即成本函式或損失函式。
線性迴歸的損失函式
可以使用損失函式或成本函式來量化實際值和預測值之間的誤差。該成本函式採用模型的預測值和實際值,並返回一個表示模型預測成本的單個標量值。我們的主要目標是最小化成本函式。
最常用的成本函式是均方誤差函式。
$$\mathrm{J(w_0, w_1) = \frac{1}{2n} \sum_{i=1}^{n} \left( Y_i - \hat{Y}_i \right)^2}$$
其中,
- n 是資料點的數量。
- Yi 是第 i 個數據點的觀測值。
- \( \hat{Y}_i = w_0 + w_1 X_i \) 是第 i 個數據點的預測值。
用於最佳化的梯度下降法
現在我們已經定義了損失函式。下一步是最小化它並找到引數或權重的最優值。找到引數的最優值以使損失或誤差最小化的過程稱為模型最佳化。
梯度下降是線性迴歸最常用的最佳化技術之一。
為了找到引數的最優值,經常使用梯度下降法,尤其是在資料集很大的情況下。梯度下降法迭代地調整引數,使其沿成本函式最陡峭下降的方向移動。
引數更新由下式給出
$$\mathrm{w_0 = w_0 - \alpha \frac{\partial J}{\partial w_0}}$$
$$\mathrm{w_1 = w_1 - \alpha \frac{\partial J}{\partial w_1}}$$
其中 α 是學習率,偏導數為
$$\mathrm{\frac{\partial J}{\partial w_0} = -\frac{1}{n} \sum_{i=1}^{n} \left( Y_i - \hat{Y}_i \right)}$$
$$\mathrm{\frac{\partial J}{\partial w_1} = -\frac{1}{n} \sum_{i=1}^{n} \left( Y_i - \hat{Y}_i \right) X_i}$$
這些梯度用於更新引數,直到達到收斂(即,當 \( w_0 \) 和 \( w_1 \) 的變化變得可以忽略不計)。
線性迴歸的假設
以下是線性迴歸模型對資料集做出的某些假設 -
多重共線性 - 線性迴歸模型假設資料中幾乎沒有或沒有多重共線性。基本上,當自變數或特徵之間存在依賴關係時,就會發生多重共線性。
自相關 - 線性迴歸模型的另一個假設是資料中幾乎沒有或沒有自相關。基本上,當殘差誤差之間存在依賴關係時,就會發生自相關。
變數之間的關係 - 線性迴歸模型假設響應變數和特徵變數之間的關係必須是線性的。
違反這些假設會導致偏差或效率低下的估計。必須驗證這些假設以確保模型的準確性。
線性迴歸的評估指標
為了評估線性迴歸模型的效能,使用了幾個評估指標 -
R 平方 (R2) - 它衡量因變數中可由自變數預測的方差比例。
$$\mathrm{ R^2 = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \bar{y})^2} }$$
均方誤差 (MSE) - 它衡量預測值和實際值之間平方差之和的平均值。
$$\mathrm{ \text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2 }$$
均方根誤差 (RMSE) - 它衡量 MSE 的平方根。
$$\mathrm{ \text{RMSE} = \sqrt{\text{MSE}} }$$
平均絕對誤差 (MAE) - 它衡量預測值和實際值之間差異的絕對值之和的平均值。
$$\mathrm{ \text{MAE} = \frac{1}{n} \sum_{i=1}^n |y_i - \hat{y}_i| }$$
線性迴歸的應用
1. 預測建模
線性迴歸廣泛用於預測建模。例如,在房地產中,根據大小、位置和臥室數量等特徵預測房價可以幫助買家、賣家和房地產經紀人做出明智的決定。
2. 特徵選擇
在多元線性迴歸中,分析係數有助於特徵選擇。係數較小或為零的特徵可能被認為不太重要,可以刪除以簡化模型。
3. 金融預測
在金融領域,線性迴歸模型可以預測股票價格、經濟指標和市場趨勢。準確的預測可以指導投資策略和財務規劃。
4. 風險管理
線性迴歸透過對風險因素和財務指標之間的關係建模來幫助進行風險評估。例如,在保險中,它可以對投保人特徵與索賠金額之間的關係建模。
線性迴歸的優點
- 可解釋性 - 線性迴歸易於理解,這在解釋模型如何做出決策時非常有用。
- 速度 - 線性迴歸比許多其他機器學習演算法訓練速度更快。
- 預測分析 - 線性迴歸是預測分析的基礎組成部分。
- 線性關係 - 線性迴歸是一種強大的統計方法,用於查詢變數之間的線性關係。
- 簡單性 - 線性迴歸易於實現和解釋。
- 效率 - 線性迴歸計算效率高。
線性迴歸的常見挑戰
1. 過擬合
過擬合是指回歸模型在訓練資料上表現良好,但在測試資料上缺乏泛化能力的情況。過擬合會導致對新的、未見過的資料的預測效果差。
2. 多重共線性
當因變數(預測變數或特徵變數)相關時,這種情況稱為多重共線性。在這種情況下,引數(係數)的估計值可能不穩定。
3. 離群值及其影響
離群值會導致迴歸線成為大多數資料點的糟糕擬合。
多項式迴歸:線性迴歸的替代方法
多項式線性迴歸是一種迴歸分析,其中自變數和因變數之間的關係被建模為 n 次多項式函式。多項式迴歸允許捕獲變數之間比簡單和多元線性迴歸中的線性關係更復雜的關係。