直流電動機的工作原理

直流電動機的工作原理基於電磁相互作用定律。根據該定律，當載流導體或線圈置於磁場中時，導體或線圈會受到電磁力。

此力的幅度由下式給出：

$$\mathrm{\mathit{F=BIL}}$$

其中：

• $\mathit{B}$ 為磁通密度，

• $\mathit{I}$ 為流過導體或線圈的電流，以及

• $\mathit{l}$ 為導體的長度。

此力的方向可以透過弗萊明左手定則 (FLHR)確定，我們在本教程的模組 1（基本概念）中討論過。

為了理解直流電動機的工作原理，考慮圖 1 所示的雙極直流電動機。

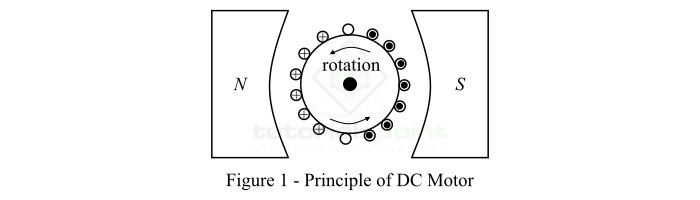
當該直流電動機的端子連線到外部直流電源時，機器內部會發生以下兩種現象：

• 勵磁電磁鐵被激磁，產生交替的N極和S極。

• 電樞導體帶有電流。其中，N極下的導體電流方向相同（例如，指向紙內），而S極下的導體電流方向相反（例如，指向紙外）。

由於在這種情況下，每個導體都帶有電流並置於磁場中。由於電流和磁場之間的相互作用，導體上會作用一個機械力。

應用弗萊明左手定則，可以清楚地看出，每個導體上的機械力都傾向於使導體沿逆時針方向移動。所有導體上的機械力加在一起產生一個驅動轉矩，使電樞旋轉。

當導體從一個極側移動到另一個極側時，由於換向作用，該導體中的電流反向，同時，它受到下一個極性相反的極的影響。結果，導體上力的方向保持不變。透過這種方式，直流電動機的電樞持續在一個方向上旋轉。

直流電動機的電樞轉矩

直流電動機的電樞繞其軸旋轉。因此，作用於電樞上的機械力稱為電樞轉矩。它定義為作用於電樞導體上的力的轉動矩，由下式給出：

$$\mathrm{\mathit{\tau _{a}}/conductor\:=\:\mathit{F\times r}}$$

其中，F 是作用在每個導體上的力，r 是電樞的平均半徑。

如果電樞中的導體數為 Z，則總電樞轉矩由下式給出：

$$\mathrm{\therefore \mathit{\tau _{a}}\:=\:\mathit{ZF\times r}\:=\:\mathit{ZBIL\times r}}$$

因為

$$\mathrm{\mathit{B}\:=\:\frac{\mathit{\phi }}{\mathit{a}};\:\mathit{I\:=\:\frac{I_{a}}{A}};\mathit{a\:=\:\frac{\mathrm{2}\pi rl}{P}}}$$

其中，$\phi$ 為每極磁通量，$\mathit{I_{a}}$ 為電樞電流，l 為每個電樞導體的有效長度，A 為並聯支路數，P 為極數。然後，

$$\mathrm{\mathit{\tau _{a}}\:=\:\frac{\mathit{Z\phi I_{a}}P}{\mathrm{2}\pi A}}$$

因為對於給定的直流電動機，Z、P 和 A 是固定的。

$$\mathrm{\therefore \mathit{\tau _{a}}\propto \mathit{\phi I_{a}}}$$

因此，直流電動機的轉矩與每極磁通量和電樞電流成正比。