三相感應電動機的特性

三相感應電機的執行效能可以用以下兩個特性來解釋：

• 轉矩-滑差特性

• 轉矩-速度特性

三相感應電機的轉矩-滑差特性

三相感應電機的**轉矩-滑差特性**是電機轉矩和滑差在特定轉子電阻值下繪製的曲線。圖1顯示了典型三相感應電機在滑差範圍為s = 0到s = 1的不同轉子電阻值下的不同轉矩-滑差特性。

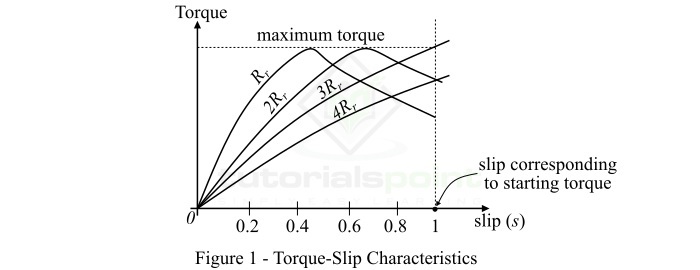
對於三相感應電機，執行條件下電機轉矩和滑差之間的關係由下式給出：

$$ \mathrm{\mathit{\tau _{r}}\:=\:\frac{\mathit{KsR_{r}}}{\mathit{R_{r}^{\mathrm{2}}+s^{\mathrm{2}}X_{r}^{\mathrm{2}}}}\:\cdot \cdot \cdot (1)} $$

其中，**K** 是常數，s 是滑差，$\mathit{R_{r}}$ 是每相轉子電阻，$\mathit{X_{r}}$ 是每相靜止轉子電抗。

從公式1，我們可以得出以下幾點：

情況1

如果s = 0，則$\mathit{\tau _{r}}\:=\:0$。因此，轉矩-滑差曲線從原點開始。

情況2

在電機的正常速度下，滑差很小，因此$\mathit{sX_{r}}$與$\mathit{R_{r}}$相比可以忽略不計。

$$ \mathrm{\therefore \mathit{\tau _{r}}\propto \mathit{\frac{s}{R_{r}}}} $$

由於對於給定的電機，$\mathit{R_{r}}$也是常數。

$$ \mathrm{\therefore \mathit{\tau _{r}}\propto \mathit{s}} $$

因此，轉矩-滑差曲線是從零滑差到對應於滿載滑差的直線。

情況3

如果滑差值超過滿載滑差，則轉矩增加，當$\mathit{R _{r}}\:=\:\mathit{s\:X_{r}}$時達到最大值。三相感應電機中的這個最大轉矩稱為**擊穿轉矩**或**拉出轉矩**。當感應電機在額定電壓和頻率下執行時，擊穿轉矩的值至少是滿載轉矩的兩倍。

情況4

當滑差值大於對應於最大轉矩的滑差值時，$\mathit{s^{\mathrm{2}}\:X_{r}^{\mathrm{2}}}$項迅速增加，因此$\mathit{R_{r}^{\mathrm{2}}}$可以忽略不計。

$$ \mathrm{\therefore \mathit{\tau _{r}}\propto \mathit{\frac{s}{s^{\mathrm{2}}X_{r}^{\mathrm{2}}}}} $$

由於$\mathit{X_{r}^{\mathrm{2}}}$實際上是常數，則

$$ \mathrm{\mathit{\tau _{r}}\propto \mathit{\frac{\mathrm{1}}{s}}} $$

因此，轉矩現在與滑差成反比。因此，轉矩-滑差曲線是矩形雙曲線。

因此，從以上對三相感應電機轉矩-滑差特性的分析可以看出，向轉子電路增加電阻不會改變最大轉矩的值，而只會改變發生最大轉矩的滑差值。

三相感應電機的轉矩-速度特性

對於三相感應電機，電機轉矩取決於速度，但我們不能用簡單的數學方程來表達它們之間的關係。因此，我們使用轉矩-速度特性曲線來顯示這種關係。圖2顯示了三相感應電機的典型轉矩-速度特性曲線。

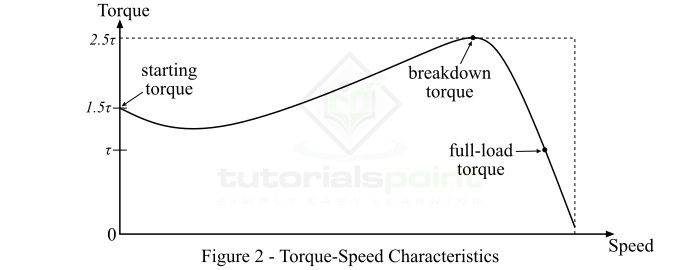
從該特性曲線可以看出以下幾點：

• 如果滿載轉矩為$\tau$，則啟動轉矩為$1.5\tau$，最大轉矩（或擊穿轉矩）為$2.5\tau$

• 在滿載情況下，如果電機的速度為N，如果軸上的機械負載增加，電機的速度將下降，直到電機轉矩再次等於負載轉矩。一旦兩個轉矩相等，電機將以恆定速度執行，但低於之前的速度。然而，如果電機轉矩大於$2.5\tau$（即擊穿轉矩），電機將突然停止。

• 對於三相感應電機，轉矩-速度曲線在空載和滿載點之間基本上是一條直線。曲線線的斜率取決於轉子電路的電阻，即電阻越大，斜率越陡。