單激發和雙激發系統

---

---

勵磁是指向機電能量轉換裝置（如電動機）提供電輸入。勵磁在電機中產生工作磁場。一些電機需要單個電輸入，而另一些則需要兩個電輸入。

因此，根據機電能量轉換系統的電輸入數量，可以將其分為兩種型別：

• 單激發系統

• 雙激發系統

單激發系統

顧名思義，單激發系統只有一個通電線圈來在機器或任何其他機電能量轉換裝置中產生工作磁場。因此，單激發系統只需要一個電輸入。

單激發系統由繞在磁芯上的線圈組成，並連線到電壓源，以便產生磁場。由於這個磁場，由鐵磁材料製成的轉子（或運動部件）會受到一個力矩的作用，使其朝著磁場更強的區域移動，即作用在轉子上的力矩試圖將其定位，使其在磁通路徑中表現出最小的磁阻。磁阻取決於轉子角度。這個力矩被稱為磁阻轉矩或凸極轉矩，因為它是由轉子的凸極引起的。

單激發系統的分析

我們做了以下假設來分析單激發系統：

• 對於任何轉子位置，磁鏈 ($\psi$) 和電流 ($\mathit{i}$) 之間的關係是線性的。

• 線圈的漏磁通可忽略不計，這意味著所有磁通都流過主磁路。

• 忽略滯後損耗和渦流損耗。

• 所有電場都被忽略，磁場占主導地位。

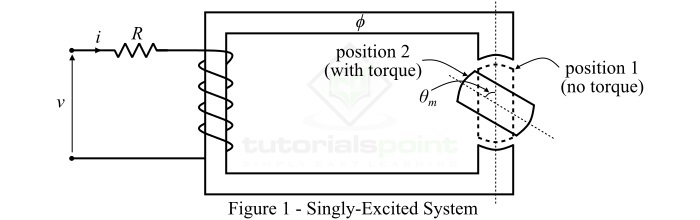
考慮如圖1所示的單激發系統。如果R是線圈電路的電阻，則透過應用KVL，我們可以將電壓方程寫為：

$$\mathrm{\mathit{v\:=\:iR\:+\:\frac{\mathit{d\psi }}{\mathit{dt}}}\cdot \cdot \cdot (1)}$$

用電流$\mathit{i}$乘以方程(1)，我們有：

$$\mathrm{\mathit{vi\:=\:i^{\mathrm{2}}R\:+\mathit{i}\:\frac{\mathit{d\psi }}{\mathit{dt}}}\cdot \cdot \cdot (2)}$$

我們假設系統的初始條件為零，並在兩邊對方程(2)關於時間積分，我們得到：

$$\mathrm{\int_{0}^{\mathit{T}}\mathit{vi\:dt}\:=\:\int_{0}^{\mathit{T}}\left ( i^{\mathrm{2}}\mathit{R}\:+\mathit{i}\:\frac{\mathit{d\psi }}{\mathit{dt}} \right )\mathit{dt}}$$

$$\mathrm{\Rightarrow\int_{0}^{\mathit{T}}\mathit{vi\:dt}\:=\:\int_{0}^{\mathit{T}}\mathit{i^{\mathrm{2}}R\:dt}\:+\:\int_{0}^{\psi }\mathit{i\:d\psi }\cdot \cdot \cdot (3)}$$

方程-3給出了單激發系統的總電能輸入，它等於兩部分：

• 第一部分是電損耗 ($\mathit{W_{el}}$)。

• 第二部分是有用電能，它是磁場能量 ($\mathit{W_{f}}$) 和輸出機械能 ($\mathit{W_{m}}$) 的總和。

因此，我們可以象徵性地將方程-3表示為：

$$\mathrm{\mathit{W_{in}}\:=\:\mathit{W_{el}}\:=\:\left (\mathit{W_{f}} \:+\:\mathit{W_{m}} \right )}\cdot \cdot \cdot (4)$$

單激發系統儲存在磁場中的能量由下式給出：

$$\mathrm{\mathit{W_{f}}\:=\: \int_{0}^{\psi }\mathit{i\:d\psi }\:=\:\int_{0}^{\psi }\frac{\psi }{\mathit{L}}\mathit{d\psi }\:=\:\frac{\psi ^{\mathrm{2}}}{2\mathit{L}}\cdot \cdot \cdot (5)}$$

對於轉子運動，其中轉子角度為$\mathit{\theta _{m}}$，單激發系統產生的電磁轉矩由下式給出：

$$\mathrm{\mathit{\tau _{e}}\:=\:\frac{\mathit{i^{\mathrm{2}}}}{\mathrm{2}}\frac{\mathit{\partial L}}{\mathit{\partial \theta _{m}}}\cdot \cdot \cdot (6)}$$

單激發系統最常見的例子是感應電機、PMMC儀表等。

雙激發系統

具有兩個獨立線圈來產生磁場的電磁系統被稱為雙激發系統。因此，雙激發系統需要兩個獨立的電輸入。

雙激發系統的分析

雙激發系統主要由定子和轉子兩部分組成，如圖2所示。這裡，定子繞組有一個電阻為R₁的線圈，轉子繞組有一個電阻為R₂的線圈。因此，有兩個獨立的繞組，它們由兩個獨立的電壓源激磁。

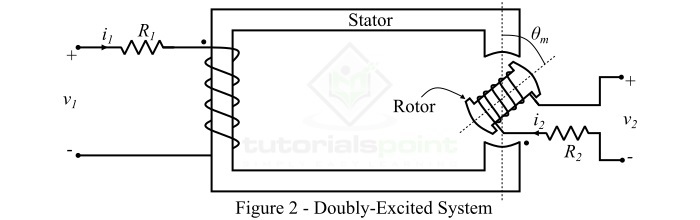
為了分析雙激發系統，做了以下假設：

• 對於任何轉子位置，磁鏈 ($\psi$) 和電流之間的關係是線性的。

• 忽略滯後損耗和渦流損耗。

• 線圈的漏磁通可忽略不計。

• 電場被忽略，磁場占主導地位。

兩個繞組的磁通鏈分別為：

$$\mathrm{\psi _{\mathrm{1}}\:=\:\mathit{L_{\mathrm{1}}i_{\mathrm{1}}}\:+\:\mathit{Mi_{\mathrm{2}}}}\cdot \cdot \cdot (7)$$

$$\mathrm{\psi _{\mathrm{2}}\:=\:\mathit{L_{\mathrm{2}}i_{\mathrm{2}}}\:+\:\mathit{Mi_{\mathrm{2}}}}\cdot \cdot \cdot (8)$$

其中，M是兩個繞組之間的互感。

透過應用KVL，我們可以將兩個線圈的瞬時電壓方程寫為：

$$\mathrm{\mathit{v}_{\mathrm{1}}\:=\:\mathit{i_{\mathrm{1}}R_{\mathrm{1}}}\:+\:\frac{\mathit{d\psi _{\mathrm{1}}}}{\mathit{dt}}}\cdot \cdot \cdot (9)$$

$$\mathrm{\mathit{v}_{\mathrm{2}}\:=\:\mathit{i_{\mathrm{2}}R_{\mathrm{2}}}\:+\:\frac{\mathit{d\psi _{\mathrm{2}}}}{\mathit{dt}}}\cdot \cdot \cdot (10)$$

在雙激發系統中，儲存在磁場中的能量由下式給出：

$$\mathrm{\mathit{W_{f}}\:=\:\frac{1}{2}\mathit{L_{\mathrm{1}}i_{\mathrm{1}}^{\mathrm{2}}}\:+\:\frac{1}{2}\mathit{L_{\mathrm{2}}i_{\mathrm{2}}^{\mathrm{2}}}\:+\:\mathit{Mi_{\mathrm{1}}i_{\mathrm{2}}}\cdot \cdot \cdot (11)}$$

並且，雙激發系統產生的電磁轉矩由下式給出：

$$\mathrm{\mathit{\tau _{e}}\:=\:\frac{\mathit{i_{\mathrm{1}}^{\mathrm{2}}}}{\mathrm{2}}\frac{\mathit{dL_{\mathrm{1}}}}{\mathit{d\theta _{m}}}\:+\:\frac{\mathit{i_{\mathrm{2}}^{\mathrm{2}}}}{\mathrm{2}}\frac{\mathit{dL_{\mathrm{2}}}}{\mathit{d\theta _{m}}}\:+\:\mathit{i_{\mathrm{1}}i_{\mathrm{2}}}\frac{\mathit{dM}}{\mathit{d\theta _{m}}}\cdot \cdot \cdot (12)}$$

在方程-12中，前兩項是磁阻轉矩，最後一項是由於兩個磁場的相互作用而產生的同軸轉矩。

雙激發系統的實際例子是同步電機、測速機、他勵直流電機等。