理想變壓器與實際變壓器

---

---

理想變壓器

理想變壓器是一個想象中的變壓器模型，它具有以下特徵：

• 初級和次級繞組的電阻可以忽略不計（或為零）。

• 沒有漏磁通，即所有磁通都流過變壓器的鐵芯。

• 鐵芯具有無限的磁導率，這意味著建立鐵芯磁通所需的磁動勢可以忽略不計。

• 沒有由於繞組電阻、磁滯和渦流引起的損耗。因此，它的效率為100%。

理想變壓器的原理

我們可以分析理想變壓器在空載或負載下的工作情況，這將在以下部分進行討論。

理想變壓器空載工作

考慮一個空載的理想變壓器，即其次級繞組開路，如圖1所示。並且，初級繞組是一個純電感線圈。

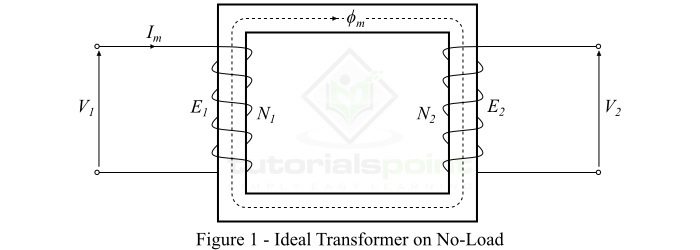
當一個交流電壓$\mathit{V_{\mathrm{1}}}$施加到初級繞組時，它會吸取一個非常小的勵磁電流$\mathit{I_{\mathit{m}}}$來建立鐵芯中的磁通，該磁通滯後於施加電壓90°。勵磁電流Im在鐵芯中產生一個與之成正比且同相位的交變磁通$\mathit{\phi_{m}}$。這個交變磁通($\mathit{\phi_{m}}$)透過磁耦合方式連線初級和次級繞組，並在初級繞組中感應出電動勢$\mathit{E_{\mathrm{1}}}$，並在次級繞組中感應出電動勢$\mathit{E_{\mathrm{2}}}$。

初級繞組中感應的電動勢$\mathit{E_{\mathrm{1}}}$等於並與施加電壓$\mathit{V_{\mathrm{1}}}$相反（根據楞次定律）。電動勢$\mathit{E_{\mathrm{1}}}$和$\mathit{E_{\mathrm{2}}}$滯後於磁通($\mathit{\phi_{m}}$)90°，但是它們的幅值取決於初級和次級繞組的匝數。此外，電動勢$\mathit{E_{\mathrm{1}}}$和$\mathit{E_{\mathrm{2}}}$彼此同相，而$\mathit{E_{\mathrm{1}}}$等於$\mathit{V_{\mathrm{1}}}$並與其反相180°。

理想變壓器負載工作

當一個負載連線到理想變壓器次級繞組的端子上時，則稱變壓器處於負載狀態，負載電流流過次級繞組和負載。

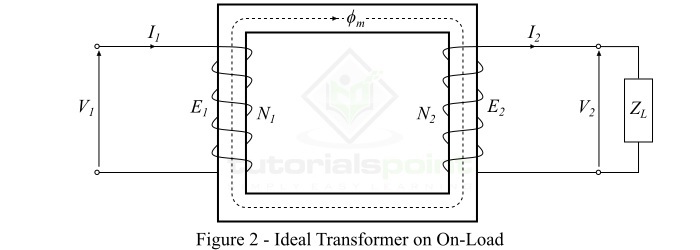
考慮一個阻抗為Z_L的感性負載連線到理想變壓器的次級繞組上，如圖2所示。然後，次級繞組電動勢$\mathit{E_{\mathrm{2}}}$將導致電流$\mathit{I_{\mathrm{2}}}$流過次級繞組和負載，該電流由下式給出：

$$\mathrm{\mathit{I_{\mathrm{2}}}\:=\:\frac{\mathit{E_{\mathrm{2}}}}{\mathit{Z_{\mathit{L}}}}\:=\:\frac{\mathit{V_{\mathrm{2}}}}{\mathit{Z_{\mathit{L}}}}}$$

其中，對於理想變壓器，次級繞組電動勢$\mathit{E_{\mathrm{2}}}$等於次級繞組端電壓$\mathit{V_{\mathrm{2}}}$。

由於我們考慮的是感性負載，因此，電流$\mathit{I_{\mathrm{2}}}$將滯後於$\mathit{E_{\mathrm{2}}}$或$\mathit{V_{\mathrm{2}}}$一個角度$\mathit{\phi_{\mathrm{2}}}$。此外，由於變壓器是理想變壓器，因此忽略空載電流$\mathit{I_{\mathrm{0}}}$。

流過次級繞組的電流($\mathit{I_{\mathrm{2}}}$)會建立一個磁動勢($\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}$)，該磁動勢產生一個與主磁通($\mathit{\phi_{\mathit{m}}}$)方向相反的磁通$\mathit{\phi_{\mathrm{2}}}$。結果，鐵芯中的總磁通量與其原始值發生變化，但是鐵芯中的磁通量不應該偏離其原始值。因此，為了使鐵芯中的磁通量保持其原始值，初級電流必須產生一個磁動勢來抵消次級磁動勢$\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}$的退磁作用。

因此，初級電流$\mathit{I_{\mathrm{1}}}$必須流動，以便

$$\mathrm{\mathit{I_{\mathrm{1}}}\mathit{N_{\mathrm{1}}}\:=\:\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}}$$

因此，初級繞組必須吸取足夠的電流來抵消次級電流的退磁作用，以使鐵芯中的主磁通保持恆定。因此，當次級電流($\mathit{I_{\mathrm{2}}}$)增加時，初級電流($\mathit{I_{\mathrm{1}}}$)也以相同的方式增加，並使互磁通($\mathit{\phi_{\mathit{m}}}$)保持恆定。

在負載下的理想變壓器中，次級電流$\mathit{I_{\mathrm{2}}}$滯後於次級端電壓$\mathit{V_{\mathrm{2}}}$一個角度$\mathit{\phi _{\mathrm{2}}}$。

實際變壓器

實際變壓器具有以下特徵：

• 初級和次級繞組具有有限的電阻。

• 存在漏磁通，即並非所有磁通都侷限於鐵芯。

• 鐵芯具有有限的磁導率，因此需要相當數量的磁動勢來建立鐵芯磁通。

• 由於繞組電阻、磁滯和渦流，變壓器中存在損耗。因此，實際變壓器的效率始終小於100%。

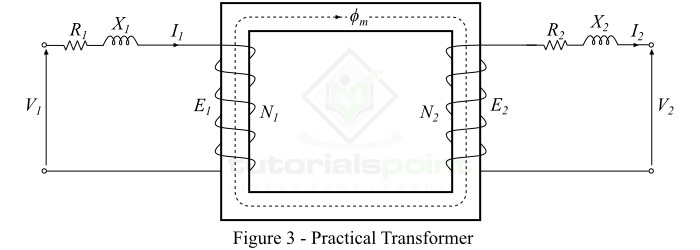
典型實際變壓器的分析模型如圖3所示。

實際變壓器的特性

以下是實際變壓器的主要特性：

繞組電阻

變壓器的繞組通常由銅導體組成。因此，初級和次級繞組都將具有繞組電阻，這會在變壓器中產生銅損或$\mathit{i^{\mathrm{2}} \mathit{R}}$損耗。初級繞組電阻$\mathit{R_{\mathrm{1}}}$和次級繞組電阻$\mathit{R_{\mathrm{2}}}$分別與各自的繞組串聯，如圖3所示。

鐵損或鐵芯損耗

變壓器的鐵芯承受交變磁通，因此鐵芯中會產生渦流損耗和磁滯損耗。磁滯損耗和渦流損耗統稱為鐵損或鐵芯損耗。變壓器的鐵損取決於電源頻率、鐵芯中的最大磁通密度、鐵芯體積和疊片厚度等。在實際變壓器中，鐵損的幅值實際上是恆定的且非常小。

漏磁通

初級繞組中的電流產生磁通。連線初級和次級繞組的磁通$\mathit{\phi _{\mathit{m}}}$是有用磁通，稱為互磁通。但是，初級電流產生的部分磁通($\mathit{\phi _{\mathrm{1}}}$)不會與次級繞組連線。

當負載連線到次級繞組時，電流流過它併產生磁通($\mathit{\phi _{\mathrm{2}}}$)，該磁通僅與次級繞組連線。因此，$\mathit{\phi _{\mathrm{1}}}$的一部分和僅與其各自繞組連線的磁通$\mathit{\phi _{\mathrm{2}}}$稱為漏磁通。

漏磁通的路徑是空氣，空氣具有非常高的磁阻。因此，初級漏磁通($\mathit{\phi _{\mathrm{1}}}$)的作用是在初級繞組中引入一個與之串聯的感抗($ \mathit{X_{\mathrm{1}}}$)。類似地，次級漏磁通($\mathit{\phi _{\mathrm{2}}}$)在次級繞組中引入一個與之串聯的感抗($ \mathit{X_{\mathrm{2}}}$)，如圖3所示。

但是，實際變壓器中的漏磁通非常小（約佔$\mathit{\phi _{m}}$的5%），但不能忽略。因為漏磁通路徑是空氣，空氣具有非常高的磁阻。因此，它需要相當大的磁動勢。

鐵芯材料的有限磁導率

通常，實際變壓器的鐵芯由高等級矽鋼製成，它具有特定的相對磁導率($\mathit{\mu _{r}}$)。因此，鐵芯在某個磁通密度值下會飽和。因此，實際變壓器的鐵芯具有有限的磁導率，因此在磁通路徑中具有磁阻。