
- 電機教程
- 電機 - 首頁
- 基本概念
- 機電能量轉換
- 儲存在磁場中的能量
- 單激發和雙激發系統
- 旋轉電機
- 法拉第電磁感應定律
- 感應電動勢的概念
- 弗萊明左手定則和右手定則
- 變壓器
- 電力變壓器
- 變壓器的構造
- 變壓器的電動勢方程
- 變壓比和電壓變換比
- 理想變壓器和實際變壓器
- 直流變壓器
- 變壓器的損耗
- 變壓器的效率
- 三相變壓器
- 變壓器的型別
- 直流電機
- 直流電機的構造
- 直流電機的型別
- 直流發電機的原理
- 直流發電機的電動勢方程
- 直流發電機的型別
- 直流電機的原理
- 直流電機中的反電動勢
- 直流電機的型別
- 直流電機的損耗
- 直流電機的應用
- 感應電機
- 感應電機的介紹
- 單相感應電機
- 三相感應電機
- 三相感應電機的構造
- 三相感應電機負載執行
- 三相感應電機的特性
- 調速和速度控制
- 三相感應電機的啟動方法
- 同步電機
- 三相同步電機的介紹
- 同步電機的構造
- 三相交流發電機的執行原理
- 同步電機中的電樞反應
- 三相交流發電機的輸出功率
- 三相交流發電機的損耗和效率
- 三相同步電機的執行原理
- 同步電機的等效電路和功率因數
- 同步電機產生的功率
- 電機資源
- 電機快速指南
- 電機 - 資源
- 電機 - 討論
電機快速指南
機電能量轉換
如今,電能是應用最廣泛的一種能量形式,用於執行各種工業、商業和家用功能,例如抽水、風扇、冷卻器、空調、製冷等。由於大多數工藝都需要將電能轉換為機械能,同時機械能也轉換為電能。因此,我們需要一種機制來將電能轉換為機械能,並將機械能轉換為電能,這種機制被稱為機電能量轉換裝置。
機電能量轉換裝置
因此,能夠將電能轉換為機械能或將機械能轉換為電能的裝置稱為機電能量轉換裝置。電動發電機和電動機是機電能量轉換裝置的例子。
在任何機電能量轉換裝置中,電能與機械能的相互轉換都是透過電場或磁場作為媒介進行的。然而,在大多數實際的機電能量轉換裝置中,磁場用作電氣系統和機械系統之間的耦合介質。
機電能量轉換裝置可分為兩類:
大運動裝置(如電機和發電機)
增量運動裝置(如電磁繼電器、測量儀器、揚聲器等)
將電能轉換為機械能的裝置稱為電動機。將機械能轉換為電能的裝置稱為發電機。
在電動機中,當載流導體置於變化的(或旋轉的)磁場中時,導體會受到機械力。在發電機的情況下,當導體在磁場中運動時,導體中會感應出電動勢。儘管這兩種電磁效應同時發生,但能量轉換在所有機電能量轉換裝置中都是從電能到機械能,反之亦然。
能量平衡方程
能量平衡方程是一個表示式,它顯示了能量轉換的完整過程。在機電能量轉換裝置中,總輸入能量等於三個分量的總和:
能量耗散或損失
儲存的能量
有用輸出能量
因此,對於電動機,能量平衡方程可以寫成:
Electrical energy input = Energy dissipated + Energy stored + Mechanical energy output
其中:
電能輸入是從主電源提供的電力。
儲存的能量等於儲存在磁場中的能量以及以勢能和動能形式儲存在機械系統中的能量之和。
能量耗散等於電阻損耗、磁芯損耗(磁滯損耗+渦流損耗)和機械損耗(風損和摩擦損耗)之和。
對於發電機,能量平衡方程可以寫成:
Mechanical energy input = Electrical energy output + Energy stored + Energy dissipated
其中,機械能輸入是從渦輪機、發動機等獲得的機械能,用於旋轉發電機的軸。
儲存在磁場中的能量
在上一章中,我們討論了在機電能量轉換裝置中,電氣系統和機械系統之間存在耦合介質。在大多數實際裝置中,磁場用作耦合介質。因此,機電能量轉換裝置包括一個電磁系統。因此,儲存在耦合介質中的能量是以磁場的形式存在的。我們可以計算如下所述的機電能量轉換系統的磁場中儲存的能量。
考慮一個具有 *N* 個導線匝數的線圈繞在一個磁芯上,如圖 1 所示。該線圈由 *v* 伏特的電壓源供電。
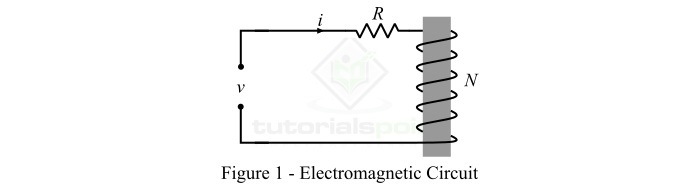
透過應用基爾霍夫電壓定律 (KVL),施加到線圈的電壓由下式給出:
$$\mathrm{\mathit{V\:=\:e\:+\:iR}\cdot \cdot \cdot (1)}$$
其中:
e 是由於電磁感應而線上圈中感應的電動勢。
R 是線圈電路的電阻。
$\mathit{i}$ 是流過線圈的電流。
電磁系統的瞬時功率輸入由下式給出:
$$\mathrm{\mathit{p}\:=\:\mathit{Vi\:=\:i\left ( e+iR \right )}}$$
$$\mathrm{\Rightarrow \mathit{p}\:=\:\mathit{ie+ i^{\mathrm{2}}}\mathit{R}\cdot \cdot \cdot (2)}$$
現在,假設在時間 *t* = 0 時將直流電壓施加到電路,並在時間 *t* = *t1* 秒結束時,電路中的電流達到 *I* 安培。然後,在此時間間隔內,系統輸入的能量由下式給出:
$$\mathrm{\mathit{W}_{in}\:=\:\int_{0}^{t_{\mathrm{1}}}\:\mathit{p\:dt}}$$
$$\mathrm{\Rightarrow \mathit{W}_{in}\:=\:\int_{0}^{t_{\mathrm{1}}}\:\mathit{ie\:dt}\:+\:\int_{0}^{t_{\mathrm{1}}}\mathit{i^{\mathrm{2}}R\:dt}\cdot \cdot \cdot (3)}$$
從公式 3 可以看出,總輸入能量由兩部分組成:
第一部分是儲存在磁場中的能量。
第二部分是由於線圈的電阻而耗散的能量。
因此,儲存在系統磁場中的能量為:
$$\mathrm{\mathit{W}_{\mathit{f}}\:=\:\int_{0}^{t_{\mathrm{1}}}\:\mathit{ie\:dt}\:\cdot \cdot \cdot (4)}$$
根據法拉第電磁感應定律,我們有:
$$\mathrm{\mathit{e}\:=\:\frac{\mathit{d\psi }}{\mathit{dt}}\:=\:\frac{\mathit{d}}{\mathit{dt}}\left ( \mathit{N\phi } \right )\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}\cdot \cdot \cdot (5)}$$
其中,$\psi$ 是磁通鏈,等於 $\mathit{\psi \:=\:N\phi }$.
$$\mathrm{\therefore \mathit{W_{f}}\:=\:\int_{0}^{\mathit{t_{\mathrm{1}}}}\frac{\mathit{d\psi }}{\mathit{dt}}\mathit{i\:dt}}$$
$$\mathrm{\Rightarrow \mathit{W_{f}}\:=\:\int_{0}^{\psi_{\mathrm{1}}}\mathit{i\:d\psi }\cdot \cdot \cdot (6)}$$
因此,公式 (6) 表明,儲存在磁場中的能量等於電磁系統的 ($\psi -i$) 曲線(即磁化曲線)與磁通鏈 ($\psi$) 軸之間的面積,如圖 2 所示。
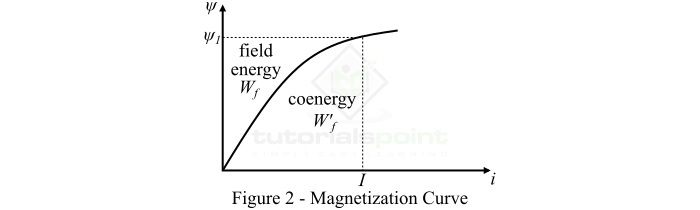
對於線性電磁系統,儲存在磁場中的能量由下式給出:
$$\mathrm{\mathit{W_{f}}\:=\:\int_{0}^{\mathit{\psi _{\mathrm{1}}}}\mathit{id\psi }\:=\:\int_{0}^{\psi_{\mathrm{1}} }\frac{\psi }{\mathit{L}}\mathit{d\psi }}$$
其中,$\psi\:=\:\mathit{N\phi }\:=\:\mathit{Li}$,*L* 是線圈的自感。
$$\mathrm{\therefore \mathit{W_{f}}\:=\:\frac{\psi ^{\mathrm{2}}}{2\mathit{L}}\:=\:\frac{1}{2}\mathit{Li^{\mathrm{2}}}\cdot \cdot \cdot (7)}$$
餘能的概念
餘能是一個虛構的概念,用於推導電磁系統中產生的轉矩表示式。因此,餘能在系統中沒有物理意義。
基本上,餘能是 $\psi -i$ 曲線與電流軸之間的面積,表示為 $\mathit{W_{f}^{'}}$,如上圖 2 所示。
在數學上,餘能由下式給出:
$$\mathrm{\mathit{W_{f}^{'}}\:=\:\int_{0}^{i}\psi \mathit{di}\:=\:\int_{0}^{i}\mathit{Li\:di}}$$
$$\mathrm{\Rightarrow \mathit{W_{f}^{'}}\:=\:\frac{1}{2}\mathit{Li^{\mathrm{2}}}\cdot \cdot \cdot (8)}$$
從公式 (7) 和 (8) 可以看出,對於線性磁系統,儲存在磁場中的能量和餘能是相等的。
單激發和雙激發系統
勵磁是指向機電能量轉換裝置(例如電動機)提供電能輸入。勵磁在電機中產生工作磁場。有些電機需要單一的電能輸入,而有些電機需要兩個電能輸入。
因此,根據機電能量轉換系統的電能輸入數量,它們可以分為兩種型別:
單激發系統
雙激發系統
單激發系統
顧名思義,單激發系統只有一個通電線圈來在機器或任何其他機電能量轉換裝置中產生工作磁場。因此,單激發系統只需要一個電能輸入。
單激發系統由繞在磁芯上的線圈組成,並連線到電壓源,以便產生磁場。由於這個磁場,由鐵磁材料製成的轉子(或運動部分)會受到一個力矩,該力矩將其移動到磁場更強的區域,即作用在轉子上的力矩試圖將其定位,使其在磁通路徑中顯示最小的磁阻。磁阻取決於轉子角度。這個力矩稱為磁阻轉矩或凸極轉矩,因為它是由轉子的凸極引起的。
單激發系統的分析
我們做了以下假設來分析單激發系統:
對於任何轉子位置,磁通鏈 ($\psi$) 和電流 ($\mathit{i}$) 之間的關係是線性的。
線圈的漏磁通可忽略不計,這意味著所有磁通都流經主磁路。
忽略磁滯損耗和渦流損耗。
所有電場都被忽略,磁場占主導地位。
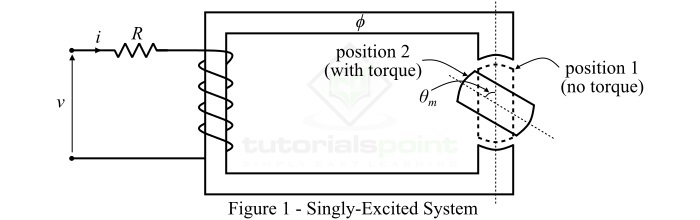
考慮如圖 1 所示的單激發系統。如果 *R* 是線圈電路的電阻,則透過應用 KVL,我們可以將電壓方程寫成:
$$\mathrm{\mathit{v\:=\:iR\:+\:\frac{\mathit{d\psi }}{\mathit{dt}}}\cdot \cdot \cdot (1)}$$
將公式 (1) 乘以電流 $\mathit{i}$,我們得到:
$$\mathrm{\mathit{vi\:=\:i^{\mathrm{2}}R\:+\mathit{i}\:\frac{\mathit{d\psi }}{\mathit{dt}}}\cdot \cdot \cdot (2)}$$
我們假設系統的初始條件為零,並在兩邊對公式 (2) 關於時間積分,我們得到:
$$\mathrm{\int_{0}^{\mathit{T}}\mathit{vi\:dt}\:=\:\int_{0}^{\mathit{T}}\left ( i^{\mathrm{2}}\mathit{R}\:+\mathit{i}\:\frac{\mathit{d\psi }}{\mathit{dt}} \right )\mathit{dt}}$$
$$\mathrm{\Rightarrow\int_{0}^{\mathit{T}}\mathit{vi\:dt}\:=\:\int_{0}^{\mathit{T}}\mathit{i^{\mathrm{2}}R\:dt}\:+\:\int_{0}^{\psi }\mathit{i\:d\psi }\cdot \cdot \cdot (3)}$$
公式 3 給出了單激發系統的總電能輸入,它等於兩部分,即:
第一部分是電損耗 ($\mathit{W_{el}}$)。
第二部分是有用電能,它是磁場能量 ($\mathit{W_{f}}$) 和輸出機械能 ($\mathit{W_{m}}$) 之和。
因此,我們可以用符號表示公式 3 為:
$$\mathrm{\mathit{W_{in}}\:=\:\mathit{W_{el}}\:=\:\left (\mathit{W_{f}} \:+\:\mathit{W_{m}} \right )}\cdot \cdot \cdot (4)$$
單激勵系統的磁場儲存能量由下式給出:
$$ \mathrm{\mathit{W_{f}}\:=\: \int_{0}^{\psi }\mathit{i\:d\psi }\:=\:\int_{0}^{\psi }\frac{\psi }{\mathit{L}}\mathit{d\psi }\:=\:\frac{\psi ^{\mathrm{2}}}{2\mathit{L}}\cdot \cdot \cdot (5)} $$
對於轉子運動,其中轉子角度為$\mathit{\theta _{m}}$,單激勵系統中產生的電磁轉矩由下式給出:
$$ \mathrm{\mathit{\tau _{e}}\:=\:\frac{\mathit{i^{\mathrm{2}}}}{\mathrm{2}}\frac{\mathit{\partial L}}{\mathit{\partial \theta _{m}}}\cdot \cdot \cdot (6)} $$
單激勵系統最常見的例子包括感應電機、PMMC儀表等。
雙激勵系統
具有兩個獨立線圈來產生磁場的電磁系統被稱為雙激勵系統。因此,雙激勵系統需要兩個獨立的電輸入。
雙激勵系統的分析
雙激勵系統由兩個主要部分組成,即定子和轉子,如圖2所示。這裡,定子繞組具有電阻R1,轉子繞組具有電阻R2。因此,有兩個獨立的繞組,由兩個獨立的電壓源激勵。
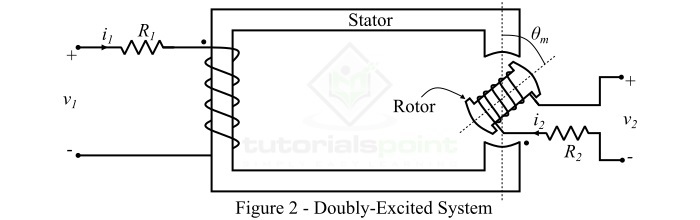
為了分析雙激勵系統,做出以下假設:
對於任何轉子位置,磁鏈 ($\psi$) 和電流之間的關係都是線性的。
忽略滯後和渦流損耗。
線圈的漏磁可忽略不計。
忽略電場,磁場占主導地位。
兩個繞組的磁通鏈由下式給出:
$$ \mathrm{\psi _{\mathrm{1}}\:=\:\mathit{L_{\mathrm{1}}i_{\mathrm{1}}}\:+\:\mathit{Mi_{\mathrm{2}}}}\cdot \cdot \cdot (7) $$
$$ \mathrm{\psi _{\mathrm{2}}\:=\:\mathit{L_{\mathrm{2}}i_{\mathrm{2}}}\:+\:\mathit{Mi_{\mathrm{2}}}}\cdot \cdot \cdot (8) $$
其中,M 是兩個繞組之間的互感。
應用基爾霍夫電壓定律,我們可以寫出兩個線圈的瞬時電壓方程:
$$ \mathrm{\mathit{v}_{\mathrm{1}}\:=\:\mathit{i_{\mathrm{1}}R_{\mathrm{1}}}\:+\:\frac{\mathit{d\psi _{\mathrm{1}}}}{\mathit{dt}}}\cdot \cdot \cdot (9) $$
$$ \mathrm{\mathit{v}_{\mathrm{2}}\:=\:\mathit{i_{\mathrm{2}}R_{\mathrm{2}}}\:+\:\frac{\mathit{d\psi _{\mathrm{2}}}}{\mathit{dt}}}\cdot \cdot \cdot (10) $$
在雙激勵系統中,磁場儲存能量由下式給出:
$$ \mathrm{\mathit{W_{f}}\:=\:\frac{1}{2}\mathit{L_{\mathrm{1}}i_{\mathrm{1}}^{\mathrm{2}}}\:+\:\frac{1}{2}\mathit{L_{\mathrm{2}}i_{\mathrm{2}}^{\mathrm{2}}}\:+\:\mathit{Mi_{\mathrm{1}}i_{\mathrm{2}}}\cdot \cdot \cdot (11)} $$
並且,雙激勵系統中產生的電磁轉矩由下式給出:
$$ \mathrm{\mathit{\tau _{e}}\:=\:\frac{\mathit{i_{\mathrm{1}}^{\mathrm{2}}}}{\mathrm{2}}\frac{\mathit{dL_{\mathrm{1}}}}{\mathit{d\theta _{m}}}\:+\:\frac{\mathit{i_{\mathrm{2}}^{\mathrm{2}}}}{\mathrm{2}}\frac{\mathit{dL_{\mathrm{2}}}}{\mathit{d\theta _{m}}}\:+\:\mathit{i_{\mathrm{1}}i_{\mathrm{2}}}\frac{\mathit{dM}}{\mathit{d\theta _{m}}}\cdot \cdot \cdot (12)} $$
在公式(12)中,前兩項是磁阻轉矩,最後一項是由於兩個磁場的相互作用而產生的同軸轉矩。
雙激勵系統的實際例子包括同步電機、測速機、他勵直流電機等。
旋轉電機
幾乎所有電機都具有幾個相似的特性和功能。以下討論將解釋旋轉電機的基本共同特性。其中,旋轉電機是指具有一個運動(旋轉)部分(稱為轉子)的電機。旋轉電機的常見例子包括電動機和發電機。
在旋轉電機中,產生的轉矩可以根據瞬時磁通模式來考慮。根據這一概念,當淨磁場具有不對稱性或畸變時,會在電機中產生轉矩。
在任何旋轉電機中,機械力(轉矩)都是由於以下兩種磁場效應產生的:
磁力線的對準
磁場與載流導體之間的相互作用
在實際電機中,磁場是透過勵磁線圈系統產生的。這是因為這種磁場產生方法相對通用且經濟。
旋轉電機的基本結構
所有旋轉電機的基本結構和構造都是相似的。典型的旋轉電機由兩個主要部分組成,即:
定子
轉子
定子和轉子之間由氣隙隔開。顧名思義,定子是電機的靜止(不可移動)部分。通常,定子是電機的外部框架。轉子是電機的旋轉(可移動)部分。定子和轉子都是使用疊片鐵磁材料製成的,以減少磁通路徑中的磁阻。
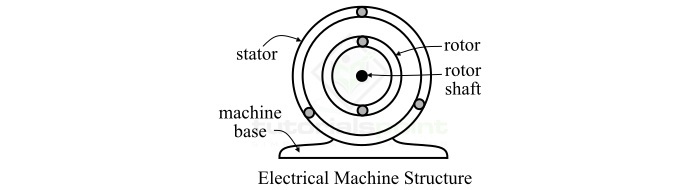
所有旋轉電機都包含兩個繞組,一個放置在定子上,另一個放置在轉子上。在其中感應電壓的電機繞組被稱為電樞繞組。用於在電機中產生主要工作磁通的繞組被稱為勵磁繞組。有時,使用永磁體代替勵磁繞組來產生主要的磁通。
旋轉磁場
由對稱佈置並供以多相電流的繞組(線圈)系統產生的在空間中旋轉的合成磁場稱為旋轉磁場 (RMF)。
旋轉磁場是這樣的,它的磁極不會保持在固定位置,而是不斷地改變其位置。磁場旋轉的速度稱為同步速度,用 NS 表示。同步速度的數學表示式為:
$$ \mathrm{\mathit{N_{s}}\:=\:\frac{120\mathit{f}}{\mathit{P}}} $$
其中,f 是以 Hz 為單位的電源頻率,P 是極數。它以RPM(每分鐘轉數)為單位測量。
電機轉矩
轉矩定義為力的旋轉運動。轉矩是旋轉電機轉子的主要因素。在機電裝置中,產生兩種型別的轉矩:
電磁轉矩
磁阻轉矩
電磁轉矩
電磁轉矩是由兩個可能彼此相對移動的線圈中的電流產生的磁場的相互作用產生的。在旋轉電機中,在正常執行條件下,存在兩個磁場——一個來自定子電路的磁場,另一個來自轉子電路的磁場。這兩個磁場之間的相互作用在電機中產生轉矩。這個轉矩稱為電磁轉矩。電磁轉矩也稱為感應轉矩。
磁阻轉矩
當由鐵磁材料製成的物體置於外部磁場中時,會受到力(轉矩)的作用,使物體與外部磁場對齊,這稱為磁阻轉矩。
磁阻轉矩的產生是因為外部磁場在鐵磁物體中感應出內部磁場,並且兩個磁場的相互作用產生轉矩,使物體移動以與外部磁場對齊。由於磁阻轉矩作用於物體,試圖使物體處於磁通的最小磁阻(或凸極性)位置。因此,磁阻轉矩也稱為對準轉矩或凸極轉矩。
法拉第電磁感應定律
當變化的磁場與導體或線圈連線時,在導體或線圈中會產生電動勢,這種現象稱為電磁感應。電磁感應是設計電機最基本的概念。
英國科學家邁克爾·法拉第進行了幾次實驗來演示電磁感應現象。他將所有實驗的結果總結為兩條定律,俗稱法拉第電磁感應定律。
法拉第第一定律
法拉第電磁感應第一定律提供了關於在導體或線圈中感應電動勢的條件的資訊。第一定律指出:
當與導體或線圈連線的磁通發生變化時,在導體或線圈中就會感應出電動勢。
因此,在導體或線圈中感應電動勢的基本需求是與導體或線圈連線的磁通量的變化。
法拉第第二定律
法拉第電磁感應第二定律給出了導體或線圈中感應電動勢的大小,可以表述如下:
導體或線圈中感應電動勢的大小與磁通鏈隨時間的變化率成正比。
解釋
假設一個線圈有 N 個匝數,並且與線圈連線的磁通量在 t 秒內從 $\mathit{\phi _{\mathrm{1}}}$ 韋伯變為 $\mathit{\phi _{\mathrm{2}}}$ 韋伯。現在,線圈的磁通鏈 ($\mathit{\psi }$) 是磁通量和線圈匝數的乘積。因此,
$$ \mathrm{\mathrm{初始磁通鏈,}\mathit{\psi _{\mathrm{1}}}\:=\:\mathit{N\phi _{\mathrm{1}}}} $$
$$ \mathrm{\mathrm{最終磁通鏈,}\mathit{\psi _{\mathrm{2}}}\:=\:\mathit{N\phi _{\mathrm{2}}}} $$
根據法拉第電磁感應定律,
$$ \mathrm{\mathrm{感應電動勢,}\mathit{e}\propto \frac{\mathit{N\phi _{\mathrm{2}}}-\mathit{N\phi} _{\mathrm{1}}}{\mathit{t}}\cdot \cdot \cdot (1)} $$
$$ \mathrm{\Rightarrow \mathit{e}\:=\:\mathit{k}\left ( \frac{\mathit{N\phi _{\mathrm{2}}}-\mathit{N\phi} _{\mathrm{1}}}{\mathit{t}} \right )} $$
其中,k 是比例常數,在 SI 單位中其值為 1。
因此,線圈中感應的電動勢由下式給出:
$$ \mathrm{\mathit{e}\:=\:\frac{\mathit{N\phi _{\mathrm{2}}}-\mathit{N\phi} _{\mathrm{1}}}{\mathit{t}}\cdot \cdot \cdot (2)} $$
微分形式為:
$$ \mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}\cdot \cdot \cdot (3)} $$
感應電動勢的方向總是使得它傾向於建立一個電流,該電流產生的磁通量會阻礙引起感應電動勢的磁通量變化。因此,線圈中感應電動勢的大小和方向應寫為:
$$ \mathrm{ \mathit{e}\:=\:\mathit{-N}\frac{\mathit{d\phi }}{\mathit{dt}}\cdot \cdot \cdot (4)} $$
其中,負號 (-) 表示感應電動勢的方向使得它阻礙產生它的原因,即磁通量的變化,這個說法被稱為楞次定律。公式 (4) 是楞次定律的數學表示。
感應電動勢的概念
根據電磁感應原理,當與導體或線圈連線的磁通量發生變化時,在導體或線圈中就會感應出電動勢。在實踐中,採用以下兩種方法來改變磁通鏈:
方法 1 - 導體在靜止磁場中運動
我們可以使導體或線圈在靜止磁場中運動,使得與導體或線圈連線的磁通量的大小發生變化。因此,在導體中會感應出電動勢。這種感應電動勢稱為動態感應電動勢。之所以這樣稱呼,是因為它是感應在運動的導體中的電動勢。動態感應電動勢的例子是交流發電機和直流發電機中產生的電動勢。
方法 2 - 靜止導體置於變化的磁場中
當靜止導體或線圈置於運動的或變化的磁場中時,在導體或線圈中就會感應出電動勢。以這種方式感應的電動勢稱為靜態感應電動勢。之所以這樣稱呼,是因為電動勢是感應在靜止的導體中的。變壓器中感應的電動勢是靜態感應電動勢的一個例子。
因此,從上面的討論可以看出,感應電動勢可以分為兩大類:
動態感應電動勢
靜態感應電動勢
動態感應電動勢
如上節所述,動態感應電動勢是在置於靜止磁場中的運動導體或線圈中感應的電動勢。動態感應電動勢的表示式可以如下推導:
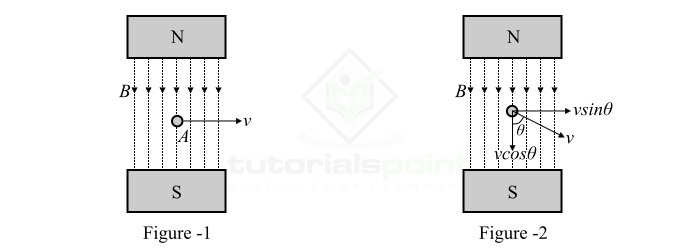
考慮一根長度為l米、位於磁通密度為B Wb/m2的均勻磁場中的單根導體,如圖1所示。該導體以v m/s的速度垂直於磁場運動。
現在,如果導體在dt秒內移動一小段距離dx,則導體掃過的面積為:
$$\mathrm{\mathit{A\:=\:l\times dx\:}\mathrm{m^{\mathrm{2}}}}$$
因此,導體切割的磁通量為:
$$\mathrm{\mathit{d\phi }\:=\:\mathrm{磁通密度\times 掃過面積}}$$
$$\mathrm{\Rightarrow \mathit{d\phi }\:=\:\mathit{B\times l\times dx}\:\mathrm{Wb}}$$
根據法拉第電磁感應定律,導體中感應的電動勢為:
$$\mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}\:=\:\mathit{N}\frac{\mathit{Bldx}}{\mathit{dt}}}$$
由於我們只考慮了一根導體,因此N = 1。
$$\mathrm{\mathit{e}\:=\:\mathit{Blv}\:\mathrm{伏特}\cdot \cdot \cdot (1)}$$
其中,v = dx/dt,為導體在磁場中的速度。
如果導體在磁場中存在角運動,並且導體相對於磁場以θ角移動,如圖2所示。則導體穿過磁場的速度等於“vsinθ”。因此,感應電動勢為:
$$\mathrm{\mathit{e}\:=\:\mathit{B\:l\:v}\:\mathrm{sin\mathit{\theta }}\:\mathrm{伏特}\cdot \cdot \cdot (2)}$$
靜態感應電動勢
當靜止導體置於變化的磁場中時,導體中感應的電動勢稱為**靜電感應電動勢**。靜電感應電動勢進一步分為以下兩種型別:
自感電動勢
互感電動勢
自感電動勢
當由於導體或線圈自身磁通鏈路的改變而在導體或線圈中感應出電動勢時,它被稱為**自感電動勢**。

考慮一個如圖3所示的N匝線圈。流過線圈的電流線上圈中建立磁場。如果線圈中的電流發生變化,則與線圈相關的磁通量也會發生變化。根據法拉第電磁感應定律,這個變化的磁場線上圈中感應出電動勢。這種電動勢稱為自感電動勢,自感電動勢的大小由下式給出:
$$\mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}}$$
互感電動勢
由於相鄰線圈變化的磁場線上圈中感應出的電動勢稱為**互感電動勢**。

考慮兩個線圈X和Y彼此相鄰放置,如圖4所示。這裡,線圈X產生的磁通量的一部分與線圈Y相連。線圈X的這種對線圈X和Y都共有的磁通量稱為**互感磁通量($\mathit{\phi _{m}}$)**。
如果線圈X中的電流發生變化,則互感磁通量也會發生變化,因此線上圈中感應出電動勢。其中,線上圈X中感應的電動勢稱為自感電動勢,線上圈Y中感應的電動勢稱為**互感電動勢**。
根據法拉第定律,互感電動勢的大小由下式給出:
$$\mathrm{\mathit{e_{m}}\:=\:\mathit{N_{Y}}\frac{\mathit{d\phi _{m}}}{\mathit{dt}}}$$
其中,$\mathit{N_{Y}}$是線圈Y的匝數,$\frac{\mathit{d\phi _{m}}}{\mathit{dt}}$是互感磁通量的變化率。
弗萊明左手定則和右手定則
所有電機都基於**電磁感應原理**工作。根據該原理,如果導體和磁場之間存在相對運動,則會在導體中感應出電動勢。另一方面,如果載流導體置於磁場中,則導體會受到力的作用。出於實際和分析的目的,確定導體中感應電動勢的方向和作用在導體上的力的方向非常重要。**弗萊明右手定則**用於此目的。
英國電氣工程師和物理學家**約翰·安布羅斯·弗萊明**在19世紀後期提出了兩條規則,用於確定置於磁場中的載流導體上感應電動勢的方向和作用力。這些規則俗稱**弗萊明左手定則**和**弗萊明右手定則**。
基本上,左手定則和右手定則都顯示了磁場、力和電流之間的關係。
弗萊明左手定則用於確定載流導體在磁場中受到的力的方向,因此主要適用於電動機。而弗萊明右手定則用於確定相對於磁場移動的導體中感應電動勢的方向,因此主要適用於發電機。
弗萊明左手定則
**弗萊明左手定則**特別適用於尋找載流導體在磁場中受力的方向,其陳述如下:
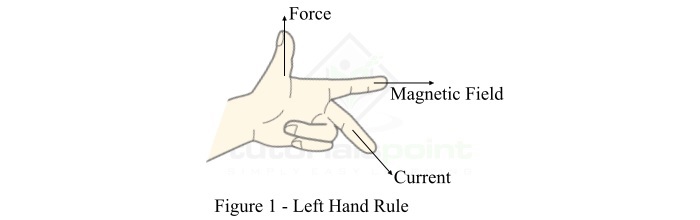
伸出你左手的食指、中指和拇指,使它們相互垂直(如圖1所示)。如果食指指向磁場方向,中指指向導體中電流的方向,則拇指將指向導體上力的方向。
在實踐中,弗萊明左手定則用於確定電動機中導體運動的方向。
弗萊明右手定則
**弗萊明右手定則**特別適用於確定當導體和磁場之間存在相對運動時,導體中感應電動勢的方向以及電流的方向。弗萊明右手定則可以表述如下:
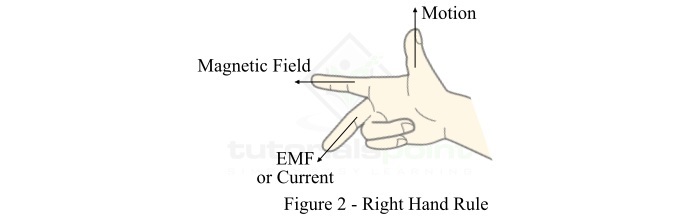
伸出你右手的食指、中指和拇指,使它們相互垂直(如圖2所示)。如果食指指向磁場方向,拇指指向導體運動的方向,則中指將指向感應電動勢或電流的方向。
在實踐中,弗萊明右手定則用於確定發電機中感應電動勢和電流的方向。
弗萊明左手定則和右手定則的比較
下表簡要比較了弗萊明左手定則和右手定則:
| 引數 | 弗萊明左手定則 | 弗萊明右手定則 |
|---|---|---|
| 用途 | 弗萊明左手定則用於確定載流導體在磁場中受力的方向。 | 弗萊明右手定則用於確定導體中感應電動勢或電流的方向。 |
| 應用 | 弗萊明左手定則主要適用於電動機。 | 弗萊明右手定則適用於發電機。 |
電力變壓器
在電力和電子系統中,**電力變壓器**是最有用的電力裝置之一。電力變壓器可以升高或降低交流電壓或電流的大小。這是交流電比直流電廣泛應用的主要原因。變壓器沒有任何移動部件。因此,它的效率非常高,可達99%,結構非常堅固耐用。
電力變壓器
**變壓器**或**電力變壓器**是一種靜態交流電力裝置,它可以在不改變電源頻率的情況下改變交流電壓或交流電流的電平。
典型的變壓器由兩個繞組組成,即**初級繞組**和**次級繞組**。這兩個繞組透過一個公共磁路相互連線,用於在它們之間傳輸電能。
變壓器工作原理
變壓器的工作原理是基於**互感原理**,該原理指出,當一個線圈變化的磁場與另一個線圈相連時,在第二個線圈中會感應出電動勢。

當將交流電壓V1施加到初級繞組時,交流電流流過它併產生交流磁通。這種變化的磁通流過變壓器的鐵芯並與次級繞組相連。根據法拉第電磁感應定律,由於初級繞組變化磁通的連線,在次級繞組中感應出電動勢E2。如果透過連線負載來閉合次級繞組電路,則次級繞組中的感應電動勢E2會導致次級電流I2流過負載。
雖然初級繞組的變化磁通也與初級繞組本身相連。因此,由於其自身的電感效應,在初級繞組中感應出電動勢E1。E1和E2的值可以用以下公式給出:
$$\mathrm{\mathit{E_{\mathrm{1}}}\:=\:-\mathit{N_{\mathrm{1}}}\frac{\mathit{d\phi }}{\mathit{dt}}}$$
$$\mathrm{\mathit{E_{\mathrm{2}}}\:=\:-\mathit{N_{\mathrm{2}}}\frac{\mathit{d\phi }}{\mathit{dt}}}$$
其中N1和N2分別是初級繞組和次級繞組的匝數。
取E2和E1的比率,我們得到:
$$\mathrm{\frac{\mathit{E_{\mathrm{2}}}}{\mathit{E_{\mathrm{1}}}}\:=\:\frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}}}$$
這個表示式稱為變壓器的**變壓比**。變壓比取決於初級和次級繞組的匝數。這意味著輸出電壓的大小取決於初級和次級繞組的相對匝數。
如果N2 > N1,則E2 > E1,即變壓器的輸出電壓大於輸入電壓,這種變壓器稱為**升壓變壓器**。另一方面,如果N1 > N2,則E1 > E2,即輸出電壓小於輸入電壓,這種變壓器稱為**降壓變壓器**。
從變壓器的電路圖中,我們可以看到初級和次級之間沒有電氣連線,而是透過磁場連線。因此,變壓器使我們能夠將交流電能以磁的方式從一個電路轉移到另一個電路,同時改變電壓和電流水平。
要點
注意以下關於變壓器的要點:
變壓器的執行基於電磁感應原理。
變壓器不改變頻率,即輸入電源和輸出電源的頻率保持不變。
變壓器是一種靜態電力裝置,這意味著它沒有任何運動部件。因此,它具有很高的效率。
變壓器不能與直流電一起工作,因為它是一種電磁感應裝置。
原邊和副邊繞組之間沒有直接的電氣連線。交流電透過磁通量從原邊傳輸到副邊。
變壓器的構造
變壓器主要由三個部分組成:原邊繞組、副邊繞組和鐵心。原邊繞組用於輸入電源,副邊繞組用於輸出。鐵心用於將磁通量限制在一定的路徑內。
我們設計的變壓器儘可能接近理想變壓器的特性。在實踐中,我們為變壓器的構造採用了以下設計特點:
變壓器的鐵心由高品質矽鋼製成,具有高磁導率和低磁滯損耗。
鐵心採用疊片結構以最大限度地減少渦流損耗。
通常更有效的方法是在一個鐵芯柱上繞制原邊和副邊繞組的一半,而不是將原邊繞組放在一個鐵芯柱上,副邊繞組放在另一個鐵芯柱上。這樣做可以確保兩個繞組之間緊密的磁耦合,從而大大減少漏磁通。
繞組電阻R1和R2儘可能減小,以使I2R損耗和溫升降至最低,並確保更高的效率。
變壓器結構
變壓器可以透過以下兩種方式構造:
核心式變壓器結構
殼式變壓器結構
核心式變壓器結構
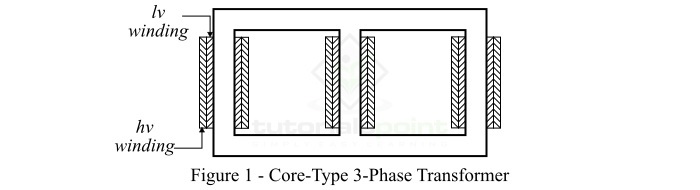
在核心式變壓器的結構中,鐵心有兩個垂直的支柱(稱為鐵芯柱)和兩個水平部分(稱為軛)。原邊繞組的一半和副邊繞組的一半分別繞在每個鐵芯柱上,如圖1所示。
這種繞組佈置最大限度地減少了漏磁通。在實踐中,低壓繞組(可以是原邊或副邊)靠近鐵心放置,高壓繞組繞在低壓繞組周圍。這大大減少了絕緣材料的需求。
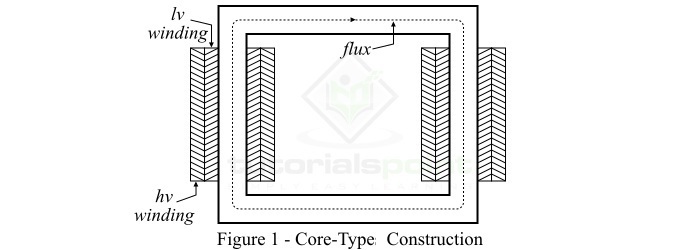
核心式變壓器結構的主要優點是易於拆卸維修。核心式結構最適合高壓大功率變壓器,因為在核心式結構中,自然冷卻效率更高。
殼式變壓器結構
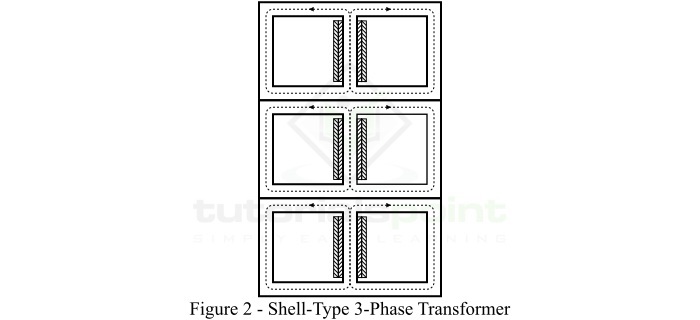
在殼式變壓器的結構中,原邊和副邊繞組都繞在中心鐵芯柱上,而兩個外側鐵芯柱構成低磁阻的磁通路徑,如圖2所示。
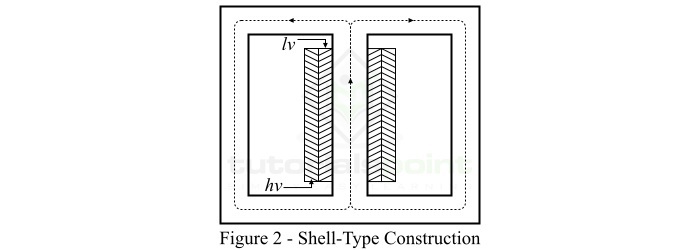
在這種情況下,每個繞組都細分為幾段,低壓(lv)繞組段和高壓(hv)繞組段交替排列成三明治狀。因此,這種型別的繞組也稱為三明治繞組或疊片繞組。
殼式變壓器結構提供了更好的機械支撐,可以抵抗載流繞組之間的電磁力。此外,這種變壓器結構為磁通提供了更短的路徑,因此需要較小的勵磁電流。由於繞組嵌入,殼式結構的自然冷卻效果較差,因此更適用於低壓變壓器。
變壓器的電動勢方程
對於電力變壓器,電動勢方程是用於求解變壓器繞組中感應電動勢大小的數學表示式。
考慮圖中所示的變壓器。如果N1和N2是原邊和副邊繞組的匝數。當我們將頻率為f的交流電壓V1施加到原邊繞組時,原邊繞組在鐵心中產生交變磁通量$\phi$。
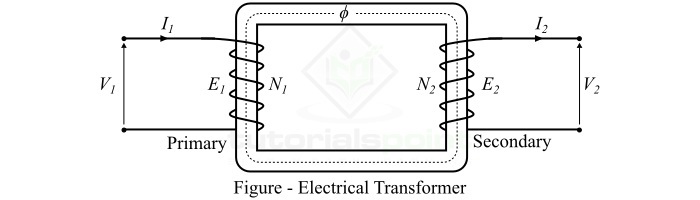
如果我們假設正弦交流電壓,則磁通量可以表示為:
$$\mathrm{\mathit{\phi }\:=\:\phi _{m}\:\mathrm{sin}\:\mathit{\omega t}\:\cdot \cdot \cdot (1)}$$
現在,根據電磁感應原理,原邊繞組中感應電動勢e1的瞬時值由下式給出:
$$\mathrm{\mathit{e_{\mathrm{1}}}\:=\:\mathit{-N_{\mathrm{1}}}\frac{\mathit{d\phi }}{\mathit{dt}}}$$
$$\mathrm{\Rightarrow \mathit{e_{\mathrm{1}}}\:=\:\mathit{-N_{\mathrm{1}}}\frac{\mathit{d}}{\mathit{dt}}\left ( \phi _{m}\: \mathrm{sin}\:\mathit{\omega t}\right )}$$
$$\mathrm{\Rightarrow \mathit{e_{\mathrm{1}}}\:=\:\mathit{-N_{\mathrm{1}}}\:\mathit{\omega \phi \:cos\:\omega t}}$$
$$\mathrm{\Rightarrow \mathit{e_{\mathrm{1}}}\:=\:-\mathrm{2}\mathit{\pi fN_{\mathrm{1}}}\:\mathit{\phi_{m} \:cos\:\omega t}}$$
其中:
$$\mathrm{\mathit{\omega \:=\:\mathrm{2}\pi f}}$$
$$\mathrm{\because -\mathit{cos\:\omega t}\:=\:\mathrm{sin}\left ( \mathit{\omega t-\mathrm{90^{\circ}}} \right )}$$
因此,
$$\mathrm{\mathit{e_{\mathrm{1}}}\:=\:\mathrm{2}\mathit{\pi fN_{\mathrm{1}}}\:\mathit{\phi_{m}\:\mathrm{sin}\left ( \mathit{\omega t-\mathrm{90^{\circ}}} \right )}}\:\cdot \cdot \cdot (2)$$
方程(2)可以寫成:
$$\mathrm{\mathit{e_{\mathrm{1}}}\:=\:\mathit{E_{m_{\mathrm{1}}}}\mathrm{sin}\left ( \mathit{\omega t-\mathrm{90^{\circ}}} \right )\:\cdot \cdot \cdot (3)}$$
其中,$\mathit{E_{m_{\mathrm{1}}}}$是感應電動勢$\mathit{e_{\mathrm{1}}}$的最大值。
$$\mathrm{\mathit{E_{\mathrm{m1}}}\:=\:\mathrm{2}\mathit{\pi fN_{\mathrm{1}}}\:\mathit{\phi_{m}}}$$
現在,對於正弦電源,原邊繞組電動勢的有效值$\mathit{E_{\mathrm{1}}}$由下式給出:
$$\mathrm{\mathit{E_{\mathrm{1}}}\:=\:\frac{\mathit{E_{m\mathrm{1}}}}{\sqrt{2}}\:=\:\frac{2\mathit{\pi fN_{\mathrm{1}}}\phi_{m}}{\sqrt{2}}}$$
$$\mathrm{\therefore\mathit{E_{\mathrm{1}}}\:=\:4.44\:\mathit{f\phi _{m}N_{\mathrm{1}}}\:\cdot \cdot \cdot (4)}$$
類似地,副邊繞組電動勢的有效值E2為:
$$\mathrm{\mathit{E_{\mathrm{2}}}\:=\:4.44\:\mathit{f\phi _{m}N_{\mathrm{2}}}\:\cdot \cdot \cdot (5)}$$
一般來說,
$$\mathrm{\mathit{E}\:=\:4.44\:\mathit{f\phi _{m}N}\:\cdot \cdot \cdot (6)}$$
方程(6)稱為變壓器的電動勢方程。
對於給定的變壓器,如果我們將電動勢方程除以電源頻率,我們得到:
$$\mathrm{\frac{\mathit{E}}{\mathit{f}}\:=\:4.44\:\phi _{m}\mathit{N}\:=\:\mathrm{Constant}}$$
這意味著每單位頻率的感應電動勢是恆定的,但在給定變壓器的原邊和副邊並不相同。
此外,從方程(4)和(5),我們有:
$$\mathrm{\frac{\mathit{E_{\mathrm{1}}}}{\mathit{E_{\mathrm{2}}}}\:=\:\frac{\mathit{N_{\mathrm{1}}}}{\mathit{N_{\mathrm{2}}}}\:or\:\frac{\mathit{E_{\mathrm{1}}}}{\mathit{N_{\mathrm{1}}}}\:=\:\frac{\mathit{E_{\mathrm{2}}}}{\mathit{N_{\mathrm{2}}}}}$$
因此,在變壓器中,原邊繞組每匝的感應電動勢等於副邊繞組每匝的感應電動勢。
數值例子
一臺單相3300/240 V,50 Hz變壓器,鐵心中的最大磁通量為0.0315 Wb。計算原邊和副邊繞組的匝數。
解答
已知資料:
$$\mathrm{\mathit{E_{\mathrm{1}}\:=\:\mathrm{3300}\:\mathrm{V}\:\mathrm{and}\:\mathit{E_{\mathrm{2}}\:=\:\mathrm{240}\:V}}}$$
$$\mathrm{\mathit{f}\:=\:50\:Hz;\:\phi _{m}\:=\:0.0315\:Wb}$$
變壓器的電動勢方程為:
$$\mathrm{\mathit{E}\:=\:4.44\:\mathit{f\phi _{m}N}}$$
因此,對於原邊繞組:
$$\mathrm{\mathit{N_{\mathrm{1}}}\:=\:\frac{\mathit{E_{\mathrm{1}}}}{4.44\:\mathit{f\phi _{m}}}\:=\:\frac{3300}{4.44\times 50\times 0.0315}}$$
$$\mathrm{\mathit{N_{\mathrm{1}}}\:=\:471.9\:=\:472}$$
同樣,對於副邊繞組:
$$\mathrm{\mathit{N_{\mathrm{2}}}\:=\:\frac{\mathit{E_{\mathrm{2}}}}{4.44\:\mathit{f\phi _{m}}}\:=\:\frac{240}{4.44\times 50\times 0.0315}}$$
$$\mathrm{\mathit{N_{\mathrm{2}}}\:=\:34.32\:=\:35}$$
繞組不可能有部分匝數。因此,匝數必須是整數。
變壓比和電壓變換比
如前章所述,變壓器的電動勢方程為:
$$\mathrm{\mathit{E}\:=\:4.44\:\mathit{f\phi _{m}\:N}}$$
對於原邊繞組:
$$\mathrm{\mathit{E_{\mathrm{1}}}\:=\:4.44\:\mathit{f\phi _{m}\:N_{\mathrm{1}}}\:\cdot \cdot \cdot (1)}$$
對於副邊繞組:
$$\mathrm{\mathit{E_{\mathrm{2}}}\:=\:4.44\:\mathit{f\phi _{m}\:N_{\mathrm{2}}}\:\cdot \cdot \cdot (2)}$$
變壓器的變壓比
從方程(1)和(2),我們有:
$$\mathrm{\frac{\mathit{E_{\mathrm{1}}}}{\mathit{E_{\mathrm{2}}}}\:=\:\frac{\mathit{N_{\mathrm{1}}}}{\mathit{N_{\mathrm{2}}}}\:=\mathrm{a}\:\:\cdot \cdot \cdot (3)}$$
常數“a”稱為變壓器的變壓比。它可以定義如下:
變壓器原邊繞組匝數與副邊繞組匝數的比值稱為變壓比。
變壓器的電壓變比
變壓器的輸出電壓與輸入電壓的比值稱為電壓變比,即:
$$\mathrm{\mathrm{變壓比}\:=\:\frac{輸出電壓}{輸入電壓}}$$
因此,如果V1是變壓器的輸入電壓,V2是輸出電壓,則其變壓比由下式給出:
$$\mathrm{\mathrm{變壓比}\:=\:\frac{\mathit{V_{\mathrm{2}}}}{\mathit{V_{\mathrm{1}}}}\:\cdot \cdot \cdot (4)}$$
對於理想變壓器,V1 = E1 和 V2 = E2,則
$$\mathrm{\mathrm{變壓比}\:=\:\frac{\mathit{V_{\mathrm{2}}}}{\mathit{V_{\mathrm{1}}}}\:=\:\frac{\mathit{E_{\mathrm{2}}}}{\mathit{E_{\mathrm{1}}}}\:=\:\:\frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}}\:=\:\frac{1}{a}\cdot \cdot \cdot (5)}$$
然而,在實際變壓器中,由於繞組電阻的存在,V1和E1之間以及V2和E2之間存在微小差異。儘管這種差異非常小,但在分析目的中,我們取V1 = E1和V2 = E2。
數值例子(1)
一個變壓器,原邊匝數為1000匝,副邊匝數為400匝,由220 V交流電源供電。計算副邊電壓和每匝電壓。
解答
已知資料:
$$\mathrm{\mathit{N_{\mathrm{1}}}\:=\:1000\:\mathrm{and}\:\mathit{N_{\mathrm{2}}}\:=\:400}$$
$$\mathrm{\mathit{V_{\mathrm{1}}}\:=\:220\:V}$$
變壓器的變壓比為:
$$\mathrm{\frac{\mathit{V_{\mathrm{1}}}}{\mathit{V_{\mathrm{2}}}}\:=\:\frac{\mathit{N_{\mathrm{1}}}}{\mathit{N_{\mathrm{2}}}}}$$
$$\mathrm{\Rightarrow \mathit{V_{\mathrm{2}}}\:=\:\mathit{V_{\mathrm{1}}}\times \frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}}\:=\:220\times \frac{400}{1000}}$$
$$\mathrm{\therefore\mathit{V_{\mathrm{2}}}\:=\:88\:\mathrm{Volts}}$$
每匝電壓由下式給出:
$$\mathrm{\mathrm{原邊繞組}\:=\:\frac{\mathit{V_{\mathrm{1}}}}{\mathit{N_{\mathrm{1}}}}\:=\:\frac{200}{1000}\:=\:0.22\:\mathrm{Volts}}$$
$$\mathrm{\mathrm{副邊繞組}\:=\:\frac{\mathit{V_{\mathrm{2}}}}{\mathit{N_{\mathrm{2}}}}\:=\:\frac{88}{400}\:=\:0.22\:\mathrm{Volts}}$$
因此,從這個例子可以看出,變壓器的每匝電壓在原邊和副邊繞組上保持相同。
數值例子(2)
一個輸出電壓為2200 V的變壓器,由220 V電源供電。如果副邊繞組有2000匝,則計算原邊繞組的匝數。
解答
已知資料:
$$\mathrm{\mathit{V_{\mathrm{1}}}\:=\:200\:\mathit{V}\:\mathrm{and}\:\mathit{V_{\mathrm{2}}}\:=\:2200\:\mathit{V}}$$
$$\mathrm{\mathit{N_{\mathrm{2}}}\:=\:2000\:\mathrm{turns}}$$
變壓器的變壓比為:
$$\mathrm{\frac{\mathit{V_{\mathrm{1}}}}{\mathit{V_{\mathrm{2}}}}\:=\:\frac{\mathit{N_{\mathrm{1}}}}{\mathit{N_{\mathrm{2}}}}}$$
$$\mathrm{\Rightarrow {\mathit{N_{\mathrm{1}}}}\:=\:\mathit{N_{\mathrm{2}}}\:\times \:\frac{\mathit{V_{\mathrm{1}}}}{\mathit{V_{\mathrm{2}}}}\:=\:\mathrm{2000}\:\times \:\frac{220}{2200}\:=\:\mathrm{200\:turns}}$$
理想變壓器和實際變壓器
理想變壓器
理想變壓器是變壓器的理想模型,具有以下特性:
原邊和副邊繞組的電阻可以忽略不計(或為零)。
沒有漏磁通,即所有磁通都流經變壓器的鐵心。
鐵心的磁導率無限大,這意味著建立鐵心磁通所需的磁動勢可以忽略不計。
沒有由於繞組電阻、磁滯和渦流引起的損耗。因此,其效率為100%。
理想變壓器的執行
我們可以分析理想變壓器在空載或負載下的執行情況,這將在以下部分討論。
理想變壓器空載執行
考慮一個空載執行的理想變壓器,即其副邊繞組是開路的,如圖1所示。原邊繞組是一個純電感線圈。
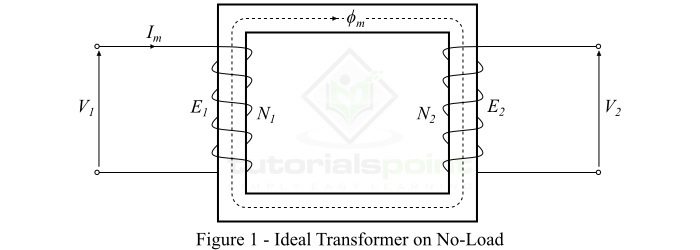
當將交流電壓$\mathit{V_{\mathrm{1}}}$施加到原邊繞組時,它會吸收很小的勵磁電流$\mathit{I_{\mathit{m}}}$以在鐵心中建立磁通,該電流滯後於施加電壓90°。勵磁電流Im在鐵心中產生與之成比例且同相位的交變磁通量$\mathit{\phi_{m}}$。這個交變磁通量($\mathit{\phi_{m}}$)透過磁耦合方式與原邊和副邊繞組連線,並在原邊繞組中感應出電動勢$\mathit{E_{\mathrm{1}}}$,並在副邊繞組中感應出電動勢$\mathit{E_{\mathrm{2}}}$。
原邊繞組感應電動勢 $\mathit{E_{\mathrm{1}}}$ 等於並與外加電壓 $\mathit{V_{\mathrm{1}}}$ 反向(根據 *楞次定律*)。電動勢 $\mathit{E_{\mathrm{1}}}$ 和 $\mathit{E_{\mathrm{2}}}$ 滯後於磁通 ($\mathit{\phi_{m}}$) 90°,但是它們的幅值取決於原邊和副邊繞組的匝數。此外,電動勢 $\mathit{E_{\mathrm{1}}}$ 和 $\mathit{E_{\mathrm{2}}}$ 彼此同相,而 $\mathit{E_{\mathrm{1}}}$ 與 $\mathit{V_{\mathrm{1}}}$ 相等且相位差 180°。
理想變壓器帶負載執行
當負載連線到理想變壓器副邊繞組的端子時,則稱變壓器帶負載執行,負載電流流過副邊繞組和負載。
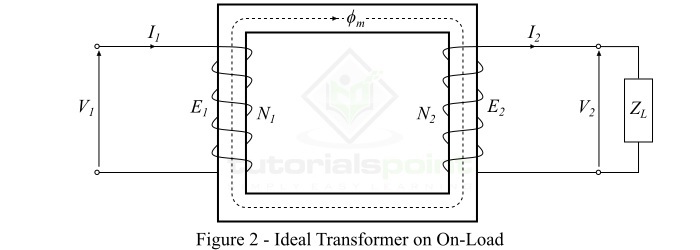
考慮一個阻抗連線在理想變壓器副邊繞組上的感性負載,如圖 2 所示。則副邊繞組電動勢 $\mathit{E_{\mathrm{2}}}$ 將導致電流 $\mathit{I_{\mathrm{2}}}$ 流過副邊繞組和負載,其計算公式為:
$$\mathrm{\mathit{I_{\mathrm{2}}}\:=\:\frac{\mathit{E_{\mathrm{2}}}}{\mathit{Z_{\mathit{L}}}}\:=\:\frac{\mathit{V_{\mathrm{2}}}}{\mathit{Z_{\mathit{L}}}}}$$
其中,對於理想變壓器,副邊繞組電動勢 $\mathit{E_{\mathrm{2}}}$ 等於副邊繞組端電壓 $\mathit{V_{\mathrm{2}}}$。
由於我們考慮的是感性負載,因此電流 $\mathit{I_{\mathrm{2}}}$ 將滯後於 $\mathit{E_{\mathrm{2}}}$ 或 $\mathit{V_{\mathrm{2}}}$ 一個 $\mathit{\phi_{\mathrm{2}}}$ 角。此外,空載電流 $\mathit{I_{\mathrm{0}}}$ 被忽略,因為變壓器是理想的。
流過副邊繞組的電流 ($\mathit{I_{\mathrm{2}}}$) 建立一個磁動勢 ($\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}$),該磁動勢產生一個與主磁通 ($\mathit{\phi_{\mathit{m}}}$) 反向的磁通 $\mathit{\phi_{\mathrm{2}}}$。結果,鐵芯中的總磁通量與其原始值發生變化,但是,鐵芯中的磁通量不應偏離其原始值。因此,為了保持鐵芯中的磁通量為其原始值,原邊電流必須產生一個磁動勢,以抵消副邊磁動勢 $\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}$ 的退磁作用。
因此,原邊電流 $\mathit{I_{\mathrm{1}}}$ 必須流動,以便
$$\mathrm{\mathit{I_{\mathrm{1}}}\mathit{N_{\mathrm{1}}}\:=\:\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}}$$
因此,原邊繞組必須汲取足夠的電流來中和副邊電流的退磁作用,以使鐵芯中的主磁通保持恆定。因此,當副邊電流 ($\mathit{I_{\mathrm{2}}}$) 增加時,原邊電流 ($\mathit{I_{\mathrm{1}}}$) 也以相同的方式增加,並保持互磁通 ($\mathit{\phi_{\mathit{m}}}$) 恆定。
在帶負載的理想變壓器中,副邊電流 $\mathit{I_{\mathrm{2}}}$ 滯後於副邊端電壓 $\mathit{V_{\mathrm{2}}}$ 一個 $\mathit{\phi _{\mathrm{2}}}$ 角。
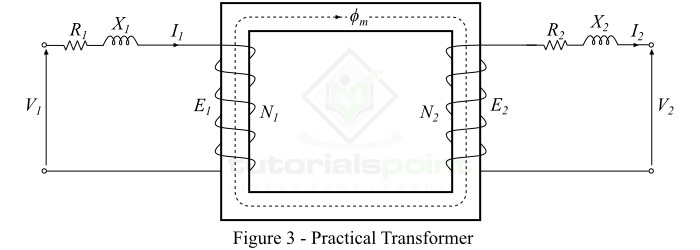
實際變壓器
實際變壓器具有以下特性:
原邊和副邊繞組具有有限的電阻。
存在漏磁通,即並非所有磁通都限制在磁芯內。
磁芯具有有限的磁導率,因此需要相當大的磁動勢來在鐵芯中建立磁通。
由於繞組電阻、磁滯和渦流,變壓器會產生損耗。因此,實際變壓器的效率總是小於 100%。
典型的實際變壓器的分析模型如圖 3 所示。
實際變壓器的特性
以下是實際變壓器的重要特性:
繞組電阻
變壓器的繞組通常由銅導體組成。因此,原邊和副邊繞組都將具有繞組電阻,這會在變壓器中產生銅損或 $\mathit{i^{\mathrm{2}} \mathit{R}}$ 損耗。原邊繞組電阻 $\mathit{R_{\mathrm{1}}}$ 和副邊繞組電阻 $\mathit{R_{\mathrm{2}}}$ 分別與各自的繞組串聯,如圖 3 所示。
鐵損或鐵芯損耗
變壓器的鐵芯經受交變磁通,因此鐵芯中會產生渦流損耗和磁滯損耗。磁滯損耗和渦流損耗合稱為 **鐵損** 或 **鐵芯損耗**。變壓器的鐵損取決於電源頻率、鐵芯中的最大磁通密度、鐵芯體積和疊片厚度等。在實際變壓器中,鐵損的幅值實際上是恆定的且很小。
漏磁通
流過原邊繞組的電流產生磁通。連線原邊和副邊繞組的磁通 $\mathit{\phi _{\mathit{m}}}$ 是有用磁通,稱為 **互磁通**。但是,原邊電流產生的部分磁通 ($\mathit{\phi _{\mathrm{1}}}$) 不與副邊繞組相連。
當負載連線到副邊繞組時,電流流過它併產生磁通 ($\mathit{\phi _{\mathrm{2}}}$),該磁通僅與副邊繞組相連。因此,僅與其各自繞組相連的 $\mathit{\phi _{\mathrm{1}}}$ 的一部分和磁通 $\mathit{\phi _{\mathrm{2}}}$ 稱為 **漏磁通**。
漏磁通的路徑透過空氣,空氣具有非常高的磁阻。因此,原邊漏磁通 ($\mathit{\phi _{\mathrm{1}}}$) 的作用是在原邊繞組中引入一個與之串聯的電抗 ($ \mathit{X_{\mathrm{1}}}$)。類似地,副邊漏磁通 ($\mathit{\phi _{\mathrm{2}}}$) 在副邊繞組中引入一個與之串聯的電抗 ($ \mathit{X_{\mathrm{2}}}$),如圖 3 所示。
然而,實際變壓器中的漏磁通非常小(約為 $\mathit{\phi _{m}}$ 的 5%),但不能忽略。因為漏磁通的路徑是空氣,空氣具有非常高的磁阻。因此,它需要相當大的磁動勢。
鐵芯材料的有限磁導率
一般來說,實際變壓器的鐵芯由高階矽鋼製成,它具有特定的相對磁導率 ($\mathit{\mu _{r}}$)。因此,鐵芯在一定的磁通密度值下會飽和。因此,實際變壓器的鐵芯具有有限的磁導率,因此在磁通路徑中具有磁阻。
直流變壓器
在緒論中,我們將電力變壓器定義為交流電機,因為它僅在交流電下工作。因此,變壓器不能改變(增加或減少)直流電壓的值。在本章中,我們將瞭解為什麼變壓器不適用於直流電的原因。
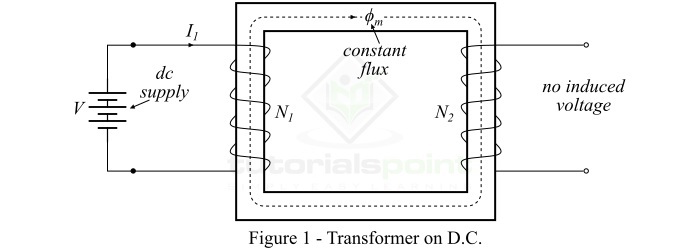
考慮一個如圖 1 所示的電力變壓器,它連線到電池(或直流電壓源)V。當我們將此直流電壓 V 加到變壓器的原邊繞組時,它將吸收恆定電流(直流電),因此會產生恆定的磁通量流過磁芯。
根據電磁感應原理,只有當線圈或導體經受變化的磁場時,才能線上圈或導體中感應電動勢,即:
$$\mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}}$$
因此,加到原邊繞組上的直流電壓不會在原邊繞組或副邊繞組中感應電動勢。因此,此討論證明了 *變壓器不適用於直流電源。事實上,將直流電源連線到變壓器的原邊繞組可能是危險的*。
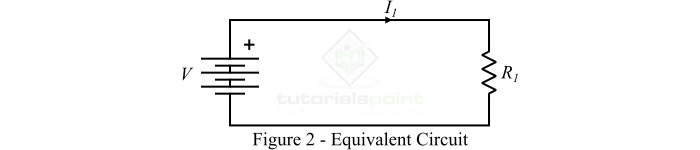
連線到直流電壓的變壓器的等效原邊繞組電路如圖 2 所示。在這種情況下,原邊繞組中沒有自感電動勢來阻止外加電壓 *V(根據楞次定律)*,原邊繞組中的電流由下式給出:
$$\mathrm{\mathit{I_{\mathrm{1}}}\:=\:\frac{\mathit{V}}{\mathit{R_{\mathrm{1}}}}}$$
其中,$\mathit{R_{\mathrm{1}}}$ 是原邊繞組的電阻。由於 $\mathit{R_{1}}$ 的值很小,因此流過原邊繞組的電流 $\mathit{I_{\mathrm{1}}}$ 將非常大。這種大電流會導致變壓器過熱和燒燬,或者保險絲會熔斷。因此,*我們絕不能將變壓器的原邊繞組連線到直流電源,因為它可能會損壞變壓器或造成觸電事故*。
變壓器的損耗
實際變壓器中可能發生以下功率損耗:
鐵損或鐵芯損耗
銅損或 $\mathit{I^{2}R}$ 損耗
雜散損耗
介質損耗
在變壓器中,這些功率損耗以熱量的形式出現,並導致兩個主要問題:
增加變壓器的溫度。
降低變壓器的效率。
鐵損或鐵芯損耗
**鐵損** 是由於交變磁通流過變壓器的磁芯而產生的。由於這個原因,鐵損也稱為 **鐵芯損耗**。我們通常用符號 ($\mathit{P_{i}}$) 表示鐵損。鐵損包括磁滯損耗 ($\mathit{P_{h}}$) 和渦流損耗 ($\mathit{P_{e}}$)。因此,鐵損由磁滯損耗和渦流損耗之和給出,即
$$\mathrm{\mathrm{鐵損,}\mathit{P_{i}}\:=\:\mathrm{磁滯損耗(\mathit{P_{h}})}\:+\:\mathrm{渦流損耗(\mathit{P_{e}})}}$$
透過對變壓器進行 **開路試驗** 來確定磁滯損耗和渦流損耗(或鐵損)。
磁滯損耗和渦流損耗的經驗公式為:
$$\mathrm{\mathit{P_{h}}\:=\:\mathit{k_{h}f\:B_{m}^{x}}\:\cdot \cdot \cdot (1)}$$
$$\mathrm{\mathit{P_{e}}\:=\:\mathit{ke\:B_{m}^{\mathrm{2}}\:f^{\mathrm{2}}t^{\mathrm{2}}}\:\cdot \cdot \cdot (2)}$$
其中:
$\mathit{B_{m}}$ 的指數,即“$\mathit{x}$”稱為 **Steinmetz 常數**。根據鐵芯材料的特性,其值在 1.5 到 2.5 之間。
**$\mathit{k_{h}}$** 是一個比例常數,其值取決於鐵芯材料的體積和質量。
**$\mathit{k_{e}}$** 是一個比例常數,取決於鐵芯材料的體積和電阻率。
**$\mathit{f}$** 是鐵芯中交變磁通的頻率。
**$\mathit{B_{m}}$** 是鐵芯中的最大磁通密度。
**$\mathit{t}$** 是每個鐵芯疊片的厚度。
因此,總鐵損或鐵芯損耗也可以寫成:
$$\mathrm{\mathit{P_{i}}\:=\:\mathit{k_{h}f\:B_{m}^{x}}\:+\:\mathit{ke\:B_{m}^{\mathrm{2}}\:f^{\mathrm{2}}t^{\mathrm{2}}}\:\cdot \cdot \cdot (3)}$$
由於變壓器的輸入電壓近似等於原邊繞組中的感應電壓,即
$$\mathrm{\mathit{V_{\mathrm{1}}}\:=\:\mathit{E_{\mathrm{1}}}\:=\:4.44\:\mathit{f\phi _{m}N_{\mathrm{1}}}}$$
$$\mathrm{\Rightarrow \mathit{V_{\mathrm{1}}}\:=\:4.44\:\mathit{f\:B_{m}AN_{\mathrm{1}}}}$$
其中,$\mathit{A}$ 是變壓器鐵芯的橫截面積,$\mathit{N_{1}}$ 是原邊繞組的匝數,$\mathit{f}$ 是電源頻率。
$$\mathrm{\therefore \mathit{B_{m}}\:=\:\frac{\mathit{V_{\mathrm{1}}}}{4.44\mathit{fAN_{\mathrm{1}}}}\:\cdot \cdot \cdot (4)}$$
因此,根據公式 (1) 和 (4),我們得到:
$$\mathrm{\mathit{P_{h}}\:=\:\mathit{k_{h}f}\left ( \frac{\mathit{V_{\mathrm{1}}}}{4.44\mathit{fAN_{\mathrm{1}}}} \right )^{x}}$$
$$\mathrm{\Rightarrow \mathit{P_{h}}\:=\:\mathit{k_{h}f}\left ( \frac{\mathrm{1}}{4.44\mathit{AN_{\mathrm{1}}}} \right )^{x}\cdot \left ( \frac{\mathit{V_{\mathrm{1}}}}{\mathit{f}} \right )^{x}}$$
$$ \mathrm{\Rightarrow \mathit{P_{h}}\:=\:\mathit{k_{h}}\left ( \frac{\mathrm{1}}{4.44\mathit{AN_{\mathrm{1}}}} \right )^{x}\cdot \mathit{V_{\mathrm{1}}^{x}}\:\mathit{f^{(\mathrm{1}-x)}}\:\cdot \cdot \cdot (5)} $$
因此,公式 (5) 表明 *磁滯損耗取決於輸入電壓和電源頻率*。
同樣,由公式 (2) 和 (4),我們得到:
$$ \mathrm{\mathit{P_{e}}\:=\:\mathit{k_{e}f^{\mathrm{2}}t^{\mathrm{2}}}\left ( \frac{\mathit{V_{\mathrm{1}}}}{4.44\mathit{fAN_{\mathrm{1}}}} \right )^{\mathrm{2}}} $$
$$ \mathrm{\Rightarrow \mathit{P_{e}}\:=\:\mathit{k_{e}\left ( \frac{\mathit{V_{\mathrm{1}}}}{\mathrm{4.44}\mathit{AN_{\mathrm{1}}}} \right )^{\mathrm{2}}\mathit{t^{\mathrm{2}}}\:\cdot \cdot \cdot \mathrm{(6)}}} $$
因此,從公式 (6) 可以得出結論:*變壓器中的渦流損耗與輸入電壓的平方成正比,並且與電源頻率無關*。
因此,總鐵損也可以寫成:
$$ \mathrm{\mathit{P_{i}}\:=\:\mathit{k_{h}\left ( \frac{\mathrm{1}}{\mathrm{4.44}\mathit{AN_{\mathrm{1}}}} \right )^{\mathrm{2}}\cdot \mathit{V_{\mathrm{1}}^{\mathit{x}}f^{(\mathrm{1-x})}}\:+\:\mathit{k_{e}}\left ( \frac{V_{\mathrm{1}}}{\mathrm{4.44}\mathit{AN_{\mathrm{1}}}} \right )^{\mathrm{2}}\mathit{t^{\mathrm{2}}}\:\cdot \cdot \cdot \left ( \mathrm{7} \right )}} $$
在實際應用中,變壓器連線到恆定頻率和恆定電壓的電源,因此,*f* 和 *Bm* 均為常數。因此,鐵損在所有負載下實際上保持不變。
我們可以透過使用高矽含量鋼材來構成變壓器鐵芯來減少磁滯損耗,同時可以透過使用薄層疊鐵芯代替實心鐵芯來最大限度地減少渦流損耗。對變壓器進行 **空載試驗** 以確定鐵損。
銅損或 $\mathit{I^{2}R}$ 損耗
變壓器中由於初級和次級繞組的歐姆電阻而產生的功率損耗稱為 **銅損或 I²R 損耗**。我們通常用 Pc 表示銅損。因此,變壓器的總銅損是初級繞組功率損耗和次級繞組功率損耗之和,即:
$$ \mathrm{\mathit{P_{c}}\:=\:\mathrm{初級繞組銅損\:+\:次級繞組銅損}} $$
$$ \mathrm{\Rightarrow \mathit{P_{c}}\:=\:\mathit{I_{\mathrm{1}}^{\mathrm{2}}}\mathit{R_{\mathrm{1}}}\:+\:\mathit{I_{\mathrm{2}}^{\mathrm{2}}}\mathit{R_{\mathrm{2}}}\:\cdot \cdot \cdot (8)} $$
因為:
$$\mathrm{\mathit{I_{\mathrm{1}}}\mathit{N_{\mathrm{1}}}\:=\:\mathit{I_{\mathrm{2}}}\mathit{N_{\mathrm{2}}}}$$
$$ \mathrm{\Rightarrow \mathit{I_{\mathrm{1}}}\:=\:\left ( \frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}} \right )\mathit{I_{\mathrm{2}}}\:\cdot \cdot \cdot (9)} $$
$$ \mathrm{\therefore \mathit{P_{c}}\:=\:\left [ \left ( \frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}} \right )I_{\mathrm{2}} \right ]^{\mathrm{2}}\:\mathit{R_{\mathrm{1}}}\:+\:\mathit{I_{\mathrm{2}}^{\mathrm{2}}}\mathit{R_{\mathrm{2}}}\:=\:\left [ \left ( \frac{\mathit{N_{\mathrm{2}}}}{\mathit{N_{\mathrm{1}}}} \right )^{\mathrm{2}}\mathit{R_{\mathrm{1}}}\:+\:\mathit{R_{\mathrm{2}}} \right ]\mathit{I_{\mathrm{2}}^{\mathrm{2}}}\:\cdot \cdot \cdot (10)} $$
從公式 (10) 可以清楚地看出,*變壓器的銅損隨負載電流的平方而變化*。因此,銅損也稱為“可變損耗”,因為在實際應用中,變壓器承受可變負載,因此具有可變負載電流。
我們對變壓器進行“短路試驗”以確定其銅損的值。在實際變壓器中,銅損約佔變壓器總功率損耗的 90%。
雜散損耗
在實際變壓器中,一部分總磁通沿空氣路徑傳播,這部分磁通稱為 **漏磁通**。該漏磁通會在導電或金屬部件(如變壓器油箱)中產生渦流。這些渦流會導致功率損耗,這被稱為 **雜散損耗**。
介質損耗
變壓器絕緣材料(如油、固體絕緣等)中發生的功率損耗稱為 **介質損耗**。介質損耗僅在高壓變壓器中才顯著。
雖然在實際應用中,雜散損耗和介質損耗非常小,且為常數,可以忽略不計。
從以上討論可以看出,變壓器存在一些恆定損耗和一些可變損耗。因此,我們可以將變壓器中的損耗分為兩種型別,即 **恆定損耗** 和 **可變損耗**。
因此,變壓器的總損耗是恆定損耗和可變損耗之和,即:
Total losses in transformer = Constant losses + Variable losses
變壓器的效率
變壓器效率
變壓器的輸出功率與輸入功率之比稱為 **變壓器效率**。變壓器效率用希臘字母 Eta (η) 表示。
$$ \mathrm{效率, \eta \:=\:\frac{輸出功率}{輸入功率}} $$
根據此定義,似乎我們可以透過直接載入變壓器並測量輸入功率和輸出功率來確定變壓器的效率。但是,這種效率測定方法存在以下缺點:
在實際應用中,變壓器的效率非常高,輸入和輸出瓦特表中很小的誤差(例如 1%)可能會導致荒謬的結果。因此,這種方法可能會得出效率超過 100% 的結果。
在這種方法中,變壓器已載入,因此會浪費相當多的功率。因此,對於大型變壓器,這種方法在經濟上不可行。
很難找到能夠吸收所有輸出功率的負載。
這種方法不會提供有關變壓器損耗的任何資訊。
因此,由於這些限制,很少使用直接載入法來確定變壓器的效率。在實際應用中,我們使用空載試驗和短路試驗來確定變壓器效率。
對於實際變壓器,輸入功率由下式給出:
$$ \mathrm{輸入功率\:=\:\mathrm{輸出功率\:+\:損耗}} $$
因此,變壓器效率也可以使用以下表達式計算:
$$ \mathrm{\eta \:=\:\frac{輸出功率}{輸出功率\:+\:損耗}} $$
$$ \mathrm{\Rightarrow \eta \:=\:\frac{VA\times 功率因數}{\left ( VA\times 功率因數 \right )\:+\:損耗}} $$
其中:
$$ \mathrm{輸出功率\:=\:VA\times 功率因數} $$
並且,損耗可以透過變壓器測試來確定。
根據變壓器試驗得到的效率
當我們進行變壓器測試時,會得到以下結果:
根據空載試驗:
$$ \mathrm{額定負載鐵損\:=\:\mathit{P_{i}}} $$
根據短路試驗:
$$ \mathrm{額定負載銅損\:=\:\mathit{P_{c}}} $$
因此,變壓器滿載時的總損耗為
$$ \mathrm{總滿載損耗\:=\:\mathit{P_{i}+\:P_{c}}} $$
現在,我們能夠在任何功率因數下確定變壓器的滿載效率,而無需實際載入變壓器。
$$ \mathrm{\mathit{n_{FL}}\:=\:\frac{(VA)_{\mathit{FL}}\times 功率因數}{[(VA)_{\mathit{FL}}\times 功率因數]+\:\mathit{P_{i}}+\mathit{P_{c}}}} $$
此外,變壓器在任何等於 *x × 滿載* 的負載下的效率。其中,x 是負載的比例。在這種情況下,對應於給定負載的總損耗為:
$$ \mathrm{(總損耗)_{x}\:=\:\mathit{P_{i}+\:x^{\mathrm{2}}\mathit{P_{c}}}} $$
這是因為鐵損 (Pi) 是恆定損耗,因此在所有負載下都保持不變,而銅損與負載電流的平方成正比。
$$ \mathrm{\therefore\eta _{x}\:=\: \frac{\mathit{x}\times (VA)_{\mathit{FL}}\times 功率因數}{[\mathit{x}\times (VA)_{\mathit{FL}}\times 功率因數]+\:\mathit{P_{i}}+\:x^{\mathrm{2}}\mathit{P_{c}}}} $$
最大效率的條件
對於給定的變壓器,我們有:
$$ \mathrm{輸出功率\:=\:\mathit{V_{\mathrm{2}}I_{\mathrm{2}}cos\phi _{\mathrm{2}}}} $$
設變壓器參考次級側,則 *Ro2* 是變壓器的總電阻。總銅損由下式給出:
$$ \mathrm{\mathit{P_{c}}\:=\:\mathit{I_{\mathrm{2}}^{\mathrm{2}}\mathit{R_{o\mathrm{2}}}}} $$
因此,變壓器效率由下式給出:
$$ \mathrm{\eta \:=\:\frac{\mathit{V_{\mathrm{2}}}I_{\mathrm{2}}cos\phi _{\mathrm{2}}}{\mathit{V_{\mathrm{2}}I_{\mathrm{2}}cos\phi _{\mathrm{2}}}+\mathit{P_{i}}+\mathit{I_{\mathrm{2}}^{\mathrm{2}}}R_{o\mathrm{2}}}} $$
重新排列表達式,我們得到:
$$ \mathrm{\eta \:=\:\frac{\mathit{V_{\mathrm{2}}}cos\phi _{\mathrm{2}}}{\mathit{V_{\mathrm{2}}cos\phi _{\mathrm{2}}}+\left ( \mathit{\frac{P_{i}}{I_{\mathrm{2}}}} \right )+\mathit{I_{\mathrm{2}}}R_{o\mathrm{2}}}\:=\:\mathit{\frac{V_{\mathrm{2}}cos\phi _{\mathrm{2}}}{D}}\:\cdot \cdot \cdot (1)} $$
在實際應用中,次級電壓 *V2* 近似恆定。因此,對於給定功率因數的負載,變壓器效率取決於負載電流 (*I2*)。從公式 (1) 可以看出,分子是常數,為了使效率最大化,分母 (D) 應最小,即
$$ \mathrm{\mathit{\frac{d(D)}{dI_{\mathrm{2}}}}\:=\:0} $$
$$ \mathrm{\Rightarrow\mathit{\frac{d}{dI_{\mathrm{2}}}}\left [ \mathit{V_{\mathrm{2}}cos\phi _{\mathrm{2}}}+\left ( \mathit{\frac{P_{i}}{I_{\mathrm{2}}}}\right )+\mathit{I_{\mathrm{2}} R_{0\mathrm{2}}} \right ]\:=\:0} $$
$$ \mathrm{\Rightarrow 0-\left ( \mathit{\frac{P_{i}}{I_{\mathrm{2}}}} \right )+\mathit{R_{o\mathrm{2}}}\:=\:0} $$
$$ \mathrm{\Rightarrow \mathit{P_{i}}\:=\:\mathit{I_{\mathrm{2}}^{\mathrm{2}}R_{o\mathrm{2}}}} $$
$$ \mathrm{\Rightarrow 鐵損\:=\:銅損} $$
因此,*對於給定的功率因數,當恆定鐵損等於可變銅損時,變壓器的效率最大*。
任何負載下的最大效率由下式給出:
$$ \mathrm{\mathit{\eta _{max}}\:=\:\frac{\mathit{x\times (VA)_{\mathit{FL}}\times 功率因數}}{[\mathit{x\times (VA)_{\mathit{FL}}}\times 功率因數]+\:2\mathit{P_{i}}}} $$
此外,對應於變壓器最大效率的負載電流 (*I2*) 為:
$$ \mathrm{\mathit{I_{\mathrm{2}}}\:=\:\sqrt{\frac{\mathit{P_{i}}}{R_{o2}}}} $$
數值例子
在一個 100 kVA 的變壓器中,鐵損為 450 W,滿載銅損為 900 W。求該變壓器在滿載時的效率和最大效率,其中負載功率因數為 0.8 滯後。
解答
已知資料:
滿載 VA = 100 kVA = 100 × 1000 VA
鐵損,Pi = 450 W
銅損,Pc = 900 W
cosφ2 = 0.8
變壓器滿載效率:
$$ \mathrm{總損耗\:=\:450\:+\:900\:=\:1350\:W} $$
$$ \mathrm{\mathit{\eta _{\mathit{FL}}}\:=\:\frac{(VA)_{\mathit{FL}}\times 功率因數}{[(VA)_{\mathit{FL}}\times 功率因數]+\:總損耗}} $$
$$ \mathrm{\Rightarrow \mathit{\eta _{\mathit{FL}}}\:=\:\frac{100\times 1000\times 0.8}{(100\times 1000\times 0.8)+1350}\:=\:\frac{80000}{81350}\:=\:0.9834} $$
$$ \mathrm{\therefore \eta _{\mathit{FL}}\:=\:0.9834\times 100\%\:=\:98.34\%} $$
變壓器的最大效率:
對於最大效率:
$$ \mathrm{鐵損\:=\:銅損} $$
$$ \mathrm{\therefore \eta _{\mathit{max}}\:=\:\frac{(VA)_{\mathit{FL}}\times 功率因數}{[(VA)_{\mathit{FL}}\times 功率因數]+2\mathit{P_{i}}}} $$
$$ \mathrm{\Rightarrow \eta _{\mathit{max}}\:=\:\frac{100\times 1000\times 0.8}{(100\times 1000\times 0.8)+(2\times 450)}\:=\:0.9888} $$
$$ \mathrm{\therefore \eta _{\mathit{max}}\:=\:0.9888\times 100\%\:=\:98.88\%} $$
三相變壓器
在實際應用中,電力是透過三相系統發電、傳輸和分配的。因此,我們需要 **三相變壓器** 來在電力系統網路的各個階段升壓或降壓。
我們可以透過以下兩種方式之一來構造三相變壓器:
我們可以連線三個獨立的單相變壓器來進行三相執行。這種佈置被稱為 **三相變壓器組**。
我們可以構造一個單一的具有磁芯和所有三個相繞組的三相變壓器。整個元件組合在一個單一結構中。
三相變壓器的繞組可以按以下方式連線:
**星形-星形連線** - 在這種情況下,初級和次級繞組都採用星形連線。
**三角形-三角形連線** - 在這種情況下,初級和次級繞組都採用三角形連線。
Δ-Y 接法 − 此接法中,原邊繞組採用三角形連線,副邊繞組採用星形連線。
Y-Δ 接法 − 此接法中,原邊繞組採用星形連線,副邊繞組採用三角形連線。
三相變壓器的結構
三相變壓器可以透過兩種方式構造,即核心式結構和殼式結構。
核心式結構
在三相變壓器的核心式結構中,磁芯具有三個垂直鐵心柱和兩個水平橫截面,如圖 1 所示。此處,每一鐵心柱上都放置一對原邊和副邊繞組。低壓 (lv) 繞組放置在磁芯旁邊,高壓 (hv) 繞組繞在 lv 繞組周圍。
殼式結構
殼式三相變壓器可以透過將三個單相殼式變壓器堆疊在一起構成,如圖 2 所示。在這種情況下,原邊和副邊繞組都放置在中心鐵心柱上,兩個外側鐵心柱作為磁通路徑。殼式三相變壓器的行為與三臺單相變壓器組幾乎相同。
三臺單相變壓器組的優點
與三相單元變壓器相比,三臺單相變壓器組的主要優點如下:
當變壓器組中的一臺單相變壓器損壞並與系統隔離時,剩餘的兩臺變壓器可在開三角形連線中供電。
在變壓器組中,可以提供 kVA 額定值高於其他變壓器的單相變壓器以供應不平衡負載。
對於三臺單相變壓器組,備用要求較低。
運輸單相變壓器比運輸三相變壓器更方便。
三相單元變壓器的優點
對於相同的 kVA 額定值,三相單元變壓器與三臺單相變壓器組相比具有以下優點:
三相單元變壓器體積更小,重量更輕,成本更低。
它比變壓器組效率更高。
安裝簡單。
根據需要,我們同時使用變壓器組和三相單元變壓器。但是,通常的做法是使用三相單元變壓器。
變壓器的型別
根據原邊和副邊繞組的匝數,變壓器可以分為以下三種類型:
升壓變壓器
降壓變壓器
一比一變壓器
根據應用,我們可以將變壓器分為以下三種主要型別:
電力變壓器
配電變壓器
儀用變壓器
升壓變壓器
副邊繞組匝數大於原邊繞組匝數的變壓器,其輸出電壓大於輸入電壓,稱為升壓變壓器。在電力系統中,升壓變壓器用於將低電壓升高到更高的值以進行傳輸。
降壓變壓器
副邊繞組匝數小於原邊繞組匝數的變壓器,其輸出電壓小於輸入電壓,稱為降壓變壓器。在電力系統中,降壓變壓器用於將高電壓降低到較低的電壓值,用於配電和利用。
一比一 (1:1) 變壓器
原邊繞組和副邊繞組匝數相同的變壓器,其輸出電壓等於輸入電壓,稱為一比一變壓器。也稱為隔離變壓器。它應用於需要將兩個電路電隔離但磁耦合以進行能量傳輸的領域。
電力變壓器
伏安 (VA) 額定值較高的變壓器,通常為兆伏安或吉伏安級,稱為電力變壓器。電力變壓器設計為以幾乎恆定的負載執行,該負載等於其額定值。這些變壓器用於發電站、接收站和電力傳輸線路末端的變電站,用於升壓或降壓。
實際上,電力變壓器在負荷期間投入執行,而在輕負荷期間斷開連線。這些變壓器設計為在滿載或接近滿載時具有最大效率。但是,電力變壓器的設計具有相當高的漏抗。因此,對於電力變壓器,高漏抗的限流作用比電壓調整更重要。
配電變壓器
用於將高電壓降低到低電壓以進行配電的變壓器稱為配電變壓器。配電變壓器設計為以可變負載執行,該負載遠小於其額定值。因此,這些變壓器設計為在負載為滿載的 ½ 到 ¾ 之間時具有最大效率。配電變壓器全天候執行,無論是否承載任何負載。
儀用變壓器
很難用簡單的測量裝置測量高交流電流和電壓。因此,為了簡化高交流電流和電壓的測量,我們使用專門設計的變壓器,稱為儀用變壓器。透過使用儀用變壓器,我們可以用低量程交流測量裝置測量高交流量。
根據變換量的型別,儀用變壓器分為以下兩種型別:
電流互感器 (C.T.)
電壓互感器 (P.T.)
電流互感器
電流互感器是一種儀用變壓器,用於將電力線路的高交流電流降低到可測量的低值。基本上,電流互感器是一種升壓降流變壓器。它有一個幾匝粗導線的原邊繞組和一個多匝細導線的副邊繞組。電流互感器的原邊繞組與需要測量電流的線路串聯連線,副邊繞組與低量程交流電流表連線以測量和指示電流。
電壓互感器
電壓互感器是一種降壓變壓器,用於將高線路電壓降低到可測量的值。電壓互感器的原邊繞組匝數很多,而副邊繞組匝數很少。原邊繞組連線到需要測量電壓的電力線路,副邊繞組連線到低量程交流電壓表以指示測得的電壓值。
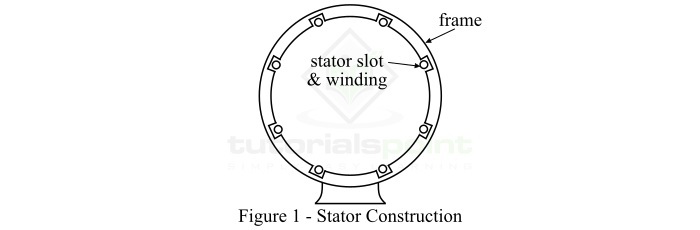
直流電機的構造
能夠將直流電 (dc) 能量轉換為機械能或將機械能轉換為直流電 (dc) 能量的機電裝置稱為直流電機。
如果直流電機將直流電能轉換為機械能,則稱為直流電動機。如果電機將機械能轉換為直流電能,則稱為直流發電機。直流電動機和直流發電機的結構相似。
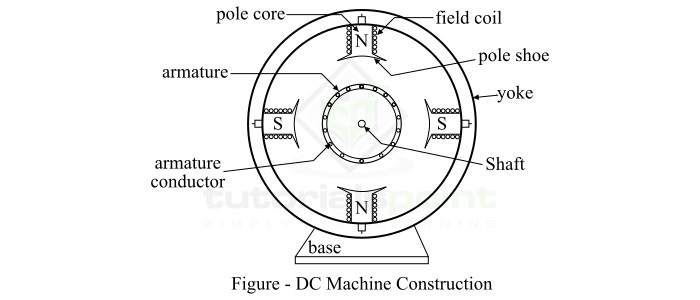
典型的直流電機包含以下主要部件:
機座或機架
電樞
勵磁系統
換向器
電刷
軸承
直流電機的示意圖如下所示:
現在讓我們更詳細地討論每個元件。
機座或機架
機座是直流電機的外部框架。它由具有高磁導率和高機械強度的材料製成。實際上,直流電機的機座由鑄鋼製成。
直流電機的機座或機架具有以下主要用途:
它保護內部機器部件(如電樞、繞組、磁極等)免受機械損壞。
機座容納磁場系統。
它為工作磁通提供低磁阻路徑。
它透過軸承支撐轉子或電樞。
電樞
在直流電機(電動機或發電機)中,電樞是可以在支撐軸承上自由旋轉的導體或線圈系統。工作轉矩和電動勢在電樞線圈中產生。電樞由兩個主要部分組成,即電樞鐵芯和電樞繞組。
電樞鐵芯是一個實心圓柱形結構,由高磁導率的薄矽鋼片製成。在鐵芯的外圓周上切割槽以承載電樞繞組。
電樞繞組由銅線製成。直流電機的電樞繞組通常是模製繞組。根據電樞導體的端部連線方式,電樞繞組可以分為兩種型別,即疊繞組和波繞組。繞組型別決定了電機的電壓和電流額定值。對於疊繞組,電流流動的並聯支路數 (A) 等於電機中的磁極數 (P)。另一方面,對於波繞組,並聯支路數 (A) 等於 2。
勵磁系統
勵磁系統是直流電機的一部分,它在電機中產生工作磁通。它基本上是一個由直流電源勵磁的電磁體系統。在直流電機中,勵磁系統是電機的靜止部分,它固定在電機的機座或機架上。直流電機勵磁系統主要有三部分:磁極鐵芯、磁極靴和勵磁繞組。
磁極鐵芯由薄鋼片製成。磁極鐵芯的一端固定在機架上,另一端有磁極靴。磁極鐵芯承載勵磁繞組。
磁極靴是磁極鐵芯的突出部分,具有較大的橫截面積。磁極靴有助於在氣隙中均勻地分佈磁通,併為磁通提供低磁阻路徑。它也支撐勵磁繞組。
勵磁繞組由銅線製成。勵磁繞組是模製繞組,並繞在磁極鐵芯周圍。當勵磁繞組由直流電源勵磁時,它們會變成電磁體並在電機中產生磁通。
換向器
換向器是直流電機的重要部件之一。它基本上是機械整流器。它是一個圓柱形裝置,由銅製成。換向器的外圓周有 V 形槽,用於承載換向片。換向片是插入槽中的銅條。這些片段由雲母彼此絕緣。換向器安裝在直流電機軸上,位於電樞的一側。電樞導體藉助銅耳連線到換向片。
換向器執行以下兩個主要功能:
在直流發電機中,它從電樞導體收集電流。在直流電動機中,它向電樞導體供電。
藉助電刷,它將電樞的交流電轉換為外部電路中的單向電流,反之亦然。
電刷
電刷用於與旋轉的換向器進行電氣連線。它們從(或向)運動的換向器收集(或供應)電流。電刷通常由碳製成。它們裝在電刷架中,並藉助彈簧壓力與換向器表面接觸。
軸承
直流電機中使用軸承來減少摩擦損失。因此,直流電機中軸承的主要功能是以最小的摩擦支撐電機軸。在直流電機中,通常使用滾珠軸承或滾柱軸承。
直流電機的型別
直流電機是一種將直流形式的電能轉換為機械能,或將機械能轉換為直流形式的電能的裝置。因此,直流電機基本上是一種機電能量轉換裝置。
根據能量轉換,直流電機可分為以下兩種型別:
直流電動機
直流發電機
直流電動機和直流發電機的基本結構幾乎相同。然而,直流電動機和直流發電機執行中涉及的基本原理是不同的。
每個直流電機都包含一套導體系統和一套磁體或電磁體系統。導體系統稱為電樞,在直流電機中,它安裝在可移動的軸上。磁體或電磁體系統稱為勵磁系統,它產生所需的工磁通量。
直流電動機
圖1顯示了直流電動機的框圖。(此處應插入圖1)
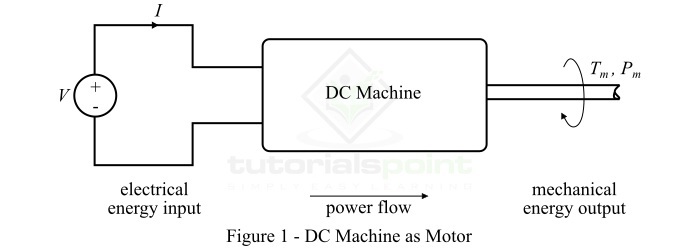
當直流電機設計用於將直流電能轉換為旋轉機械能時,它被稱為直流電動機。因此,在直流電動機的情況下,電能透過輸入端子供給電機,機械能輸出則以軸的旋轉形式從軸上獲取。
直流發電機
圖2顯示了直流發電機的框圖。(此處應插入圖2)

能夠將機械能輸入轉換為電能輸出的直流電機稱為直流發電機。因此,在直流發電機中,來自發動機、渦輪機等能源的機械能以軸的旋轉能的形式提供給直流電機,直流電能則作為輸出從電樞端子獲得。
直流發電機的原理
直流發電機的執行原理基於法拉第電磁感應定律。根據該定律,當穿過導體或線圈的磁通量發生變化時,導體或線圈中就會感應出電動勢。該感應電動勢的大小由下式給出:
$${\mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}\:\cdot \cdot \cdot (1)}}$$
其中,$\phi$是線圈的磁通鏈,N是線圈的匝數。
在直流發電機的情況下,磁通量 ($\phi$) 保持靜止,線圈旋轉。線圈旋轉而磁通靜止時感應的電動勢稱為動態感應電動勢。

為了理解直流發電機的執行原理,我們考慮一個單環直流發電機(即 *N = 1*),如圖所示。(此處應插入圖示) 此處,線圈由某個原動機(機械能的來源)旋轉,並且線圈的磁通鏈發生變化。
設 $\phi$ 為電機每個磁極產生的平均磁通量,則發電機中的平均感應電動勢由下式給出:
$${\mathrm{\mathit{E_{av}}\:=\:\frac{\mathit{d\phi }}{\mathit{dt}}\:=\:\mathrm{線圈每秒切割的磁通量}}}$$
$${\mathrm{\Rightarrow \mathit{E_{av}}\:=\:\mathrm{一次旋轉切割的磁通量\:\times \:每秒旋轉次數}}}$$
$${\mathrm{\Rightarrow \mathit{E_{av}}\:=\:\mathrm{\left ( 每極磁通量\times 極數 \right )}\:\times \:\mathrm{每秒旋轉次數}}}$$
$${\mathrm{\therefore \mathit{E_{av}}\:=\:\mathit{\phi \:\times P\:\times \:n}\:\cdot \cdot \cdot (2)}}$$
其中,*P* 是發電機的總極數,*n* 是線圈的每秒旋轉速度。公式(2)給出了單環直流發電機中的平均感應電動勢。
以下幾點解釋了直流發電機的執行原理:
位置1 - 感應電動勢為零,因為線圈邊的運動與磁通量平行。
位置2 - 線圈邊與磁通量成一定角度運動,因此在環路中產生較小的電動勢。
位置3 - 線圈邊與磁通量成直角運動,因此感應電動勢最大。
位置4 - 線圈邊以一定角度切割磁通量,因此線上圈邊中感應出較小的電動勢。
位置5 - 線圈邊沒有與磁通量發生鏈結,並且線圈邊與磁通量平行移動。因此,線上圈中沒有感應電動勢。
位置6 - 線圈邊在相反極性磁極下移動,因此感應電動勢的極性反轉。最大電動勢將在此方向上在位置7感應,而在位置1時為零。這個迴圈隨著線圈的旋轉而重複。
這樣,就在直流發電機中感應出電動勢。儘管這種感應電動勢本質上是交流電,但隨後可以使用稱為換向器的裝置將其轉換為單向電動勢。
直流發電機電樞導體中感應電動勢的方向由弗萊明右手定則 (FRHR) 決定,我們在本教程的 *模組 1(基本概念)* 中討論過。
直流發電機的電動勢方程
給出直流發電機中產生的電動勢大小的表示式稱為直流發電機的電動勢方程。我們現在將推匯出直流發電機中感應電動勢的表示式。
設:
$\phi$ = 每極磁通
*P* = 發電機的極數
*Z* = 電樞導體數
*A* = 並聯支路數
*N* = 電樞轉速 (RPM)
*E* = 產生的電動勢
因此,電樞一次旋轉時一個導體切割的磁通量(以韋伯為單位)由下式給出:
$${\mathrm{\mathit{d\phi \:=\:P\times \phi }}}$$
如果 N 是每分鐘的轉數,則完成一次旋轉所需的時間(以秒為單位)為:
$${\mathrm{\mathit{dt \:=\frac{60}{N}}}}$$
根據法拉第電磁感應定律,每個導體感應的電動勢由下式給出:
$${\mathrm{\mathrm{每導體電動勢}\:=\:\mathit{\frac{d\phi }{dt}}\:=\:\frac{\mathit{P\phi }}{\mathrm{\left ( {60/\mathit{N}} \right )}}\:=\:\frac{\mathit{P\phi N}}{\mathrm{60}}}}$$
發電機產生的總電動勢等於每個並聯支路的電動勢,它是每導體電動勢與每個並聯支路串聯導體數的乘積,即:
$${\mathrm{\mathit{E}\:=\:\left ( 每導體電動勢 \right )\times \left ( 每並聯支路導體數 \right )}}$$
$${\mathrm{\Rightarrow \mathit{E}\:=\:\frac{\mathit{P\phi N}}{60}\times \frac{\mathit{Z}}{\mathit{A}}}}$$
$${\mathrm{\therefore \mathit{E}\:=\:\frac{\mathit{NP\phi Z}}{60\mathit{A}}\:\cdot \cdot \cdot \left ( 1 \right )}}$$
公式 (1) 稱為 *直流發電機的電動勢方程*。
對於波繞組:
$${\mathrm{\mathrm{並聯支路數,}\mathit{A}\:=\:2}}$$
$${\mathrm{\therefore \mathit{E}\:=\:\frac{\mathit{NP\phi Z}}{\mathrm{120}}}}$$
對於疊繞組:
$${\mathrm{\mathrm{並聯支路數,}\mathit{A}\:=\:\mathit{P}}}$$
$${\mathrm{\therefore \mathit{E}\:=\:\frac{\mathit{N\phi Z}}{\mathrm{60}}}}$$
對於給定的直流發電機,*Z、P* 和 *A* 是常數,因此產生的電動勢 (E) 與每極磁通 ($\phi$) 和電樞旋轉速度 (*N*) 成正比。
數值例子
一臺 6 極直流發電機具有 600 個電樞導體和 0.06 Wb 的有用磁通量。如果它是波繞組連線和疊繞組連線,並且以 1000 RPM 的速度執行,則產生的電動勢是多少?
解答
已知資料:
極數,*P* = 6
電樞導體數,*Z* = 600
每極磁通量,$\phi$ = 0.06 Wb
電樞轉速,*N* = 1000 RPM
對於波繞組連線的發電機:
$${\mathrm{\mathit{E}\:=\:\frac{\mathit{NP\phi Z}}{\mathrm{120}}}}$$
$${\mathrm{\Rightarrow \mathit{E}\:=\:\frac{1000\times6\times 0.06\times 600}{120}}}$$
$${\mathrm{\therefore \mathit{E}\:=\:1800\:V}}$$
對於疊繞組連線的發電機:
$${\mathrm{\mathit{E}\:=\:\frac{\mathit{N\phi Z}}{\mathrm{60}}}}$$
$${\mathrm{\Rightarrow \mathit{E}\:=\:\frac{1000\times 0.06\times 600}{60}}}$$
$${\mathrm{\therefore \mathit{E}\:=\:600\:V}}$$
直流發電機的型別
在實際的直流發電機中,磁場是由電磁體而不是永磁體產生的。然後根據勵磁繞組在發電機電路中的連線方式對直流發電機進行分類。在此基礎上,直流發電機可分為以下兩種型別:
他勵直流發電機
自勵直流發電機
他勵直流發電機
磁場繞組由獨立的直流電源(如電池)勵磁的直流發電機稱為他勵直流發電機。圖1顯示了自勵直流發電機的連線圖。(此處應插入圖1)
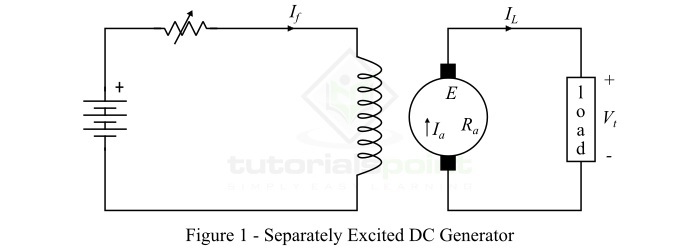
他勵直流發電機產生的電壓取決於電樞旋轉速度和勵磁電流(即電機中的磁通量)。電樞速度和勵磁電流越大,發電機中感應的電動勢越大。然而,他勵直流發電機很少用於實際應用中,因為它們需要外部直流電源進行勵磁。
自勵直流發電機
磁場繞組由發電機本身的輸出勵磁的直流發電機稱為自勵直流發電機。根據勵磁繞組與電樞的連線方式,自勵直流發電機可分為以下三種類型:
串勵直流發電機
並勵直流發電機
復勵直流發電機
串勵直流發電機
勵磁繞組與電樞串聯,使整個電樞電流流過勵磁繞組和負載的直流發電機稱為串勵直流發電機。圖2顯示了串勵直流發電機的連線圖。(此處應插入圖2)
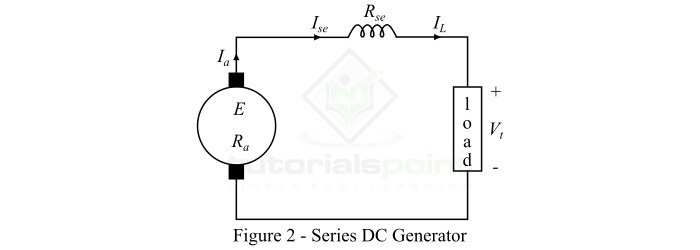
在串勵直流發電機的情況下,勵磁繞組承載整個負載電流,因此它由粗導線和少量匝陣列成,因此其電阻最小。串勵直流發電機用於提升機等特殊應用。
以下是一些串勵直流發電機的重要表示式:
$${\mathrm{\mathrm{電樞電流,}\mathit{I_{a}}\:=\:\mathit{I_{se}}\:=\:\mathit{I_{L}}}}$$
其中,$\mathit{I_{se}}$ 是串勵磁電流,$\mathit{I_{L}}$ 是負載電流。
$${\mathrm{\mathrm{端電壓,}\mathit{V_{t}}\:=\:\mathit{E-I_{a}\left ( \mathit{R_{a}+R_{se}} \right )}}}}$$
其中,*E* 是產生的電動勢,$\mathit{R_{a}}$ 是電樞電路電阻,$\mathit{R_{se}}$ 是串勵磁電阻。
並勵直流發電機
勵磁繞組與電樞繞組並聯,使發電機的端電壓加在其上的直流發電機稱為並勵直流發電機。圖3顯示了並勵直流發電機的連線圖。(此處應插入圖3)
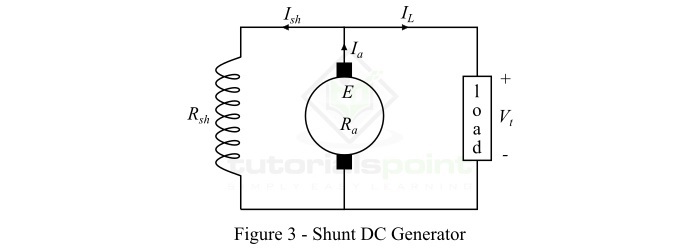
在並勵直流發電機中,並勵磁繞組具有大量細導線匝數,因此電阻較大,因此只有一部分電樞電流流過它,其餘部分流過負載。
以下是一些並勵直流發電機的重要表示式:
$${\mathrm{\mathrm{電樞電流,}\mathit{I_{a}}\:=\:\mathit{I_{L}+I_{sh}}}}$$
$${\mathrm{\mathrm{並勵磁電流,}\mathit{I_{sh}}\:=\:\frac{\mathit{V_{t}}}{\mathit{R_{sh}}}}}$$
$${\mathrm{\mathrm{端電壓,}\mathit{V_{t}}\:=\:\mathit{E-I_{a}R_{a}}}}$$
復勵直流發電機
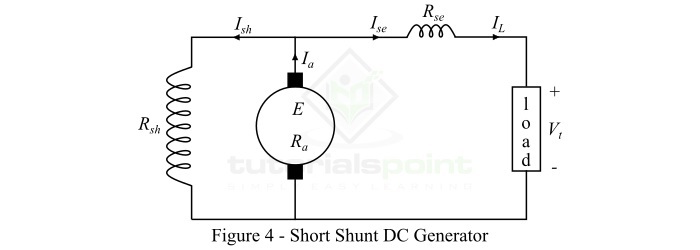
復勵直流發電機是指在每個磁極上都有兩組勵磁繞組的直流發電機——一個與電樞繞組串聯,另一個與電樞繞組並聯。復勵直流發電機可進一步分為以下兩種型別:
短 shunt 復勵直流發電機
長 shunt 復勵直流發電機
短 shunt 復勵直流發電機是指只有並勵磁繞組與電樞繞組並聯的直流發電機,如圖4所示。(此處應插入圖4)
長 shunt 復勵直流發電機是指並勵磁繞組與串勵磁繞組和電樞繞組都並聯的直流發電機,如圖5所示。(此處應插入圖5)
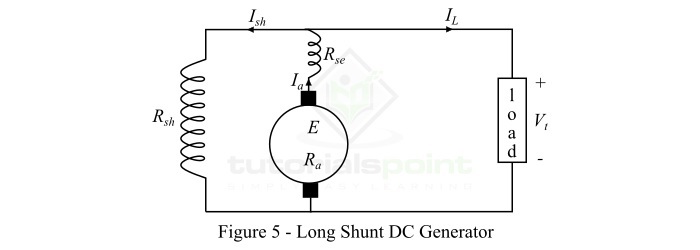
以下是復勵直流發電機的重要表示式:
對於短 shunt 發電機:
$${\mathrm{\mathrm{電樞電流,}\mathit{I_{a}}\:=\:\mathit{I_{L}+I_{sh}}}}$$
$${\mathrm{\mathrm{串勵磁電流,}\mathit{I_{se}}\:=\:\mathit{I_{L}}}}$$
$${\mathrm{\mathrm{並勵磁電流,}\mathit{I_{sh}}\:=\:\frac{\mathit{V_{t}}+\mathit{I_{se}R_{se}}}{R_{sh}}}}$$
$${\mathrm{\mathrm{端電壓,}\mathit{V_{t}}\:=\:\mathit{E-I_{a}R_{a}-I_{se}R_{se}}}}$$
對於長 shunt 發電機:
$${\mathrm{\mathrm{電樞電流,}\mathit{I_{a}}\:=\:\mathit{I_{L}+I_{sh}}}}$$
$${\mathrm{\mathrm{串勵磁電流,}\mathit{I_{se}}\:=\:\mathit{I_{a}}}}$$
$${\mathrm{\mathrm{並勵磁電流,}\mathit{I_{sh}}\:=\:\frac{\mathit{V_{t}}}{\mathit{R_{sh}}}}}$$
$${\mathrm{\mathrm{端電壓,}\mathit{V_{t}}\:=\:\mathit{E-I_{a}}\left ( \mathit{R_{a}+R_{se}} \right )}}$$
直流電機的原理
直流發電機的執行原理基於法拉第電磁感應定律。根據該定律,當穿過導體或線圈的磁通量發生變化時,導體或線圈中就會感應出電動勢。該感應電動勢的大小由下式給出:
$${\mathrm{\mathit{e}\:=\:\mathit{N}\frac{\mathit{d\phi }}{\mathit{dt}}\:\cdot \cdot \cdot (1)}}$$
其中,$\phi$是線圈的磁通鏈,N是線圈的匝數。
在直流發電機的情況下,磁通量 ($\phi$) 保持靜止,線圈旋轉。線圈旋轉而磁通靜止時感應的電動勢稱為動態感應電動勢。

為了理解直流發電機的執行原理,我們考慮一個單環直流發電機(即 *N = 1*),如圖所示。(此處應插入圖示) 此處,線圈由某個原動機(機械能的來源)旋轉,並且線圈的磁通鏈發生變化。
設 $\phi$ 為電機每個磁極產生的平均磁通量,則發電機中的平均感應電動勢由下式給出:
$${\mathrm{\mathit{E_{av}}\:=\:\frac{\mathit{d\phi }}{\mathit{dt}}\:=\:\mathrm{線圈每秒切割的磁通量}}}$$
$${\mathrm{\Rightarrow \mathit{E_{av}}\:=\:\mathrm{一次旋轉切割的磁通量\:\times \:每秒旋轉次數}}}$$
$${\mathrm{\Rightarrow \mathit{E_{av}}\:=\:\mathrm{\left ( 每極磁通量\times 極數 \right )}\:\times \:\mathrm{每秒旋轉次數}}}$$
$${\mathrm{\therefore \mathit{E_{av}}\:=\:\mathit{\phi \:\times P\:\times \:n}\:\cdot \cdot \cdot (2)}}$$
其中,*P* 是發電機的總極數,*n* 是線圈的每秒旋轉速度。公式(2)給出了單環直流發電機中的平均感應電動勢。
以下幾點解釋了直流發電機的執行原理:
位置1 - 感應電動勢為零,因為線圈邊的運動與磁通量平行。
位置2 - 線圈邊與磁通量成一定角度運動,因此在環路中產生較小的電動勢。
位置3 - 線圈邊與磁通量成直角運動,因此感應電動勢最大。
位置4 - 線圈邊以一定角度切割磁通量,因此線上圈邊中感應出較小的電動勢。
位置5 - 線圈邊沒有與磁通量發生鏈結,並且線圈邊與磁通量平行移動。因此,線上圈中沒有感應電動勢。
位置6 - 線圈邊在相反極性磁極下移動,因此感應電動勢的極性反轉。最大電動勢將在此方向上在位置7感應,而在位置1時為零。這個迴圈隨著線圈的旋轉而重複。
這樣,就在直流發電機中感應出電動勢。儘管這種感應電動勢本質上是交流電,但隨後可以使用稱為換向器的裝置將其轉換為單向電動勢。
直流發電機電樞導體中感應電動勢的方向由弗萊明右手定則 (FRHR) 決定,我們在本教程的 *模組 1(基本概念)* 中討論過。
直流電機中的反電動勢
在直流電動機中,當電樞在驅動轉矩的作用下旋轉時,電樞導體穿過磁場,因此由於發電機作用會在其中感應出電動勢。電樞導體中感應的這種電動勢與施加電壓$\mathit{V_{s}}$方向相反,被稱為反電動勢或逆電動勢。
反電動勢的大小由下式給出:
$$\mathrm{\mathit{E_{b}}\:=\:\frac{\mathit{NP\phi Z}}{\mathrm{60}\mathit{A}}\:\cdot \cdot \cdot (1)}$$
反電動勢$\mathit{E_{b}}$總是小於施加電壓$\mathit{V_{s}}$。但是,當直流電動機在正常條件下執行時,這種差異很小。
在直流電動機中,電樞中感應的反電動勢$\mathit{E_{b}}$與施加電壓相反,因此施加電壓必須克服這個電動勢$\mathit{E_{b}}$才能迫使電流$\mathit{I_{a}}$流過電樞電路以實現電機動作。克服這種阻力的所需功率由下式給出:
$$\mathrm{\mathit{P_{m}}\:=\:\mathit{E_{b}I_{a}}\:\cdot \cdot \cdot (2)}$$
功率$\mathit{P_{m}}$是實際轉換為機械功率的部分。因此,功率$\mathit{P_{m}}$也稱為機械功率的電等效值。
考慮一個其等效電路如圖1所示的並勵直流電動機。
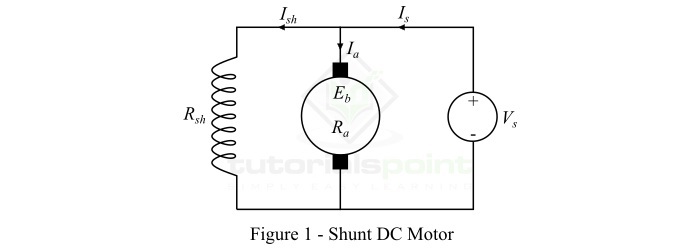
當在電動機的端子上施加直流電壓$\mathit{V_{s}}$時,勵磁電磁鐵被勵磁,電樞導體被供電。因此,驅動轉矩作用於電樞,電樞開始旋轉。當電樞旋轉時,在電樞導體中感應出反電動勢,該反電動勢與施加電壓$\mathit{V_{s}}$相反。施加電壓必須克服反電動勢使電流流過電樞導體。
直流電動機的電壓方程可以表示為:
$$\mathrm{\mathit{V_{s}\:=\:E_{b}+I_{a}R_{a}}\:\cdot \cdot \cdot (3)}$$
其中,$\mathit{R_{a}}$是電樞電路的電阻。
那麼,直流電動機的電樞電流由下式給出:
$$\mathrm{\mathit{I_{a}}\:=\:\frac{\mathit{V_{s}-E_{b}}}{\mathit{R_{a}}}\:\cdot \cdot \cdot (4)}$$
由於對於給定的電機,施加電壓$\mathit{V_{s}}$和電樞電阻$\mathit{R_{a}}$通常是固定的,因此$\mathit{E_{b}}$的值將決定直流電動機吸收的電流。如果直流電動機的速度很高,則反電動勢的值很大,因此電動機將吸收較少的電樞電流,反之亦然。
直流電動機中反電動勢的重要性
直流電動機中的反電動勢使其成為一臺自調節電機,這意味著它使電動機能夠吸收足夠的電樞電流來產生機械負載所需的轉矩。
現在,從公式(4)中,我們可以解釋反電動勢在直流電動機中的重要性如下:
情況1 - 電機空載執行
在這種情況下,直流電動機需要一個小的轉矩來克服摩擦和風阻損失。因此,電動機吸收的電樞電流$\mathit{I_{a}}$很小,反電動勢幾乎等於電源電壓。
情況2 - 電機負載突然變化
在這種情況下,當負載突然連線到電機軸上時,電樞會減速。因此,電樞導體穿過磁場的速度降低,因此反電動勢降低。降低的反電動勢允許更大的電流透過電樞導體,更大的電樞電流意味著更大的驅動轉矩。因此,很明顯,驅動轉矩隨著電機速度的降低而增加。當電樞電流足以產生機械負載所需的增加的轉矩時,電機速度的降低停止。
考慮另一種情況,其中電機的負載減小。在這種情況下,驅動轉矩暫時大於需求,因此電樞被加速。電樞速度的增加增加了反電動勢,並導致電樞電流減小。一旦電樞電流足以產生負載所需的降低的驅動轉矩,電機將停止加速。
這段討論清楚地表明,直流電動機中的反電動勢會自動調節電樞電流的流動以滿足負載要求。
直流電機的型別
在實際的直流電動機中,磁場是由電磁鐵而不是永磁體產生的。然後根據勵磁繞組在電機電路中的連線方式對直流電動機進行分類。在此基礎上,直流電動機分為以下兩種型別:
他勵直流電動機
自勵直流電動機
他勵直流電動機
磁場繞組由獨立的直流電源(如電池)勵磁的直流電動機稱為他勵直流電動機。圖1顯示了自勵直流電動機的連線圖。
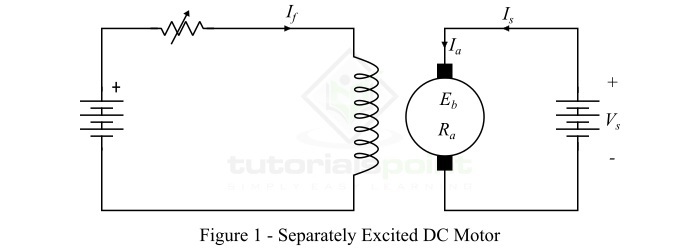
他勵直流電動機的速度取決於電源電壓和勵磁電流,即電機中的磁通量。但是,他勵直流電動機很少用於實際應用中,因為它們需要外部直流電源進行勵磁。
自勵直流電動機
磁場繞組由與電樞供電相同的電源勵磁的直流電動機稱為自勵直流電動機。
根據磁場繞組與電樞繞組的連線方式,自勵直流電動機分為以下三種類型:
串勵直流電動機
並勵直流電動機
復勵直流電動機
串勵直流電動機
磁場繞組與電樞繞組串聯,使整個電樞電流流過磁場繞組的直流電動機稱為串勵直流電動機。圖2顯示了串勵直流電動機的連線圖。
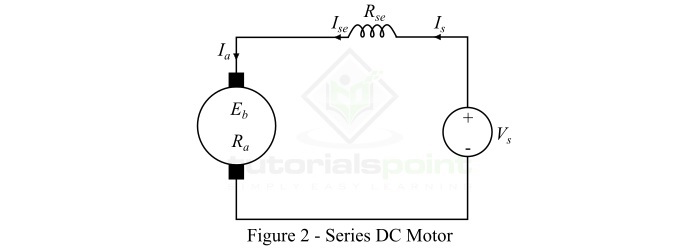
對於串勵直流電動機,磁場繞組承載整個電樞電流,因此它由較粗的線圈和較少的匝陣列成,以便具有最小的電阻。
以下是串勵直流電動機的一些重要表示式:
$$\mathrm{\mathrm{電樞電流},\mathit{I_{a}}\:=\:\mathit{I_{se}}\:=\:\mathit{I_{s}}}$$
其中,$\mathit{I_{se}}$是串勵磁電流,$\mathit{I_{s}}$是電源電流。
$$\mathrm{\mathrm{電源電壓},\mathit{V_{s}}\:=\:\mathit{E_{b}+I_{a}\left ( \mathit{R_{a}+R_{se}} \right )}}$$
其中,$\mathit{E_{b}}$是反電動勢,$\mathit{R_{a}}$是電樞電路電阻,$\mathit{R_{se}}$是串勵磁電阻。
並勵直流電動機
磁場繞組與電樞繞組並聯,使總電源電壓施加在其上的直流電動機稱為並勵直流電動機。圖3顯示了並勵直流電動機的連線圖。
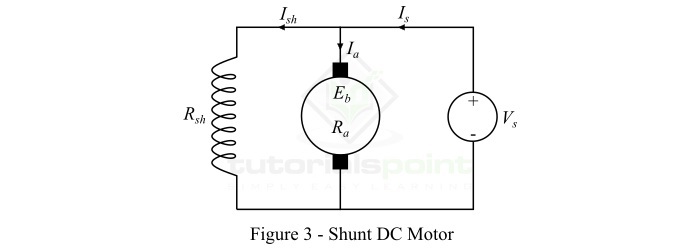
在並勵直流電動機中,並勵磁繞組具有大量細線圈,因此電阻很大,因此只有一部分電源電流流過它,其餘部分流過電樞繞組。
以下是並勵直流電動機的重要表示式:
$$\mathrm{\mathrm{電樞電流,}\mathit{I_{a}}\:=\:\mathit{I_{s}-I_{sh}}}$$
$$\mathrm{\mathrm{並勵磁電流,}\mathit{I_{sh}}\:=\:\mathit{\frac{V_{s}}{R_{sh}}}}$$
$$\mathrm{\mathrm{電源電壓,}\mathit{V_{s}}\:=\:\mathit{E_{b}+I_{a}R_{a}}}$$
復勵直流電動機
復勵直流電動機是指在每個磁極上都有兩組磁場繞組的電動機——一個與電樞繞組串聯,另一個與電樞繞組並聯。
復勵直流電動機細分為以下兩種型別:
短 shunt 復勵直流電動機
長 shunt 復勵直流電動機
短 shunt 復勵直流電動機是指只有並勵磁繞組與電樞繞組並聯的電動機,如圖4所示。
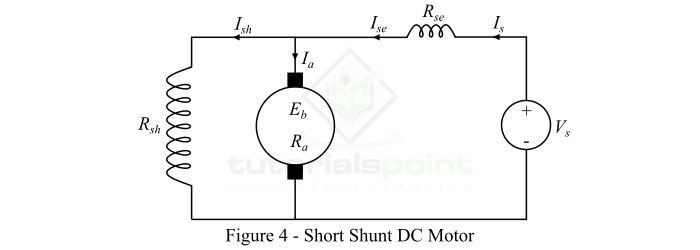
長 shunt 復勵直流電動機是指並勵磁繞組與串勵磁繞組和電樞繞組都並聯的電動機,如圖5所示。
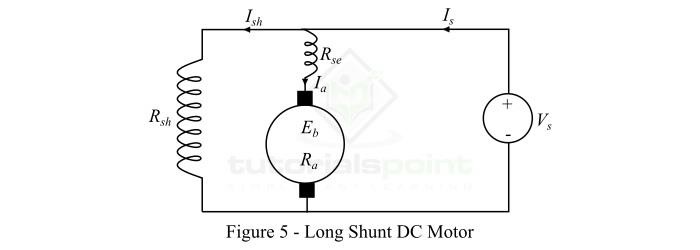
以下是復勵直流電動機的重要表示式:
對於短 shunt 電機,
$$\mathrm{\mathrm{電樞電流,}\mathit{I_{a}}\:=\:\mathit{I_{s}-I_{sh}}}$$
$${\mathrm{\mathrm{串勵磁電流,}\mathit{I_{se}}\:=\:\mathit{I_{a}}}}$$
$$\mathrm{\mathrm{並勵磁電流,}\mathit{I_{sh}}\:=\:\frac{\mathit{V_{s}}-\mathit{I_{se}R_{se}}}{R_{sh}}}$$
$$\mathrm{\mathrm{電源電壓},\mathit{V_{s}}\:=\:\mathit{E_{b}+I_{a}R_{a}+I_{se}R_{se}}}$$
對於長 shunt 電機,
$$\mathrm{\mathrm{電樞電流,}\mathit{I_{a}}\:=\:\mathit{I_{s}-I_{sh}}}$$
$$\mathrm{\mathrm{串勵磁電流,}\mathit{I_{se}}\:=\:\mathit{I_{s}}}$$
$$\mathrm{\mathrm{並勵磁電流,}\mathit{I_{sh}}\:=\:\frac{\mathit{V_{s}}}{R_{sh}}}$$
$$\mathrm{\mathrm{電源電壓},\mathit{V_{s}}\:=\:\mathit{E_{b}+I_{a}\left ( R_{a}+R_{se} \right )}}$$
直流電機的損耗
在直流電機(發電機或電動機)中,損耗可分為三類,即:
銅損
鐵損或鐵芯損耗
機械損耗
所有這些損耗都以熱量的形式出現,從而提高了機器的溫度。它們還會降低機器的效率。
銅損
在直流電機中,由於電機各種繞組的電阻而發生的損耗稱為銅損。銅損也稱為I2R損耗,因為這些損耗是由於電流流過繞組的電阻而發生的。
直流電機中發生的 主要銅損如下:
$$\mathrm{\mathrm{電樞銅損}\:=\:\mathit{I_{a}^{\mathrm{2}}R_{a}}}$$
$$\mathrm{\mathrm{串勵磁銅損}\:=\:\mathit{I_{se}^{\mathrm{2}}R_{se}}}$$
$$\mathrm{\mathrm{並勵磁銅損}\:=\:\mathit{I_{sh}^{\mathrm{2}}R_{sh}}}$$
在直流電機中,由於電刷接觸電阻,還會產生電刷接觸損耗。在實際計算中,這種損耗通常包含在電樞銅損中。
鐵損
鐵損是由於電樞在磁場中旋轉而在直流電機電樞鐵芯中發生的。因為這些損耗發生在電樞鐵芯中,所以也稱為鐵芯損耗。
鐵損或鐵芯損耗有兩種型別,即磁滯損耗和渦流損耗。
磁滯損耗
當電樞在不同極性的連續磁極下透過時,由於電樞鐵芯中的磁場反轉而在直流電機電樞鐵芯中發生的鐵芯損耗稱為磁滯損耗。磁滯損耗由以下經驗公式給出:
$$\mathrm{\mathrm{磁滯損耗,}\mathit{P_{h}}\:=\:\mathit{k_{h}B_{max}^{\mathrm{1.6}}fV}}$$
其中,$\mathit{k_{h}}$是斯坦梅茨磁滯係數,$\mathit{B_{max}}$是最大磁通密度,f是磁場反轉頻率,V是電樞鐵芯的體積。
可以透過使電樞鐵芯採用斯坦梅茨磁滯係數較低的材料(如矽鋼)來降低直流電機中的磁滯損耗。
渦流損耗
當直流電機電樞在磁極的磁場中旋轉時,會在電樞鐵心中感應出電動勢,並在其中產生渦流。由於這些渦流引起的功率損耗稱為**渦流損耗**。
$$ \mathrm{渦流損耗,} \mathit{P_{e}} = \mathit{k_{e}B_{max}^{2}f^{2}t^{2}V} $$
其中,$\mathit{K_{e}}$是比例常數,t是疊片厚度。
從渦流損耗的表示式可以看出,渦流損耗取決於疊片厚度的平方。因此,為了減少這種損耗,電樞鐵心是由薄疊片構成,這些疊片之間用一層薄薄的清漆絕緣。
機械損耗
直流電機中由於摩擦和風阻引起的功率損耗稱為**機械損耗**。在直流電機中,摩擦損耗以軸承摩擦、電刷摩擦等形式出現,而風阻損耗是由於旋轉電樞的空氣摩擦引起的。
機械損耗取決於電機的轉速。但在給定轉速下,這些損耗實際上是恆定的。
**注意**——鐵損或鐵芯損耗和機械損耗一起稱為**雜散損耗**。
恆定損耗和可變損耗
在直流電機中,我們可以將上述討論的損耗分為以下兩類:
恆定損耗
可變損耗
直流電機中在所有負載下保持恆定的損耗稱為**恆定損耗**。這些損耗包括:*鐵損、勵磁繞組銅損和機械損耗*。
直流電機中隨負載變化的損耗稱為**可變損耗**。直流電機的可變損耗包括:電樞銅損和串勵繞組銅損。
Total losses in a DC machine = Constant losses + Variable losses
直流電機的應用
目前,大量的電能以交流電的形式產生。因此,直流電機(電動機或發電機)的使用變得有限。然而,直流電機仍在一些應用中使用,例如為交流發電機的勵磁系統供電、電解過程、焊接過程等。
直流發電機的應用
不同型別直流發電機的應用如下:
他勵直流發電機
發電機主要用於實驗室的實驗和測試。
它們也用作為直流電動機供電的直流電源。
串勵直流發電機
串勵直流發電機用於直流機車再生制動,為勵磁電流供電。
串勵直流發電機也用作配電系統中的升壓器。
差動復勵串勵發電機用於電弧焊接。
過勵磁積性串勵發電機用於照明和重型電源。
平勵串勵發電機用於為辦公室、住宅和其他商業建築供電。
並勵直流發電機
shunt 直流發電機主要用於照明。
shunt 直流發電機用於充電電池。
這些發電機也用於為交流發電機供給勵磁電流。
直流電動機的應用
不同型別直流電動機的應用如下:
串勵直流電動機
串勵直流電動機用於需要高啟動轉矩的應用。
串勵直流電動機用於起重機和升降機。
串勵直流電動機用於電力牽引。
它們用於空氣壓縮機。
它們也用於真空吸塵器。
串勵直流電動機也用於縫紉機等。
並勵直流電動機
shunt 直流電動機用於需要恆速的應用。
shunt 直流電動機用於驅動車床。
它們也用於離心泵和鼓風機。
它們用於風扇、輸送機和紡紗機。
這些直流電動機也用於電梯。
復勵直流電動機
復勵直流電動機用於那些需要高啟動轉矩和恆速的應用。
用於印刷機。
它們也用於剪下機。
它們用於電梯和升降機。
復勵直流電動機也用於軋機和重型刨床等。
感應電機的介紹
**感應電動機**是工業應用中最廣泛使用的電動機。幾乎所有感應電動機從空載到滿載條件下都以基本恆定的速度執行。感應電動機的速度取決於電源頻率,因此這些電動機不容易適應速度控制。感應電動機的結構簡單而堅固,價格便宜,易於維護,並且可以設計和生產出具有滿足大多數工業要求的特性。
什麼是感應電動機?
**感應電動機**是一種非同步交流電動機,它將交流電轉換成機械能。它被稱為感應電動機,因為產生驅動轉矩所需的轉子電路中的電流是透過定子繞組的旋轉磁場進行**電磁感應**獲得的。
這些電動機被稱為非同步電動機,因為它們的轉子轉速低於旋轉磁場的同步轉速。

感應電動機是一種機電能量轉換裝置,即它將電能轉換成機械能,以軸的旋轉形式出現。像任何電動機一樣,感應電動機有兩個主要部分,即**定子**和**轉子**。
定子帶有一組稱為**定子繞組**的繞組。定子繞組可以是單相繞組或三相繞組。
轉子帶有一個短路繞組,稱為**轉子繞組**。
在感應電動機中,只有定子繞組由交流電源供電,而轉子繞組透過電磁感應從定子繞組獲得電壓和功率。
感應電動機的執行原理
感應電動機的執行基於**電磁感應原理**。在感應電動機中,有兩個繞組,即 *定子繞組和轉子繞組*。輸入交流電源連線到定子繞組,流過定子繞組的電流產生磁通。這個磁通通常是旋轉的,因此也稱為旋轉磁場。感應電動機的轉子繞組是一個短路繞組。
來自定子的旋轉磁通切割轉子繞組的短路導體。根據法拉第電磁感應定律,在轉子電路中感應出電動勢,導致電流流過它。當電流流過轉子繞組時,機器中會產生另一個磁通。
因此,感應電動機內部有兩個磁通,一個是定子磁通,另一個是轉子磁通。這兩個磁通相互作用。正因為如此,轉子將受到一個轉矩,使轉子沿定子旋轉磁場的方向旋轉。就這樣,感應電動機執行。
感應電動機的型別
根據輸入電源的型別,感應電動機分為以下兩種型別:
**單相感應電動機**——在單相交流電源下工作的感應電動機稱為單相感應電動機。
**三相感應電動機**——需要三相交流電源才能執行的感應電動機稱為三相感應電動機。
感應電動機的優點
以下是感應電動機的一些主要優點:
感應電動機的結構簡單而堅固。
感應電動機的價格相對便宜。
感應電動機的效率相對較高。
感應電動機可以設計成具有滿足工業要求的特性。
感應電動機幾乎不需要維護。
感應電動機的缺點
感應電動機的主要缺點如下:
感應電動機的速度不容易改變,因為它們基本上是恆速電動機。
感應電動機在啟動時會吸收很大的湧流。
感應電動機始終在滯後功率因數下執行。
單相感應電動機不是自啟動的;因此,我們需要提供一些額外的啟動機構。
單相感應電機
顧名思義,這些感應電動機是在單相交流電源上執行的。**單相感應電動機**是最常見的電動機,因為它們通常用於家用和商用電器,如風扇、泵、洗衣機、空調、冰箱等。
雖然單相感應電動機的效率比三相感應電動機低,但它們被廣泛用作低功率應用中三相感應電動機的替代品。
典型的單相感應電動機由兩個主要部分組成——*定子*和*轉子*。單相感應電動機的定子帶有單相繞組,而轉子採用鼠籠式結構。
如何使感應電動機自啟動?
單相感應電動機的主要缺點是它不是自啟動的,而是需要某種啟動機構。在單相感應電動機中,定子繞組產生一個以正弦方式變化的脈動磁場。因此,該磁場在交流電的每個半週期後都會反轉其極性,但在空間中不會旋轉。結果,這個交變磁場不會在靜止轉子中產生旋轉。雖然,如果轉子透過某種外部手段在一個方向上旋轉,它將繼續沿旋轉方向執行。然而,這種啟動單相感應電動機的方法在實踐中並不方便。
因此,為了使單相感應電動機自啟動,我們需要以某種方式在電機內部產生旋轉磁場。這可以透過提供一個附加繞組將單相交流電源轉換為兩相交流電源來實現。因此,單相感應電動機在其定子上包含兩個繞組,即**主繞組**和**啟動繞組**。這兩個繞組彼此相差90°。
單相感應電動機的型別
根據電機自啟動方式的不同,單相感應電動機可分為以下三種類型:
分相式感應電動機
電容啟動式感應電動機
電容啟動電容執行式感應電動機
現在讓我們更詳細地討論每種感應電動機。
分相式感應電動機
分相式感應電動機是一種單相感應電動機,其定子由兩個繞組組成,即啟動繞組和主繞組,其中啟動繞組相對於主繞組電角度上相差90°。
啟動繞組僅在電機啟動期間工作。啟動繞組和主繞組的設計使得啟動繞組具有高電阻和相對低的電抗,而主繞組具有相對低的電阻和高電抗,以便兩個繞組中流動的電流具有大約25°到30°的合理相位差($\alpha$)。
現在,當電機的啟動繞組連線到單相交流電源時,啟動繞組將承載電流$\mathit{I_{s}}$,而主繞組將承載電流$\mathit{I_{m}}$,如圖1所示。
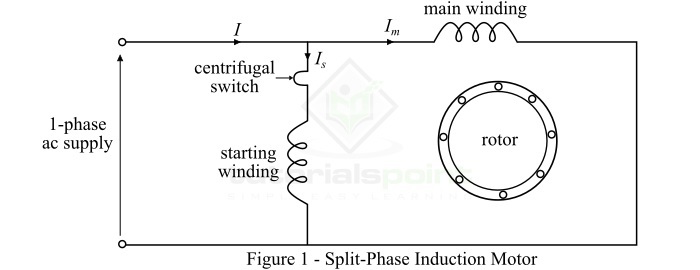
由於啟動繞組設計成高電阻,而主繞組設計成高電感。因此,兩個繞組中的電流$\mathit{I_{s}}$和$\mathit{I_{m}}$具有大約25°到30°的合理相位差。結果,在電機內部產生一個較弱的旋轉磁場,從而啟動電機。
電容啟動式感應電動機
這種型別的單相感應電動機,如圖2所示,在啟動繞組串聯連線一個電容C。這個電容稱為啟動電容。啟動電容的值選擇使得啟動電流$\mathit{I_{s}}$領先於透過主繞組的電流$\mathit{I_{m}}$約80°。
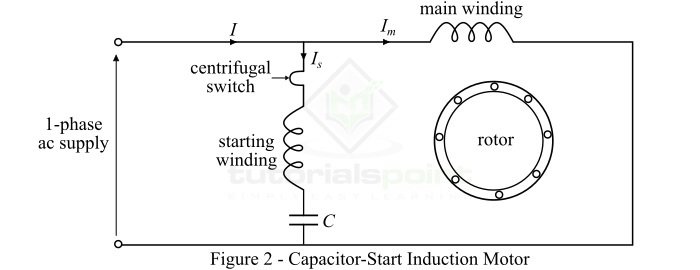
一旦電機達到額定速度的約75%,離心開關就會將啟動繞組與電路隔離。然後,電機作為單相感應電動機執行,並繼續加速直到達到正常速度。因此,在這種型別的單相感應電動機中,啟動繞組串聯的電容會在兩個繞組之間引入相移,以便電機能夠自行啟動。
電容啟動電容執行式感應電動機
這種電機與電容啟動式感應電動機幾乎相同,只是啟動繞組不會與電機電路斷開。因此,對於電容啟動電容執行式感應電動機,啟動和執行期間,兩個繞組(啟動繞組和主繞組)都保持連線到電源。
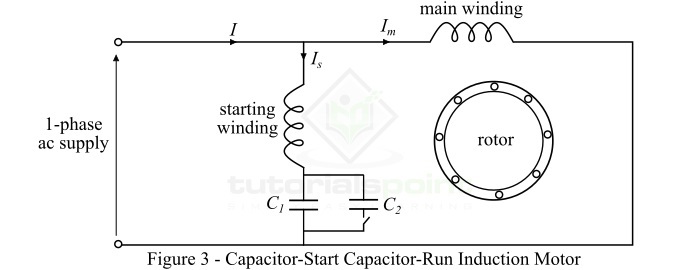
在這種電機中,啟動繞組使用兩個電容C1和C2,如圖3所示。電容C1具有較小的電容值,用於電機的最佳執行,因此永久地與啟動繞組串聯連線,而較大的電容C2與C1並聯連線,並且它僅在啟動期間保持在電路中。當電機達到額定速度的約75%時,離心開關將啟動電容C2與電路隔離。然後電機作為單相感應電動機執行。
單相感應電機的應用
單相感應電動機主要用於家用和商用電器,如風扇、空調、冰箱、空氣冷卻器、洗衣機等。以下是各種單相感應電動機的一些應用:
分相式感應電動機——這些電機最適合中等啟動轉矩的應用,例如風扇、洗衣機、燃油燃燒器、小型機床等。
電容啟動式感應電動機——這些電機適用於需要相對較高的啟動轉矩的應用,例如壓縮機、大型風扇、泵和高慣性負載等。
電容啟動電容執行式感應電動機——這些電機適用於恆轉矩和無振動的應用,例如醫院裝置、錄音棚裝置以及許多其他需要安靜執行的裝置。
三相感應電機
顧名思義,三相感應電動機是一種使用三相交流電源工作的電動機,它將三相交流電轉換為機械能。三相感應電動機是工業中最廣泛使用的電動機。這些電機的速度從空載到滿載幾乎恆定,即它們具有良好的調速效能。雖然三相感應電機的速度取決於電源頻率和電機中的極數,因此很難改變其速度。
與任何其他電動機一樣,典型的三相感應電動機也由兩個主要部分組成,即定子和轉子。定子是靜止部分,並帶有三相繞組,稱為定子繞組。轉子是電機的旋轉部分,並帶有短路繞組,稱為轉子繞組。
三相感應電機的定子繞組由三相平衡交流電源供電,而轉子繞組透過電磁感應從定子繞組獲得工作電壓和功率。這就是它被如此命名的原因。
三相感應電動機可以被認為是具有旋轉次級繞組的三相變壓器。因此,它可以被描述為一種變壓器型交流電機。唯一的區別在於感應電動機將電能轉換為機械能。
三相感應電機的型別
根據轉子結構的不同,三相感應電動機可分為以下兩種基本型別:
鼠籠式感應電動機
滑環式感應電動機
三相感應電機的優點
以下是三相感應電動機的一些主要優點:
三相感應電機的設計和製造非常簡單。
它們具有堅固的結構。
三相感應電動機需要較少的維護。
三相感應電動機具有自啟動特性。
這些電機具有相當好的功率因數。
三相感應電動機更經濟。
它們具有高效率。
三相感應電機的缺點
三相感應電機的主要缺點如下:
三相感應電動機基本上是恆速電機,需要複雜的機構來改變速度。
三相感應電動機始終工作在滯後功率因數下。
這些電機啟動電流非常高。
三相感應電機的應用
三相感應電機的主要應用如下:
鼠籠式三相感應電動機適用於驅動鼓風機、風扇、機床、離心泵等。
三相感應電動機也用於驅動不同的工業負載,如壓縮機、破碎機、輸送機、往復泵等。
滑環式感應電動機最適合驅動需要高啟動轉矩的負載,如破碎機、柱塞、起重機、電梯、提升機、輸送機等。
三相感應電機的構造
三相感應電動機由兩個主要部分組成,即:
定子
轉子
定子和轉子之間有一個小的氣隙,其範圍為0.4毫米到4毫米,具體取決於電機的額定功率。
定子
三相感應電機的定子是靜止部分,它由一個由鋼板製成的圓柱形框架組成。這個鋼製框架封閉著一個由矽鋼薄疊片組成的空心圓柱形鐵芯。在鐵芯的內周,設定了許多均勻間隔的槽,用於放置定子繞組。矽鋼疊片用於減少磁滯和渦流損耗。

三個繞組放置在定子槽中,並適當地連線以形成平衡的三相三角形或星形連線電路。根據電機速度的要求,這三個繞組繞製成一定的極數。其中,極數越多,感應電機的速度越低,反之亦然。
當我們用平衡的三相電源供電給三相定子繞組時,就會產生一個幅值恆定的旋轉磁場。這個旋轉磁場透過電磁感應在轉子電路中感應電動勢。
轉子
轉子是三相感應電機的旋轉或移動部分。它由一個由優質矽鋼薄疊片製成的轉子鐵芯組成,以減少磁滯和渦流損耗。轉子鐵芯是一個空心圓柱體,安裝在軸上。在轉子鐵芯的外周,設定了槽,用於放置轉子繞組。
根據結構的不同,三相感應電機的轉子可以是以下兩種型別:
鼠籠式轉子
繞線式轉子
讓我們詳細討論這兩種型別的轉子。
鼠籠式轉子
鼠籠式轉子由一個疊片圓柱形鐵芯組成,其外周具有平行槽。對於鼠籠式轉子,轉子繞組由金屬(銅或鋁)條組成。這些金屬條放置在轉子槽中,並在每端由稱為端環的金屬環短路,如圖2所示。

從圖2可以看出,這種轉子的結構類似於松鼠籠,因此得名。這裡還要注意的是,轉子沒有與電源電連線,而是透過電磁感應從定子獲得電壓和功率。
採用鼠籠式轉子的三相感應電動機被稱為鼠籠式感應電動機。由於其簡單而堅固的結構使其能夠在大多數惡劣環境下執行,因此在工業應用中使用的三相感應電動機中,有70%到80%是鼠籠式感應電動機。儘管使用鼠籠式轉子的感應電動機啟動轉矩較低。
繞線式轉子
繞線式轉子由一個由矽鋼製成的疊片圓柱形鐵芯組成。它帶有類似於定子繞組的三相轉子繞組,如圖3所示。

繞線式轉子的轉子繞組均勻地分佈在槽中,並以星形方式連線。星形連線的轉子繞組的開口端被引出並連線到安裝在轉子軸上的三個滑環。一個碳刷接觸在每個滑環上,並且透過這些碳刷,可以將外部電阻新增到轉子電路中。
啟動時,在轉子繞組的各相中加入合適的外部電阻,以獲得較高的啟動轉矩。隨著電動機加速到額定速度,這些外部電阻會逐漸從電路中移除。使用外部電阻可以顯著降低啟動電流並提高電動機的啟動轉矩。一旦電動機達到正常速度,三個碳刷短路,使繞線式電動機像鼠籠式感應電動機一樣執行。
三相感應電機負載執行
本章將解釋三相非同步電動機帶負載時的執行特性。
當我們將機械負載連線到三相非同步電動機的轉子軸上時,轉子將開始減速,因此旋轉磁場 (RMF) 將以更高的速率切割轉子導體。因此,轉子導體中的感應電動勢和電流將逐漸增加,產生更大的轉矩。此轉矩加速轉子,轉子和機械負載很快就會達到平衡狀態,此時轉子轉矩和負載轉矩相等。一旦達到此狀態,電動機的速度停止進一步下降,因此電動機將以新的速度勻速執行。
然而,三相非同步電動機隨著負載增加而速度下降的幅度很小。這是因為其轉子電路的阻抗很低,速度的微小下降會產生較大的轉子電流。這種增加的轉子電流產生更大的轉矩,以滿足電動機軸上增加的負載需求。這就是為什麼三相非同步電動機被認為是恆速電動機的原因。但是,這些電動機永遠不會以同步速度執行,因此它們也稱為非同步電動機。
從技術上講,三相非同步電動機的負載變化是透過調整滑差 (同步速度和轉子速度之差) 來實現的。這意味著,隨著電動機軸上負載的增加,滑差會略微增加。因此,旋轉磁場和轉子導體之間的相對速度增加。因此,轉子電流增加,產生更大的電動機轉矩以滿足增加的負載需求。
此外,隨著機械負載的增加,增加的轉子電流的方向會降低定子的旋轉磁通 (根據楞次定律),從而降低定子繞組的反電動勢。反電動勢的降低允許定子電流增加,從而增加感應電動機的輸入功率。
感應電動機的滑差概念
在三相非同步電動機中,轉子永遠無法達到定子旋轉磁場的速度 (稱為同步速度)。如果達到同步速度,旋轉磁場和轉子導體之間就不會有相對運動,轉子導體中就不會有感應電動勢,因此也就沒有轉矩來旋轉轉子。因此,實際上,感應電動機的轉子速度總是小於同步速度。這種差異稱為滑差速度,即:
$$ \mathrm{滑差速度} = N_{s} - N_{r} $$
其中,$N_{s}$ 是同步速度,$N_{r}$ 是轉子速度。
$$ \mathrm{同步速度,} N_{s} = \frac{120f}{P} $$
其中,f 是電源頻率,P 是感應電動機的極數。
滑差速度與同步速度的比率稱為感應電動機的滑差,即:
$$ \mathrm{滑差,} s = \frac{N_{s} - N_{r}}{N_{s}} $$
此外,
$$ \mathrm{滑差百分比,} s = \frac{N_{s} - N_{r}}{N_{s}} \times 100\% $$
在實際的三相非同步電動機中,從空載到滿載的滑差變化約為 0.1% 到 3%。
數值例子
一個 8 極 3 相感應電動機連線到 60 Hz 電源。如果它以 880 RPM 的速度執行。計算滑差。
解答
已知資料:
極數,P = 8
頻率,f = 60 Hz
轉子速度,Nr = 880 RPM
$$ \mathrm{因此同步速度,} N_{s} = \frac{120 \times 60}{8} = 900 $$
因此,滑差為:
$$ \mathrm{滑差,} s = \frac{900 - 880}{900} \times 100 = 2.22\% $$
三相感應電機的特性
三相非同步電動機的執行效能可以用以下兩個特性來解釋:
轉矩-滑差特性
轉矩-速度特性
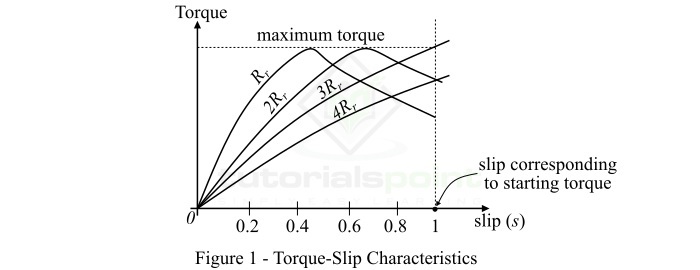
三相非同步電動機的轉矩-滑差特性
三相非同步電動機的轉矩-滑差特性是在特定轉子電阻值下,電動機轉矩與滑差之間繪製的曲線。圖 1 顯示了典型三相非同步電動機的不同轉矩-滑差特性,滑差範圍為 s = 0 到 s = 1,轉子電阻值為各種不同的值。
對於三相非同步電動機,執行條件下電動機轉矩與滑差之間的關係由下式給出:
$$ \tau_{r} = \frac{KsR_{r}}{R_{r}^{2} + s^{2}X_{r}^{2}} \cdots (1) $$
其中,K 是常數,s 是滑差,$R_{r}$ 是每相轉子電阻,$X_{r}$ 是每相靜止轉子電抗。
從公式 (1) 中,我們可以得出以下幾點:
情況 1
如果 s = 0,則 $\tau_{r} = 0$。因此,轉矩-滑差曲線從原點開始。
情況 2
在電動機的正常速度下,滑差很小,因此 $sX_{r}$ 與 $R_{r}$ 相比實際上可以忽略不計。
$$ \tau_{r} \propto \frac{s}{R_{r}} $$
由於對於給定的電動機,$R_{r}$ 也是常數。
$$ \tau_{r} \propto s $$
因此,轉矩-滑差曲線是從零滑差到對應於滿載滑差的直線。
情況 3
如果滑差值超過滿載滑差,則轉矩增加並在 $R_{r} = sX_{r}$ 時達到最大值。三相非同步電動機中的這個最大轉矩稱為擊穿轉矩或最大轉矩。當感應電動機在額定電壓和頻率下執行時,擊穿轉矩的值至少是滿載轉矩的兩倍。
情況 4
當滑差值大於對應於最大轉矩的滑差值時,$s^{2}X_{r}^{2}$ 項迅速增加,因此可以忽略 $R_{r}^{2}$。
$$ \tau_{r} \propto \frac{s}{s^{2}X_{r}^{2}} $$
由於 $X_{r}^{2}$ 實際上是常數,則
$$ \tau_{r} \propto \frac{1}{s} $$
因此,轉矩現在與滑差成反比。因此,轉矩-滑差曲線是矩形雙曲線。
因此,從以上對三相非同步電動機轉矩-滑差特性的分析可以看出,向轉子電路中新增電阻不會改變最大轉矩的值,而只會改變發生最大轉矩的滑差值。
三相非同步電動機的轉矩-速度特性
對於三相非同步電動機,電動機轉矩取決於速度,但我們無法用簡單的數學方程來表示它們之間的關係。因此,我們使用轉矩-速度特性曲線來顯示這種關係。圖 2 顯示了三相非同步電動機的典型轉矩-速度特性曲線。
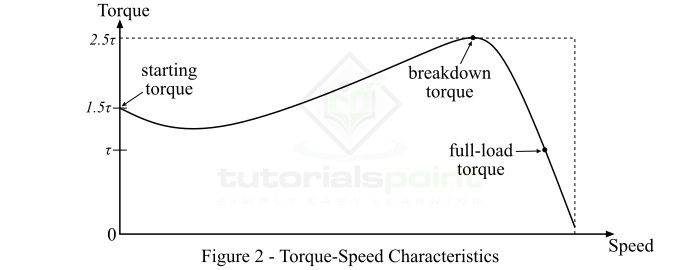
從該特性曲線中可以注意到以下幾點:
如果滿載轉矩為 $\tau$,則啟動轉矩為 $1.5\tau$,最大轉矩(或擊穿轉矩)為 $2.5\tau$
在滿載情況下,如果電動機的速度為 N,如果軸上的機械負載增加,則電動機的速度將下降,直到電動機轉矩再次等於負載轉矩。一旦兩個轉矩相等,電動機將以恆定速度執行,但低於之前的速度。但是,如果電動機轉矩大於 $2.5\tau$(即擊穿轉矩),則電動機將突然停止。
對於三相非同步電動機,轉矩-速度曲線在空載點和滿載點之間基本上是一條直線。曲線線的斜率取決於轉子電路的電阻,即電阻越大,斜率越陡峭。
調速和速度控制
感應電動機的速度調節
感應電動機的速度調節定義為電動機速度隨負載變化而變化的程度。它表示為滿載速度的分數或百分比,即:
$$ \mathrm{速度調節} = \frac{N_{nl} - N_{fl}}{N_{fl}} \times 100\% $$
其中,$N_{nl}$ 是電動機的空載速度,$N_{fl}$ 是電動機的滿載速度。
感應電動機的速度調節約為 3% 到 5%。由於這種小的速度調節,感應電動機被歸類為恆速電動機。
三相非同步電動機的速度控制
三相非同步電動機的速度由下式給出:
$$ N_{r} = (1 - s)N_{s} \cdots (1) $$
其中,s 是滑差,$N_{s}$ 是以 RPM 表示的同步速度。
$$ N_{s} = \frac{120f}{P} \cdots (2) $$
從公式 (1) 和 (2) 可以看出,可以透過改變以下引數來改變三相非同步電動機的速度:
交流電源的頻率 (f),
定子極數 (P),以及
滑差 (s)。
實際上,通常無法改變電源頻率,因為商用電力供應的頻率是恆定的。因此,可以透過改變定子極數 (P) 或滑差 (s) 來改變三相非同步電動機的速度。我們現在將討論鼠籠式和滑環式感應電動機的速度控制。
鼠籠式感應電動機的速度控制
鼠籠式感應電動機的速度控制是透過改變定子極數來改變的。透過改變極數的方法,只有兩種或四種速度是可能的。
在兩速感應電動機中,提供一個定子繞組,可以透過合適的控制裝置進行切換以提供兩種速度。其中一種速度是另一種速度的一半。例如,定子繞組可以連線到 4 個或 8 個定子極,當電動機由 50 Hz 交流電源供電時,同步速度分別為 1500 RPM 和 750 RPM。
在四速感應電動機中,提供兩個獨立的定子繞組,每個繞組提供兩種速度。
以下是改變極數速度控制方法的主要缺點:
此方法不能用於獲得逐漸連續的速度控制。
它使電動機的設計和定子繞組互連的切換更加複雜。
由於設計和互連的複雜性,此方法最多隻能為任何一臺電動機提供四種不同的速度。
滑環式感應電動機的速度控制
可以透過改變電動機滑差來改變滑環式感應電動機的速度。採用以下方法來改變滑差,從而改變速度:
透過改變定子線電壓。
透過改變轉子電路的電阻。
透過在轉子電路中新增和改變外加電壓。
數值例子
對於三相非同步電動機,電動機的空載速度為 900 RPM,滿載速度為 880 RPM。求電動機的速度調節。
解答
已知資料:
$N_{nl}$ = 900 RPM
$N_{fl}$ = 880 RPM
$$ \mathrm{速度調節} = \frac{N_{nl} - N_{fl}}{N_{fl}} \times 100\% $$
$$ \mathrm{速度調節} = \frac{900 - 880}{880} \times 100\% = 2.273\% $$
三相感應電機的啟動方法
以下四種方法廣泛用於啟動三相非同步電動機:
直啟動器
自耦變壓器啟動器
星-三角啟動器
轉子電阻啟動器
本章將詳細討論每種啟動方法。
直啟動器
顧名思義,直啟動器 (D.O.L.) 指的是將三相感應電動機直接連線到三相平衡交流電源上啟動的方法,如圖 1 所示。
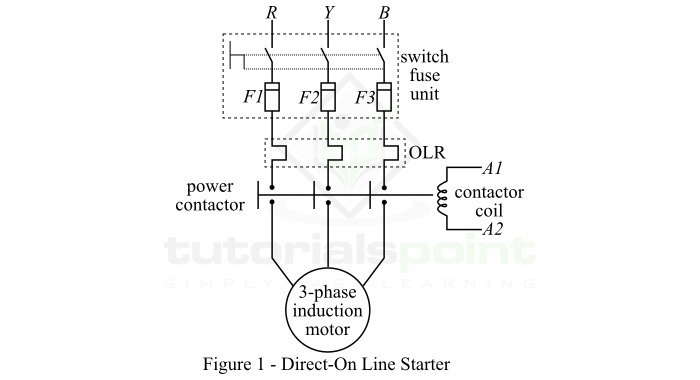
在這種方法中,感應電動機將吸收非常高的啟動電流,大約是額定電流的 4 到 10 倍。這是因為電動機靜止時的阻抗很低。因此,直啟動 (D.O.L.) 方法適用於低功率等級的電動機,通常功率等級不超過 7.5 kW。
自耦變壓器啟動器
在這種感應電動機啟動方法中,使用三相自耦變壓器向電動機提供三相電力。自耦變壓器主要用於降低啟動時的電源電壓,然後在電動機達到足夠的速度後將其連線到全電壓電源。
自耦變壓器啟動器的電路佈置如圖 2 所示。用於啟動感應電動機的自耦變壓器上的抽頭設定方式為:當它連線到電路中時,向電動機施加 60% 到 80% 的電源電壓。
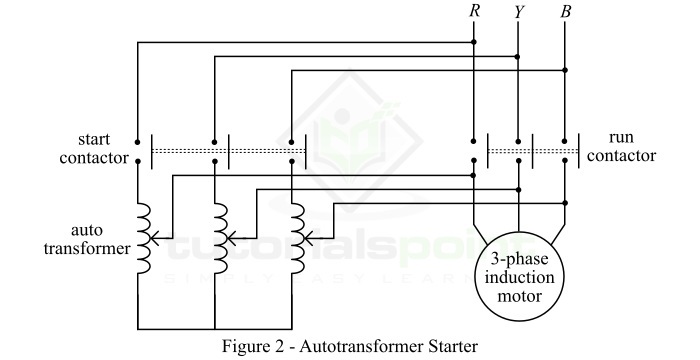
啟動瞬間,自耦變壓器接入電路,從而降低了施加到電動機的電壓。因此,啟動電流被限制在一個安全值內。當電動機達到額定速度的約 80% 時,透過轉換開關將自耦變壓器從電路中移除,然後將電動機連線到全電壓電源。自耦變壓器啟動器具有功率損耗低、啟動電流小等優點。因此,這種方法適用於功率等級超過 25 馬力的較大感應電動機。
星-三角啟動器
在這種方法中,三相感應電動機以星形連線方式啟動,然後以三角形連線方式執行。
採用星-三角啟動器的感應電動機的定子繞組設計為三角形執行,並在啟動期間連線成星形。當電動機達到足夠的速度時,繞組連線將從星形改為三角形。
圖 3 顯示了星-三角啟動器的電路佈置。這裡,定子繞組的六個端子連線到一個轉換開關。啟動瞬間,轉換開關將定子繞組連線成星形配置。結果,每個定子相位獲得等於 *V/*√3 的電壓,其中 *V* 是全線電壓。這樣,在啟動期間,定子繞組獲得降低的電壓。
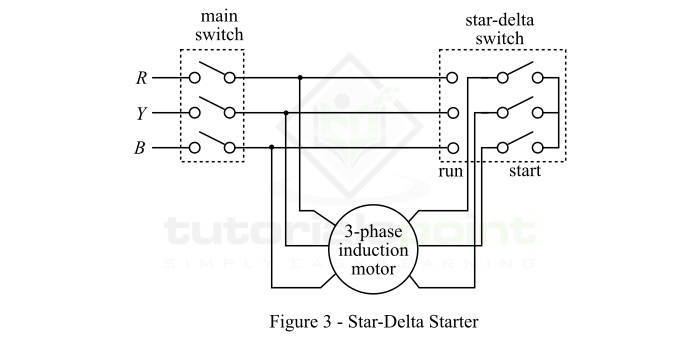
當電動機達到特定速度時,轉換開關將定子繞組的連線改為三角形。每個相位現在獲得全線電壓 V,並且電動機以正常速度執行。然而,這種三相感應電動機的啟動方法會導致電動機的啟動轉矩大幅降低。這種方法最適合中等尺寸的感應電動機,功率等級不超過約 25 馬力。
轉子電阻啟動器
這種啟動方法僅適用於滑環感應電動機。在這種方法中,一個可變星形連線的電阻器透過滑環插入轉子電路,並將全電壓施加到定子繞組。轉子電阻啟動器的電路佈置如圖 4 所示。
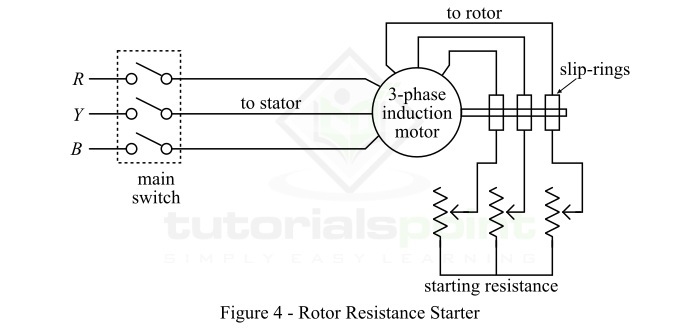
啟動瞬間,星形連線電阻器的旋鈕設定為“關閉”位置。因此,在轉子電路的每個相位中插入最大電阻,從而降低啟動電流。同時,該電阻會增加啟動轉矩。
當電動機加速時,透過移動電阻器旋鈕,逐漸從轉子電路中去除外部電阻。一旦電動機達到正常速度的約 80%,將旋鈕切換到“開啟”位置,從而將所有外部電阻從轉子電路中移除。
三相同步電機的介紹
以同步速度(即旋轉磁場的速度)執行的機電能量轉換裝置(或電機)被稱為**同步電機**。同步電機是一種交流電機,即它需要交流電源才能工作。
根據能量轉換,同步電機可分為兩種型別:
同步發電機
同步電動機
同步電機是電力系統應用中使用最廣泛的電機,例如發電機、功率因數校正、驅動恆速機械負載等。
將機械能轉換為交流電的同步電機稱為**同步發電機**或**交流發電機**。而將交流電轉換為機械能的同步電機稱為**同步電動機**。
在大多數實際應用中使用的同步電機是三相交流電機。然而,也存在單相同步電機,但它們僅用於特殊應用。
同步電機(發電機或電動機)始終以恆定的速度執行,稱為同步速度。**同步速度**由以下關係式給出:
$$ \mathrm{\mathit{N_{s}}\:=\:\frac{120\mathit{f}}{\mathit{p}}\cdot \cdot \cdot (1)} $$
其中:
**f** 是電源頻率,
**P** 是電機中的極數。
同步速度以每分鐘轉數 (RPM) 測量。
為了獲得令人滿意的執行,同步電機始終保持公式 (1) 中給出的表示式。如果同步電機未能保持公式 (1) 中的上述關係,則電機將停止執行,這種情況稱為電機的**失去同步**或**失步**。因此,這證明了同步電機設計為以恆定速度執行。
同步電機的執行原理
同步電機的執行原理基於**電磁相互作用定律**和**磁互鎖定律**。
根據電磁相互作用定律,當導體和磁場之間存在相對運動時,導體中會感應出電動勢。另一方面,當載流導體放置在磁場中時,導體上會作用一個力,該力趨於使其移動。
根據磁互鎖定律,兩個不同的磁場(定子的磁場和轉子的磁場)相互鎖定並以相同的速度旋轉。這種現象稱為**磁互鎖**。
這兩個原理解釋了同步電機的執行方式。同步電機首先透過電磁相互作用啟動,然後轉子和定子的磁場鎖定在一起,以同步速度旋轉。
三相同步發電機
透過電磁感應將機械能轉換為三相電能的同步電機稱為**三相同步發電機**或**交流發電機**。
三相交流發電機由電樞繞組和勵磁繞組組成,其中在電樞繞組中感應電動勢,而勵磁繞組產生工作磁場。對於三相交流發電機,電樞繞組設定在電機的定子部分,而勵磁繞組設定在轉子上。靜止電樞繞組的主要優點是無需像直流發電機那樣需要換向器。
三相同步發電機最廣泛地用於發電廠發電。
三相同步電動機
將三相電能轉換為機械能的同步電機稱為**三相同步電動機**。
與任何其他電動機一樣,同步電動機也包括兩個主要部分,即定子和轉子。定子帶有三相電樞繞組,而轉子帶有勵磁繞組,勵磁繞組由直流電源勵磁以產生一定數量的固定磁極。
同步電動機的獨特之處在於它可以以恆定的速度執行,稱為同步速度。然而,三相同步電動機的主要缺點是它沒有自啟動轉矩。因此,為了啟動三相同步電動機,必須透過某種輔助手段將其速度提高到接近其同步速度。
作為恆速電動機,電動機上的負載不超過極限值。如果電動機上的負載超過極限值,電動機將立即停止執行。三相同步電動機用於:以恆定速度驅動機械負載,提高系統的功率因數等。
同步電機的特點
以下是同步電機(電動機或發電機)的關鍵特徵:
同步電動機沒有自啟動轉矩。
同步電機是雙勵磁電機,因為它需要兩個輸入電源——一個在定子上,另一個在轉子上。
同步電機以恆定速度執行,稱為同步速度。
同步發電機可以產生幅度和頻率恆定的電壓。
同步電機可以透過改變勵磁來以滯後、超前或單位功率因數執行。
與感應電動機相比,同步電動機的啟動轉矩相對較高。
同步電動機適用於驅動恆定和低速(通常小於 300 RPM)負載。
同步電機價格昂貴。
同步電機的構造
與任何其他旋轉電機一樣,同步電機(發電機或電動機)有兩個基本部件:
**定子**——它是電機的靜止部分,並帶有電樞繞組。
**轉子**——它是電機的旋轉部分。同步電機的轉子產生主要的磁通。
本章將討論同步電機的定子和轉子的構造方式。
定子結構
同步電機的定子包括框架、定子鐵心、定子繞組和冷卻機構等各個部分。框架是電機的外部部分,小型電機由鑄鐵製成,大型電機由焊接鋼製成。框架包圍整個電機元件並保護其免受機械和環境影響。
定子鐵心是一個空心圓柱體,由高階矽鋼片製成。矽鋼片可減少電機的磁滯和渦流損耗。在定子鐵心的內周緣上設有許多均勻分佈的槽。三相繞組置於這些槽中。當電流流過定子繞組時,它會產生正弦磁場,從而產生電動勢。
轉子結構
在同步電機中,使用兩種型別的轉子結構,即**凸極轉子**和**圓柱形轉子**。
凸極轉子
術語**凸極**表示**突出**。因此,凸極轉子是指其磁極從轉子鐵心表面突出的轉子,如圖 2 所示。

由於轉子受到變化的磁場的作用,因此它由薄鋼片製成以減少渦流損耗。相同尺寸的磁極透過堆疊所需長度的疊片然後鉚接在一起而構成。在每個磁極鐵心周圍繞制勵磁線圈後,將磁極安裝到與轉子軸鍵合的鋼製蜘蛛上。
在每個磁極的外端,提供阻尼條以抑制負載突然變化時轉子的振盪。雖然使用凸極轉子的同步電機具有不均勻的空氣隙,其中磁極中心下的空氣隙最小,磁極之間的空氣隙最大。磁極面(磁極的外端)的形狀使得徑向空氣隙的長度從磁極中心到磁極尖端增加,因此它可以產生氣隙中正弦分佈的磁通。這將確保同步電機的平穩執行。
在凸極轉子中,各個勵磁線圈串聯連線,以便它們可以產生交替的北極和南極。勵磁線圈的兩端透過電刷和滑環連線到直流電源。
具有凸極轉子的同步電機通常具有大量的磁極,並以較低的速度執行。這些電機具有較大的直徑和較短的軸向長度。
圓柱形轉子
這種同步電機轉子結構具有光滑的圓柱形結構。對於圓柱形轉子,沒有向外突出的物理極。圓柱形轉子由高等級鎳鉻鉬鋼的整體鍛件製成。
在轉子的外圓周上,在轉子的大約三分之二處均勻地切割出槽,這些槽平行於轉子軸。勵磁繞組放置在這些槽中。勵磁繞組由直流電源供電。轉子的未開槽部分形成極面。

使用圓柱形轉子的同步電機具有較小的直徑和較長的軸向長度。圓柱形轉子結構限制了離心力的影響。因此,圓柱形轉子結構主要用於高速同步電機。此外,這種轉子結構提供了更大的機械強度,並允許對電機進行更精確的動態平衡。
使用圓柱形轉子的同步電機的主要優點是它產生的機械損耗較小。由於圓柱形轉子在電機中提供了均勻的氣隙,因此其執行噪音較小。
三相交流發電機的執行原理
三相交流發電機是一種同步電機,它透過電磁感應過程將機械能轉換為三相電能。
正如我們在前幾章中討論的那樣,三相交流發電機,也稱為三相同步發電機,具有靜止的電樞和旋轉的磁場。在三相交流發電機中,轉子繞組(充當勵磁繞組)由直流電源供電,並在轉子上產生交替的南北極。
三相交流發電機的執行
當轉子由原動機(發動機、汽輪機等)旋轉(例如逆時針方向)時,定子繞組(充當電樞繞組)被轉子極的磁通切割。由於電磁感應,在電樞繞組中感應出電動勢。這種感應電動勢是交流電,因為轉子的南北極交替地經過電樞繞組導體。我們可以用弗萊明右手定則確定感應電動勢的方向。
圖1顯示了星形連線電樞繞組和直流勵磁繞組三相交流發電機的等效電路圖。(此處應插入圖1)
當轉子旋轉時,在電樞繞組中產生三相電壓。產生的電壓大小取決於轉子旋轉速度和直流勵磁電流。然而,電樞每個相位的產生電壓大小相同,但在空間上彼此相差120°電角度,如圖所示。(此處應插入相量圖)
產生電壓的頻率
在三相交流發電機中,產生電壓的頻率取決於旋轉速度和電機中的磁極數。
設
N = 旋轉速度,單位為RPM
P = 磁極數
則產生電壓的頻率由下式給出:
$$\mathrm{\mathit{f}\:=\:\frac{\mathit{NP}}{120}\:\mathrm{Hz}\:\cdot \cdot \cdot (1)}$$
需要注意的是,N是同步速度,因為交流發電機是一種同步電機,其轉子始終以同步速度旋轉。
三相交流發電機的電動勢方程
給出三相交流發電機電樞繞組中感應電動勢值的數學關係稱為其電動勢方程。
設
N = 旋轉速度,單位為RPM
P = 轉子上的磁極數
$\phi$ = 每極磁通,單位為韋伯
Z = 每相電樞導體數
則,在一轉中,每個定子導體被$\mathit{P\phi }$ 韋伯的磁通切割,即:
$$\mathrm{\mathit{d\phi }\:=\:\mathit{P\phi }}$$
完成一轉所需的時間為:
$$\mathrm{\mathit{dt }\:=\:\frac{60}{\mathit{N}}}$$
因此,每個電樞導體中感應的平均電動勢為:
$$\mathrm{\mathrm{每導體電動勢}\:=\:\mathit{\frac{d\phi }{dt}}\:=\:\frac{\mathit{P\phi }}{(60/\mathit{N})}\:=\:\frac{\mathit{P\phi N}}{\mathrm{60}}}$$
由於Z是每相電樞繞組中的總導體數,則
$$\mathrm{\mathrm{每相平均電動勢, }\mathit{E_{av}/\mathrm{相}}\:=\:\mathit{Z\times }\frac{\mathit{P\phi N}}{\mathrm{60}}}$$
$$\mathrm{\because \mathit{N}\:=\:\frac{120\mathit{f}}{\mathit{P}}}$$
則,
$$\mathrm{\mathit{E_{av}/}\mathrm{相}\:=\:\frac{\mathit{P\phi Z}}{60}\times \frac{120\mathit{f}}{\mathit{P}}\:=\:2\mathit{f\phi Z}\:\mathrm{伏特}}$$
現在,每相產生的電動勢的有效值為:
$$\mathrm{\mathit{E_{\mathrm{RMS}}/}\mathrm{相}\:=\:\left ( \mathit{E_{av}/\mathrm{相}} \right )\times \mathrm{形狀係數}}$$
在實踐中,我們認為三相交流發電機產生正弦電壓,其形狀係數為1.11。
$$\mathrm{\mathit{E_{\mathrm{RMS}}/}\mathrm{相}\:=\:2\mathit{f\phi Z}\times 1.11}$$
$$\mathrm{\therefore \mathit{E_{\mathrm{RMS}}/}\mathrm{相}\:=\:2.22\mathit{f\phi Z}\:\mathrm{伏特}\:\cdot \cdot \cdot (2)}$$
有時,指定每相的匝數 (T) 而不是每相的導體數。在這種情況下,我們有:
$$\mathrm{\mathit{Z}\:=\:2\mathit{T}}$$
$$\mathrm{\therefore \mathit{E_{\mathrm{RMS}}/}\mathrm{相}\:=\:\mathit{E_{ph}}\:=\:4.44\mathit{f\phi T}\:\mathrm{伏特}\:\cdot \cdot \cdot (3)}$$
公式(2)和(3)中的表示式稱為三相交流發電機的電動勢方程。
數值例子(1)
具有6個磁極並以1200 RPM旋轉的三相交流發電機產生的電壓頻率是多少?
解答
已知資料:
P = 6;
N = 1200 RPM
$$\mathrm{\mathrm{頻率,}\mathit{f}\:=\:\frac{\mathit{NP}}{120}\:=\:\frac{1200\times 6}{120}}$$
$$\mathrm{\therefore\mathit{f} \:=\:60\:Hz}$$
數值例子(2)
一個4極、3相、50 Hz交流發電機的電樞有24個槽,每個槽有10個導體。一個磁極有0.03 Wb的磁通進入電樞。計算每相感應電動勢。
解答
$$\mathrm{\mathrm{總導體數}\:=\:24\times 10\:=\:240}$$
$$\mathrm{\mathrm{每相導體數,}\mathit{Z}\:=\:\frac{240}{3}\:=\:80}$$
$$\mathrm{\therefore \mathit{E_{ph}}\:=\:2.22\mathit{f\phi Z}\:=\:2.22\times 50\times 0.03\times 80}$$
$$\mathrm{\mathit{E_{ph}}\:=\:266.4\:V}$$
同步電機中的電樞反應
交流發電機的電樞反應
當三相交流發電機空載執行時,其電樞繞組中將沒有電流流過。因此,氣隙中產生的磁通僅由轉子磁極產生。但是,當交流發電機負載執行時,流過電樞繞組的三相電流將在氣隙中產生旋轉磁場。結果,氣隙中的合成磁通發生變化。這種效應稱為電樞反應,可以定義如下:
流過三相交流發電機電樞繞組的電流,產生的磁動勢(MMF)產生磁通。這種電樞磁通與主極磁通相互作用,導致氣隙中的合成磁通量小於或大於原來的主極磁通量。電樞磁通對主極磁通的影響稱為電樞反應。
在三相交流發電機中,電樞反應的影響取決於電樞電流的大小和負載的功率因數。這意味著負載的功率因數決定電樞反應磁通是否會扭曲、抵消或輔助主磁通。
以下討論解釋了同步電機在不同功率因數下的電樞反應性質:
功率因數為1 - 當交流發電機以功率因數為1的負載供電時,即純電阻負載,電樞反應的作用是扭曲主磁通。這稱為電樞反應的橫向磁化效應。
滯後功率因數 - 當交流發電機以滯後功率因數的負載供電時,即純感性負載,電樞反應的作用是部分去磁和部分橫向磁化。這會導致產生電壓降低。
超前功率因數 - 當交流發電機以超前功率因數的負載供電時,即純容性負載,電樞反應的作用是部分磁化和部分橫向磁化。這會導致產生電壓升高。
同步電動機的電樞反應
當同步電機以電動機模式執行時,電樞反應磁通處於反相,這意味著電樞反應的性質與交流發電機的相反。
以下幾點解釋了同步電機在電動機模式下執行時電樞反應的影響:
滯後功率因數 - 當同步電動機以滯後功率因數吸取電流時,電樞反應的作用是部分磁化和部分橫向磁化。
超前功率因數 - 當同步電動機以超前功率因數吸取電流時,電樞反應的作用是部分去磁和部分橫向磁化。
三相交流發電機的輸出功率
考慮一個具有圓柱形轉子的三相交流發電機,它以滯後功率因數執行。
設:
E = 每相感應電動勢
V = 每相端電壓
Ia = 每相電樞電流
cos$\phi$ = 負載的功率因數(滯後)
$\delta$ = 功率角(E和V之間的角度)
因此,三相交流發電機的輸出功率由下式給出:
$$\mathrm{\mathit{P_{0}}\:=\:3\mathit{VI_{a}cos\phi }\cdot \cdot \cdot (1)}$$
三相交流發電機的近似輸出功率
在三相交流發電機中,電樞電路的電阻$R_{a}$與電機的同步電抗$X_{s}$相比非常小。因此,我們可以忽略電樞電阻($R_{a}$),然後得到交流發電機的近似等效電路,如圖1所示。(此處應插入圖1) 電路的相量圖也如圖1所示。(此處應插入圖1)

從相量圖中,我們得到:
$$\mathrm{\mathit{AB}\:=\:\mathit{I_{a}X_{s}cos\phi }\:=\:\mathit{E}\:\mathrm{sin\delta }}$$
$$\mathrm{\Rightarrow \mathit{I_{a}cos\phi }\:=\:\frac{\mathit{E\:\mathrm{sin\delta }}}{\mathit{X_{s}}}\cdot \cdot \cdot (2)}$$
現在,從公式(1)和(2),我們得到:
$$\mathrm{\mathit{P_{0}}\:=\:\frac{3\mathit{EV\:\mathrm{sin\delta }}}{\mathit{X_{s}}}\cdot \cdot \cdot (3)}$$
公式3中的表示式給出了三相交流發電機的近似輸出功率。
當交流發電機以恆定速度和恆定的勵磁電流執行時,Xs和E都是恆定的,因此端電壓V也是恆定的。因此,從公式3可以看出:
$$\mathrm{\mathit{P_{0}}\propto \:\mathrm{sin\delta }}$$
我們知道,當$\delta$ = 90°時,則
$$\mathrm{\mathrm{sin\:90^{\circ}}\:=\:1}$$
因此,交流發電機在$$ =90°時提供最大功率,由下式給出:
$$\mathrm{\mathit{P_{max}}\:=\:\frac{3\mathit{EV}}{\mathit{X_{s}}}}\cdot \cdot \cdot (4)$$
公式4給出的最大功率稱為交流發電機的靜態穩定極限。
數值例子
一臺三相、11 kV、3 MVA星形連線交流發電機每相同步電抗為10 $\Omega$。其勵磁使得產生的線電壓為15 kV。當交流發電機連線到無限大母線時。忽略電樞電阻,計算該勵磁下交流發電機的最大輸出功率。
解答
已知資料:
$$\mathrm{\mathrm{線電壓,}\mathit{V_{L}}\:=\:11\:kV\:=\:11000\:V}$$
$$\mathrm{\therefore\:\mathrm{每相端電壓,}\mathit{V}\:=\:\frac{11000}{\sqrt{3}}\:=\:6350.85\:V}$$
$$\mathrm{\mathrm{產生的線電壓}\:=\:15\:kV\:=\:15000\:V}$$
$$\mathrm{\therefore\:\mathrm{每相產生的電動勢,}\mathit{E}\:=\:\frac{15000}{\sqrt{3}}\:=\:8660.25\:V}$$
$$\mathrm{\mathrm{每相同步電抗,}\:\mathit{X_{s}}\:=\:10\:\Omega }$$
因此,交流發電機的最大輸出功率將為:
$$\mathrm{\mathit{P_{max}}\:=\:\frac{3\mathit{EV}}{\mathit{X_{s}}}\:=\:\frac{3\times 8660.25\times 6350.85}{10}}$$
$$\mathrm{\therefore \mathit{P_{max}}\:=\:16499\times 10^{3}W\:=\:16499\:\mathrm{kW}}$$
三相交流發電機的損耗和效率
三相交流發電機的損耗
三相交流發電機中發生的損耗可以分為以下四類:
銅損
鐵損或鐵芯損耗
機械損耗
雜散負載損耗
通讀本節,瞭解三相交流發電機中發生的各種損耗型別。
銅損
銅損發生在交流發電機的電樞繞組和轉子繞組中,這是由於當電流流過它們時,它們的電阻造成的。因此,這些損耗也稱為I2R損耗。
鐵損或鐵芯損耗
鐵損或鐵芯損耗發生在交流發電機的鐵部件(如定子鐵芯和轉子鐵芯)中。這些損耗包括磁滯損耗和渦流損耗。鐵芯損耗的產生是因為交流發電機的各種鐵部件都受到變化的磁場的影響。
機械損耗
交流發電機的機械損耗發生在轉動部件中,例如轉子、軸、軸承等。機械損耗主要分為兩種:摩擦損耗和風損。摩擦損耗是由於發電機軸承的摩擦造成的,而風損是由於發電機的旋轉部件與發電機外殼內的空氣之間的摩擦造成的。
附加負載損耗
此類損耗難以精確計算,也稱為雜散損耗。附加負載損耗可能由以下原因引起:
電樞反應導致主磁通畸變。
電樞導體橫截面上的電流分佈不均勻。
在實際計算中,我們將附加負載損耗取為滿載損耗的1%。
注意
鐵損和機械損耗合稱為旋轉損耗,因為這些損耗是由於轉子旋轉而產生的。
發電機中發生的這些損耗都會轉化為熱量,導致溫度升高和效率降低。
三相交流發電機效率
發電機的輸出功率與輸入功率之比稱為發電機效率。效率通常以百分比表示。
$\mathrm{\mathrm{效率,} \: \eta \:=\:\frac{輸出功率}{輸入功率}\times 100\%\:=\:\frac{輸出功率}{輸出功率+損耗}\times 100\%}$
現在,我們將推導三相交流發電機效率的表示式。為此,考慮一個在滯後功率因數下執行的三相交流發電機。
設:
V= 每相端電壓
Ia = 每相電樞電流
cos $\phi$ = 負載功率因數(滯後)
因此,三相交流發電機的輸出功率由下式給出:
$$\mathrm{\mathit{P_{0}}\:=\:3\:\mathit{VI_{a}cos\:\phi }}$$
發電機的損耗為:
$$\mathrm{\mathrm{電樞銅損,}\mathit{P_{cu}}\:=\:3\:\mathit{I_{\mathit{a}}^{\mathrm{2}}R_{a}}}$$
$$\mathrm{\mathrm{勵磁繞組銅損}\:=\:\mathit{V_{f}I_{f}}}$$
其中,Vf是勵磁繞組上的直流電壓,If是直流勵磁電流。
$$\mathrm{\mathrm{旋轉損耗,}\mathit{P_{r}}\:=\:\mathrm{鐵損\:+\:機械損耗}}$$
$$\mathrm{\mathrm{附加負載損耗}\mathit{P_{s}}}$$
$$\mathrm{\therefore \mathrm{發電機總損耗,}\mathit{P_{loss}}\:=\:3\:\mathit{I_{a}^{2}R_{a}\:+\:P_{r}\:+\:P_{s}\:+\:V_{f}I_{f}}}$$
由於轉子旋轉速度恆定,因此旋轉損耗恆定。勵磁繞組銅損也恆定。如果我們假設附加負載損耗為恆定值,則有:
$$\mathrm{\mathrm{總恆定損耗,}\mathit{P_{c}}\:=\:\mathit{P_{r}\:+\:P_{s}\:+\:V_{f}I_{f}}}$$
$$\mathrm{\therefore\:\mathrm{可變損耗} \:=\:\mathrm{3}\mathit{I_{a}^{\mathrm{2}}R_{a}}}$$
因此,發電機效率由下式給出:
$$\mathrm{\eta \:=\:\frac{\mathit{P_{0}}}{\mathit{P_{0}+\mathrm{損耗}}}\:=\:\frac{3\mathit{VI_{a}cos\phi }}{3\mathit{VI_{a}cos\phi \:+\:\mathrm{3}\mathit{I_{a}^{\mathrm{2}}R_{a}}\:+P_{c}}}\cdot \cdot \cdot (1)}$$
公式(1)可用於確定三相交流發電機的效率。
最大效率的條件
當可變損耗等於恆定損耗時,發電機效率最高,即:
$$\mathrm{\mathit{P_{c}}\:=\:3\:\mathit{I_{a}^{\mathrm{2}}R_{a}}\cdot \cdot \cdot (2)}$$
實際上,交流發電機的最大效率通常出現在額定滿載的85%左右。
數值例子
一臺三相交流發電機每相端電壓為230 V,每相電樞電流為14.4 A。發電機電樞電路電阻為0.5Ω,恆定損耗為200瓦。如果它以0.8滯後功率因數供電,計算發電機的效率和最大效率。
解答
$$\mathrm{\mathrm{效率,}\eta \:=\:\frac{3\mathit{VI_{a}cos\phi }}{3\mathit{VI_{a}cos\phi \:+\:\mathrm{3}\mathit{I_{a}^{\mathrm{2}}R_{a}}\:+P_{c}}}}$$
$$\mathrm{\Rightarrow\:\eta \:=\:\frac{3\times 230\times 14.4\times 0.8}{\left ( 3\times 230\times 14.4\times 0.8 \right )\:+\:\left ( 3\times 14.4^{2}\times 0.5 \right )\:+\:200}}$$
$$\mathrm{\therefore \eta \:=\:0.9395\:=\:93.95\%}$$
對於發電機的最大效率,
$$\mathrm{\mathit{P_{c}}\:=\:3\:\mathit{I_{a}^{\mathrm{2}}R_{a}}}$$
$$\mathrm{\therefore \eta_{max} \:=\:\frac{3\mathit{VI_{a}cos\phi }}{3\mathit{VI_{a}cos\phi \:+\:\mathrm{2}\mathit{P_{c}}}}\:=\:\frac{3\times 230\times 14.4\times 0.8}{\left ( 3\times 230\times 14.4\times 0.8 \right )\:+\:\left (2\times 200 \right )}}$$
$$\mathrm{\therefore \eta_{max} \:=\:0.9521\:=\:95.21\%}$$
三相同步電機的執行原理
將三相電能轉換為機械能的三相同步電機稱為三相同步電動機。
三相同步電動機是恆速電機,它以同步速度執行。三相同步電動機的同步速度由下式給出:
$$ \mathrm{\mathit{N_{s}}\:=\:\frac{120\mathit{f}}{\mathit{p}}\cdot \cdot \cdot (1)} $$
其中,f是電源頻率,P是電機中的磁極對數。
與任何其他電動機一樣,三相同步電動機也由兩個主要部分組成,即定子和轉子。定子裝有三相電樞繞組,並從三相交流電源接收電力。轉子是旋轉部件,帶有勵磁繞組,勵磁繞組由外部直流電源激勵。
同步電動機的最主要缺點是它不能自啟動,因此必須使用輔助手段啟動它。
三相同步電機的執行原理
考慮一個具有凸極式轉子的三相同步電動機,該轉子有兩個磁極,分別為$\mathit{N_{\mathrm{2}}}$和$\mathit{S_{\mathrm{2}}}$。因此,定子也將繞製成兩個磁極,分別為$\mathit{N_{\mathrm{1}}}$和$\mathit{S_{\mathrm{1}}}$。直流電壓施加到轉子繞組,平衡的三相交流電壓施加到定子繞組。
定子繞組產生一個旋轉磁場,該磁場以同步速度($\mathit{N_{\mathit{s}}}$)圍繞定子旋轉。流過轉子繞組的直流電流在轉子中產生兩個磁極,只要轉子不轉動,這兩個磁極產生的磁場就是靜止的。因此,在這種情況下,我們有一對旋轉的電樞磁極 ($\left ( \mathit{N_{\mathrm{1}}}-\mathit{S_{\mathrm{1}}} \right )$)和一對靜止的轉子磁極 ($\left ( \mathit{N_{\mathrm{2}}}-\mathit{S_{\mathrm{2}}} \right )$)。
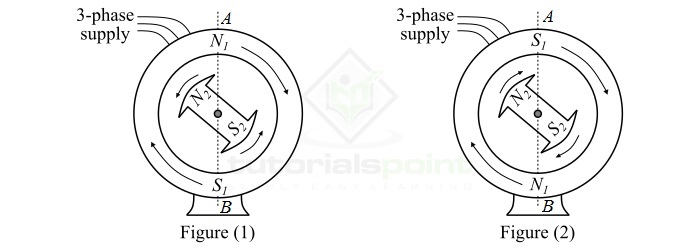
現在,考慮定子磁極位於A和B位置的瞬間,如圖1所示。很明顯,磁極$\mathit{N_{\mathrm{1}}}$和$\mathit{N_{\mathrm{2}}}$互相排斥,磁極$\mathit{S_{\mathrm{1}}}$和$\mathit{S_{\mathrm{1}}}$也是如此。因此,轉子傾向於逆時針旋轉。在交流電源半個週期後,定子磁極的極性反轉,但轉子磁極的極性保持不變,如圖2所示。在這種情況下,磁極$\mathit{S_{\mathrm{1}}}$和$\mathit{N_{\mathrm{2}}}$互相吸引,磁極$\mathit{N_{\mathrm{1}}}$和$\mathit{S_{\mathrm{2}}}$也是如此。因此,轉子現在傾向於順時針旋轉。
由於定子磁極迅速改變極性,它們傾向於先在一個方向上拉動轉子,然後在交流電半個週期後在另一個方向上拉動轉子。由於轉子上的雙向轉矩和轉子的高慣性,同步電動機無法啟動。因此,同步電動機沒有自啟動轉矩。
使同步電動機自啟動
同步電動機不能自行啟動。為了使電動機能夠自啟動,在轉子上設定了一個鼠籠式繞組,稱為阻尼繞組。阻尼繞組由嵌入轉子凸極極靴槽中的銅條組成,如圖3所示。
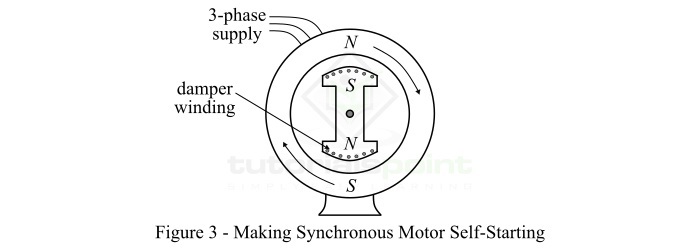
這些阻尼繞組用於使同步電動機自行啟動,解釋如下:
最初,三相電源供電給定子繞組,而轉子繞組保持斷開狀態。定子繞組的旋轉磁場在阻尼繞組中感應出電流,由於電磁力,轉子開始運動。因此,同步電動機作為非同步電動機啟動。
一旦電動機達到接近同步速度的速度,轉子繞組就會從直流電源勵磁。現在,轉子上的磁極面對極性相反的定子磁極,並在它們之間建立強大的磁吸引力。因此,轉子磁極與定子的旋轉磁極鎖定。因此,轉子以與定子磁極相同的速度旋轉,即同步速度。
由於轉子現在以與定子磁場相同的速度旋轉,阻尼條不切割任何磁通,因此在其中沒有感應電流。因此,轉子的阻尼繞組實際上從電動機的執行中移除。
透過這種方式,同步電動機可以自啟動。必須注意的是,由於定子和轉子磁極之間的磁互鎖,同步電動機只能以同步速度執行。
同步電機的等效電路和功率因數
同步電動機的等效電路
同步電動機是一個雙激系統,這意味著它連線到兩個電力系統,其中三相交流電源連線到電樞繞組,直流電源連線到轉子繞組。圖1顯示了三相同步電動機的每相等效電路。

這裡,V是施加到電機的每相電壓,Ra是每相電樞電阻,$X_{s}$是每相同步電抗。這兩個引數(即$R_{a}$和$X_{s}$)給出電機的每相同步阻抗($Z_{s}$)。
從同步電動機的等效電路(如圖1所示)中,我們可以寫出它的電壓方程為:
$$\mathrm{\mathit{V}\:=\:\mathit{E_{b}+I_{a}Z_{s}}}$$
$$\mathrm{\Rightarrow \mathit{V}\:=\:\mathit{E_{b}+I_{a}\left ( R_{a} +jX_{s}\right )}}$$
其中,粗體字母表示相量。
因此,每相電樞電流由下式給出
$$\mathrm{I_{a}\:=\:\frac{\mathit{V-E_{b}}}{\mathit{Z_{s}}}\:=\:\frac{\mathit{V-E_{b}}}{\left ( \mathit{R_{a}+jX_{s}}\right )}\:=\:\frac{\mathit{E_{r}}}{\mathit{R_{a}+jX_{s}}}}$$
其中,$\mathit{E_{r}}$是電樞電路中的合成電壓。
同步電動機的電樞電流和同步阻抗是具有幅值和相角的相量。因此,電樞電流的幅值由下式給出:
$$\mathrm{\left|I_{a} \right|\:=\:\frac{\mathit{V-E_{b}}}{\mathit{Z_{s}}}\:=\:\frac{\mathit{E_{r}}}{\mathit{Z_{s}}}}$$
同步阻抗的幅值由下式給出:
$$\mathrm{\left|Z_{s} \right|\:=\:\sqrt{\mathit{R_{a}^{\mathrm{2}}+X_{s}^{\mathrm{2}}}}}$$
等效電路和上述方程有助於理解同步電動機的執行,如:
當勵磁電流使得$\mathit{E_{b}=V}$時,則稱同步電動機為正常勵磁。
當勵磁電流使得$\mathit{E_{b}<V}$時,則稱同步電動機為欠勵磁。
當勵磁電流使得$\mathit{E_{b}> V}$時,則稱同步電動機為過勵磁。
正如我們將在下一節中看到的,同步電動機的勵磁會影響其功率因數。
同步電動機的功率因數
同步電動機的最重要的特性之一是,可以透過改變勵磁來使其在超前、滯後或單位功率因數下執行。以下討論解釋了勵磁變化如何影響同步電動機的功率因數:
當轉子勵磁電流足以產生所有所需的磁通量時,則機器不需要額外的無功功率。因此,電動機將在單位功率因數下執行。
當轉子勵磁電流小於所需電流時,即電動機欠勵磁。在這種情況下,電動機將從電源吸收無功功率以提供剩餘的磁通量。因此,電動機將在滯後功率因數下執行。
當轉子勵磁電流超過所需電流時,即電機過勵磁。在這種情況下,電機將向三相線路提供無功功率,並表現為無功功率源。因此,電機將在**超前功率因數**下執行。
因此,我們可以得出結論:**同步電機欠勵磁時吸收無功功率,過勵磁時發出無功功率。**
同步電機產生的功率
本章將推導三相同步電機**輸出機械功率**(Pm)的表示式。這裡,我們將忽略同步電機的電樞電阻Ra。則電樞銅損將為零,因此電機輸出的機械功率等於電機的輸入功率(Pin),即:
$$\mathrm{\mathit{P_{m}}\:=\:\mathit{P_{in}}}$$
現在,考慮一個欠勵磁(即,Eb<V)的三相同步電機,其電樞電阻為零(即,Ra = 0),並且正在驅動機械負載。

該同步電機一相的相量圖如圖所示。由於電機欠勵磁,因此它將在滯後功率因數下執行,例如(cos $\phi$)。從相量圖可以看出,$\mathit{E_{r}}\:=\:I_{a}X_{s}$,並且每相電樞電流$I_{a}$滯後於合成電動勢$\mathit{E_{r}}$ 90°。
因此,電機的每相輸入功率由下式給出:
$$\mathrm{\mathit{P_{in}}\:=\mathit{VI_{a}}\:cos\:\phi \:\cdot \cdot \cdot (1)}$$
由於$\mathit{P_{m}}$等於$\mathit{P_{in}}$,因此:
$$\mathrm{\mathit{P_{m}}\:=\mathit{VI_{a}}\:cos\:\phi \:\cdot \cdot \cdot (2)}$$
從相量圖中,我們有:
$$\mathrm{\mathit{AB}\:=\mathit{I_{a}X_{s}}\:cos\:\phi \:=\:\mathit{E}_{\mathit{b}}\:sin\:\delta}$$
$$\mathrm{\therefore \mathit{I_{a}\:cos\phi \:=\:\frac{E_{b}\:sin\delta }{\mathit{X_{s}}}}\:\cdot \cdot \cdot (3)}$$
利用公式(2)和(3),我們得到:
$$\mathit{P_{m}\:=\:\frac{\mathit{VE_{b}}sin\delta }{X_{s}}}\cdot \cdot \cdot (4)$$
這是同步電機每相輸出機械功率(Pm)的表示式。
對於電機的三相,輸出的機械功率由下式給出:
$$\mathit{P_{m}\:=\:\frac{3\mathit{VE_{b}}sin\delta }{X_{s}}}\cdot \cdot \cdot (5)$$
此外,從公式(4)和(5)可以看出,當功率角($\delta$= 90°)(電角度)時,輸出的機械功率最大。因此:
每相:
$$\mathit{P_{max}\:=\:\frac{\mathit{VE_{b}}}{X_{s}}}\cdot \cdot \cdot (6)$$
三相:
$$\mathit{P_{max}\:=\:\frac{\mathit{3VE_{b}}}{X_{s}}}\cdot \cdot \cdot (7)$$
要點
關於三相同步電機輸出的機械功率,需要注意以下幾點:
同步電機輸出的機械功率隨著功率角($\delta$)的增加而增加,反之亦然。
如果功率角($\delta$)為零,則同步電機無法產生機械功率。
當同步電機的勵磁被減小到零時,即($E_{b}$ = 0),電機輸出的機械功率也為零,即電機將停止執行。
數值例子
一臺三相4000 kW,3.3 kV,200 RPM,50 Hz的同步電機,每相同步電抗為1.5 $\Omega$。滿載時,功率角為22°(電角度)。如果每相產生的反電動勢為1.7 kV,計算輸出的機械功率。最大機械功率是多少?
解答
已知資料:
每相電壓,$\mathit{V}\:=\:\frac{3.3}{\sqrt{3}}\:=\:1.9\:kV$
每相反電動勢,$\mathit{E_{b}}\:=\:1.7\:kV$
同步電抗,$X_{s}\:=\:1.5\Omega $
功率角,$\delta \:=\:22^{^{\circ}}$
因此,電機輸出的機械功率為:
$$\mathrm{\mathit{P_{m}}\:=\:\frac{3\:\mathit{VE_{b}\:sin\delta} }{\mathit{X_{s}}}\:=\:\frac{3\times 1.9\times 1.7\times \mathrm{sin}\:22^{\circ}}{1.5}}$$
$$\mathit{\therefore P_{m}}\:=\:2.42\times 10^{6}\:W\:=\:2.42\:MW$$
當($\delta$ =90°)時,輸出的機械功率最大:
$$\mathit{P_{max}}\:=\:\frac{3\mathit{VE_{b}}}{X_{s}}\:=\:\frac{3\times 1.9\times 1.7}{1.5}$$
$$\mathit{\therefore P_{max}}\:=\:6.46\:\mathrm{MW}$$