
- 凸最佳化教程
- 首頁
- 簡介
- 線性規劃
- 範數
- 內積
- 極小值和極大值
- 凸集
- 仿射集
- 凸包
- Caratheodory定理
- Weierstrass定理
- 最近點定理
- 基本分離定理
- 凸錐
- 極錐
- 錐組合
- 多面體集
- 凸集的極點
- 方向
- 凸函式和凹函式
- Jensen不等式
- 可微凸函式
- 全域性最優的充分必要條件
- 擬凸函式和擬凹函式
- 可微擬凸函式
- 嚴格擬凸函式
- 強擬凸函式
- 偽凸函式
- 凸規劃問題
- Fritz-John條件
- Karush-Kuhn-Tucker最優性必要條件
- 凸問題演算法
- 凸最佳化資源
- 凸最佳化 - 快速指南
- 凸最佳化 - 資源
- 凸最佳化 - 討論
凸最佳化 - 快速指南
凸最佳化 - 簡介
本課程適用於希望解決各種工程和科學應用中出現的非線性最佳化問題的學生。本課程從線性規劃的基本理論開始,將介紹凸集和凸函式的概念以及相關術語,以解釋解決非線性規劃問題所需的各種定理。本課程將介紹用於解決此類問題的各種演算法。這些型別的問題出現在各種應用中,包括機器學習、電氣工程中的最佳化問題等。它要求學生具備高中數學概念和微積分的預備知識。
在本課程中,學生將學習如何解決諸如 $min f\left ( x \right )$ 受某些約束條件的最佳化問題。
如果函式 $f\left ( x \right )$ 是線性函式,並且約束條件是線性的,則這些問題很容易解決。然後它被稱為線性規劃問題 (LPP)。但是,如果約束條件是非線性的,則很難解決上述問題。除非我們可以在圖上繪製函式,然後嘗試分析最佳化可能是一種方法,但如果函式超過三維,我們就無法繪製它。因此,出現了非線性規劃或凸規劃的技術來解決此類問題。在本教程中,我們將重點學習這些技術,最後介紹一些解決此類問題的演算法。首先,我們將引入凸集的概念,它是凸規劃問題的基礎。然後,隨著凸函式的引入,我們將介紹一些重要的定理來解決這些問題,以及基於這些定理的一些演算法。
術語
空間 $\mathbb{R}^n$ - 它是一個具有實數的n維向量,定義如下 - $\mathbb{R}^n=\left \{ \left ( x_1,x_2,...,x_n \right )^{\tau }:x_1,x_2,....,x_n \in \mathbb{R} \right \}$
空間 $\mathbb{R}^{mXn}$ - 它是一組所有階為 $mXn$ 的實值矩陣。
凸最佳化 - 線性規劃
方法
線性規劃也稱為線性最佳化,是一種用於解決數學問題的技術,其中關係本質上是線性的。線性規劃的基本性質是最大化或最小化目標函式,同時受某些約束條件的限制。目標函式是一個線性函式,它是從問題的數學模型中獲得的。約束條件是強加於模型上的條件,並且也是線性的。
- 根據給定的問題,找到目標函式。
- 找到約束條件。
- 在圖上繪製約束條件。
- 找到可行域,它是由所有約束條件的交集形成的。
- 找到可行域的頂點。
- 找到目標函式在這些頂點處的取值。
- 使目標函式最大化或最小化(根據問題)的頂點就是答案。
示例
步驟 1 - 最大化 $5x+3y$,受以下條件限制
$x+y\leq 2$,
$3x+y\leq 3$,
$x\geq 0 \:and \:y\geq 0$
解答 -
第一步是在圖上找到可行域。
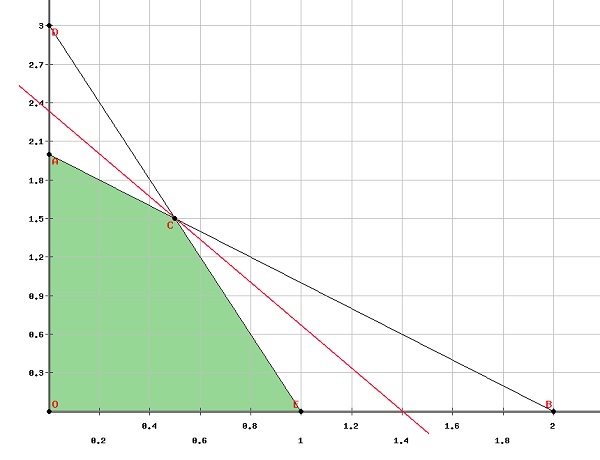
從圖中可以清楚地看出,可行域的頂點是
$\left ( 0, 0 \right )\left ( 0, 2 \right )\left ( 1, 0 \right )\left ( \frac{1}{2}, \frac{3}{2} \right )$
令 $f\left ( x, y \right )=5x+3y$
將這些值代入目標函式,我們得到 -
$f\left ( 0, 0 \right )$=0
$f\left ( 0, 2 \right )$=6
$f\left ( 1, 0 \right )$=5
$f\left ( \frac{1}{2}, \frac{3}{2} \right )$=7
因此,函式在 $\left ( \frac{1}{2}, \frac{3}{2} \right )$ 處取得最大值。
步驟 2 - 一家手錶公司生產電子錶和機械錶。長期預測表明,每天預計至少需要 100 塊電子錶和 80 塊機械錶。由於生產能力的限制,每天最多隻能生產 200 塊電子錶和 170 塊機械錶。為了滿足運輸合同,每天必須運送至少 200 塊手錶。
如果每售出一塊電子錶就會造成 2 美元的損失,但每售出一塊機械錶就會產生 5 美元的利潤,那麼每天應該生產多少塊每種型別的手錶才能使淨利潤最大化?
解答 -
設 $x$ 為生產的電子錶數量
$y$ 為生產的機械錶數量
根據問題,每天至少要生產 100 塊電子錶,最多可以生產 200 塊電子錶。
$\Rightarrow 100 \leq \:x\leq 200$
同樣,每天至少要生產 80 塊機械錶,最多可以生產 170 塊機械錶。
$\Rightarrow 80 \leq \:y\leq 170$
由於每天至少要生產 200 塊手錶。
$\Rightarrow x +y\leq 200$
由於每售出一塊電子錶就會造成 2 美元的損失,但每售出一塊機械錶就會產生 5 美元的利潤,
總利潤可以計算為
$利潤 =-2x + 5y$
並且我們必須使利潤最大化,因此,問題可以表述為 -
最大化 $-2x + 5y$,受以下條件限制
$100 \:\leq x\:\leq 200$
$80 \:\leq y\:\leq 170$
$x+y\:\leq 200$
將上述方程在圖上繪製,我們得到,
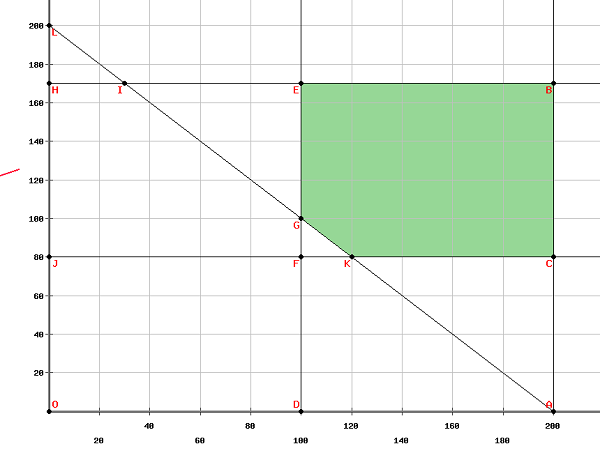
可行域的頂點是
$\left ( 100, 170\right )\left ( 200, 170\right )\left ( 200, 180\right )\left ( 120, 80\right ) and \left ( 100, 100\right )$
目標函式的最大值在 $\left ( 100, 170\right )$ 處獲得。因此,為了使淨利潤最大化,應該生產 100 個電子錶和 170 個機械錶。
凸最佳化 - 範數
範數是一個函式,它為向量或變數賦予嚴格的正值。
範數是一個函式 $f:\mathbb{R}^n\rightarrow \mathbb{R}$
範數的基本特徵是 -
設 $X$ 為一個向量,使得 $X\in \mathbb{R}^n$
$\left \| x \right \|\geq 0$
$\left \| x \right \|= 0 \Leftrightarrow x= 0\forall x \in X$
$\left \|\alpha x \right \|=\left | \alpha \right |\left \| x \right \|\forall \:x \in X and \:\alpha \:is \:a \:scalar$
$\left \| x+y \right \|\leq \left \| x \right \|+\left \| y \right \| \forall x,y \in X$
$\left \| x-y \right \|\geq \left \| \left \| x \right \|-\left \| y \right \| \right \|$
根據定義,範數計算如下 -
$\left \| x \right \|_1=\displaystyle\sum\limits_{i=1}^n\left | x_i \right |$
$\left \| x \right \|_2=\left ( \displaystyle\sum\limits_{i=1}^n\left | x_i \right |^2 \right )^{\frac{1}{2}}$
$\left \| x \right \|_p=\left ( \displaystyle\sum\limits_{i=1}^n\left | x_i \right |^p \right )^{\frac{1}{p}},1 \leq p \leq \infty$
範數是一個連續函式。
證明
根據定義,如果 $x_n\rightarrow x$ in $X\Rightarrow f\left ( x_n \right )\rightarrow f\left ( x \right ) $ 則 $f\left ( x \right )$ 是一個常數函式。
令 $f\left ( x \right )=\left \| x \right \|$
因此,$\left | f\left ( x_n \right )-f\left ( x \right ) \right |=\left | \left \| x_n \right \| -\left \| x \right \|\right |\leq \left | \left | x_n-x \right | \:\right |$
由於 $x_n \rightarrow x$,因此 $\left \| x_n-x \right \|\rightarrow 0$
因此 $\left | f\left ( x_n \right )-f\left ( x \right ) \right |\leq 0\Rightarrow \left | f\left ( x_n \right )-f\left ( x \right ) \right |=0\Rightarrow f\left ( x_n \right )\rightarrow f\left ( x \right )$
因此,範數是一個連續函式。
凸最佳化 - 內積
內積是一個函式,它為一對向量賦予一個標量。
內積 - $f:\mathbb{R}^n \times \mathbb{R}^n\rightarrow \kappa$,其中 $\kappa$ 是一個標量。
內積的基本特徵如下 -
設 $X \in \mathbb{R}^n$
$\left \langle x,x \right \rangle\geq 0, \forall x \in X$
$\left \langle x,x \right \rangle=0\Leftrightarrow x=0, \forall x \in X$
$\left \langle \alpha x,y \right \rangle=\alpha \left \langle x,y \right \rangle,\forall \alpha \in \kappa \: and\: \forall x,y \in X$
$\left \langle x+y,z \right \rangle =\left \langle x,z \right \rangle +\left \langle y,z \right \rangle, \forall x,y,z \in X$
$\left \langle \overline{y,x} \right \rangle=\left ( x,y \right ), \forall x, y \in X$
注意 -
範數和內積之間的關係:$\left \| x \right \|=\sqrt{\left ( x,x \right )}$
$\forall x,y \in \mathbb{R}^n,\left \langle x,y \right \rangle=x_1y_1+x_2y_2+...+x_ny_n$
示例
1. 找到 $x=\left ( 1,2,1 \right )\: and \: y=\left ( 3,-1,3 \right )$ 的內積。
解答
$\left \langle x,y \right \rangle =x_1y_1+x_2y_2+x_3y_3$
$\left \langle x,y \right \rangle=\left ( 1\times3 \right )+\left ( 2\times-1 \right )+\left ( 1\times3 \right )$
$\left \langle x,y \right \rangle=3+\left ( -2 \right )+3$
$\left \langle x,y \right \rangle=4$
2. 若 $x=\left ( 4,9,1 \right ),y=\left ( -3,5,1 \right )$ 且 $z=\left ( 2,4,1 \right )$,求 $\left ( x+y,z \right )$
解答
我們知道,$\left \langle x+y,z \right \rangle=\left \langle x,z \right \rangle+\left \langle y,z \right \rangle$
$\left \langle x+y,z \right \rangle=\left ( x_1z_1+x_2z_2+x_3z_3 \right )+\left ( y_1z_1+y_2z_2+y_3z_3 \right )$
$\left \langle x+y,z \right \rangle=\left \{ \left ( 4\times 2 \right )+\left ( 9\times 4 \right )+\left ( 1\times1 \right ) \right \}+$
$\left \{ \left ( -3\times2 \right )+\left ( 5\times4 \right )+\left ( 1\times 1\right ) \right \}$
$\left \langle x+y,z \right \rangle=\left ( 8+36+1 \right )+\left ( -6+20+1 \right )$
$\left \langle x+y,z \right \rangle=45+15$
$\left \langle x+y,z \right \rangle=60$
凸最佳化 - 極小值和極大值
區域性極小值或極小點
$\bar{x}\in \:S$ 被稱為函式 $f$ 的區域性極小值,如果 $f\left ( \bar{x} \right )\leq f\left ( x \right ),\forall x \in N_\varepsilon \left ( \bar{x} \right )$,其中 $N_\varepsilon \left ( \bar{x} \right )$ 表示 $\bar{x}$ 的鄰域,即 $N_\varepsilon \left ( \bar{x} \right )$ 表示 $\left \| x-\bar{x} \right \|< \varepsilon$
區域性極大值或極大點
$\bar{x}\in \:S$ 被稱為函式 $f$ 的區域性極大值,如果 $f\left ( \bar{x} \right )\geq f\left ( x \right ), \forall x \in N_\varepsilon \left ( \bar{x} \right )$,其中 $N_\varepsilon \left ( \bar{x} \right )$ 表示 $\bar{x}$ 的鄰域,即 $N_\varepsilon \left ( \bar{x} \right )$ 表示 $\left \| x-\bar{x} \right \|< \varepsilon$
全域性極小值
$\bar{x}\in \:S$ 被稱為函式 $f$ 的全域性極小值,如果 $f\left ( \bar{x} \right )\leq f\left ( x \right ), \forall x \in S$
全域性極大值
$\bar{x}\in \:S$ 被稱為函式 $f$ 的全域性極大值,如果 $f\left ( \bar{x} \right )\geq f\left ( x \right ), \forall x \in S$
示例
步驟 1 - 求 $f\left ( \bar{x} \right )=\left | x^2-4 \right |$ 的區域性極小值和極大值
解答 -
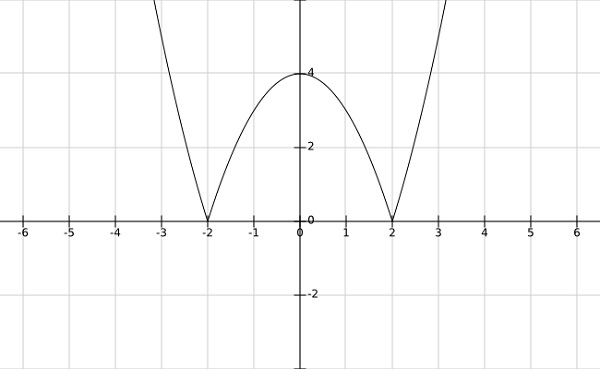
從上述函式的影像可以看出,區域性極小值出現在 $x= \pm 2$ 處,區域性極大值出現在 $x = 0$ 處。
步驟 2 - 求函式 $f\left (x \right )=\left | 4x^3-3x^2+7 \right |$ 的全域性極小值
解答 -
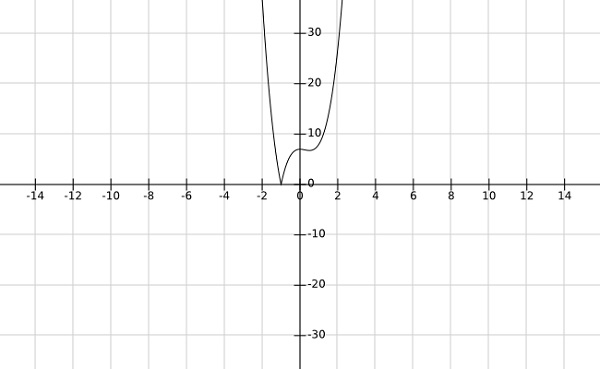
從上述函式的影像可以看出,全域性極小值出現在 $x=-1$ 處。
凸最佳化 - 凸集
設 $S\subseteq \mathbb{R}^n$,如果集合 S 中任意兩點的連線段也屬於 S,則稱集合 S 為凸集,即如果 $x_1,x_2 \in S$,則 $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S$,其中 $\lambda \in\left ( 0,1 \right )$。
注意 -
- 兩個凸集的並集可能是凸集也可能不是凸集。
- 兩個凸集的交集總是凸集。
證明
設 $S_1$ 和 $S_2$ 為兩個凸集。
設 $S_3=S_1 \cap S_2$
設 $x_1,x_2 \in S_3$
由於 $S_3=S_1 \cap S_2$,因此 $x_1,x_2 \in S_1$ 且 $x_1,x_2 \in S_2$
由於 $S_i$ 是凸集,$\forall$ $i \in 1,2,$
因此 $\lambda x_1+\left ( 1-\lambda \right )x_2 \in S_i$,其中 $\lambda \in \left ( 0,1 \right )$
所以,$\lambda x_1+\left ( 1-\lambda \right )x_2 \in S_1\cap S_2$
$\Rightarrow \lambda x_1+\left ( 1-\lambda \right )x_2 \in S_3$
因此,$S_3$ 是一個凸集。
形式為 $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$ 的加權平均,其中 $\displaystyle\sum\limits_{i=1}^k \lambda_i=1$ 且 $\lambda_i\geq 0,\forall i \in \left [ 1,k \right ]$,稱為 $x_1,x_2,....x_k$ 的錐組合。
形式為 $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$ 的加權平均,其中 $\displaystyle\sum\limits_{i=1}^k \lambda_i=1$,稱為 $x_1,x_2,....x_k$ 的仿射組合。
形式為 $\displaystyle\sum\limits_{i=1}^k \lambda_ix_i$ 的加權平均,稱為 $x_1,x_2,....x_k$ 的線性組合。
示例
步驟 1 - 證明集合 $S=\left \{ x \in \mathbb{R}^n:Cx\leq \alpha \right \}$ 是一個凸集。
解答
設 $x_1$ 和 $x_2 \in S$
$\Rightarrow Cx_1\leq \alpha$ 且 $\:Cx_2\leq \alpha$
要證明:$\:\:y=\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\in S \:\forall \:\lambda \in\left ( 0,1 \right )$
$Cy=C\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )=\lambda Cx_1+\left ( 1-\lambda \right )Cx_2$
$\Rightarrow Cy\leq \lambda \alpha+\left ( 1-\lambda \right )\alpha$
$\Rightarrow Cy\leq \alpha$
$\Rightarrow y\in S$
因此,$S$ 是一個凸集。
步驟 2 - 證明集合 $S=\left \{ \left ( x_1,x_2 \right )\in \mathbb{R}^2:x_{1}^{2}\leq 8x_2 \right \}$ 是一個凸集。
解答
設 $x,y \in S$
設 $x=\left ( x_1,x_2 \right )$ 且 $y=\left ( y_1,y_2 \right )$
$\Rightarrow x_{1}^{2}\leq 8x_2$ 且 $y_{1}^{2}\leq 8y_2$
要證明 - $\lambda x+\left ( 1-\lambda \right )y\in S\Rightarrow \lambda \left ( x_1,x_2 \right )+\left (1-\lambda \right )\left ( y_1,y_2 \right ) \in S\Rightarrow \left [ \lambda x_1+\left ( 1- \lambda)y_2] \in S\right ) \right ]$
$現在, \left [\lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}=\lambda ^2x_{1}^{2}+\left ( 1-\lambda \right )^2y_{1}^{2}+2 \lambda\left ( 1-\lambda \right )x_1y_1$
但是 $2x_1y_1\leq x_{1}^{2}+y_{1}^{2}$
因此,
$\left [ \lambda x_1 +\left ( 1-\lambda \right )y_1\right ]^{2}\leq \lambda ^2x_{1}^{2}+\left ( 1- \lambda \right )^2y_{1}^{2}+2 \lambda\left ( 1- \lambda \right )\left ( x_{1}^{2}+y_{1}^{2} \right )$
$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq \lambda x_{1}^{2}+\left ( 1- \lambda \right )y_{1}^{2}$
$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq 8\lambda x_2+8\left ( 1- \lambda \right )y_2$
$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )y_1 \right ]^{2}\leq 8\left [\lambda x_2+\left ( 1- \lambda \right )y_2 \right ]$
$\Rightarrow \lambda x+\left ( 1- \lambda \right )y \in S$
步驟 3 - 證明集合 $S \in \mathbb{R}^n$ 是凸集當且僅當對於每個整數 k,S 的任意 k 個點的任意凸組合都在 S 中。
解答
設 S 為凸集。然後,要證明;
$c_1x_1+c_2x_2+.....+c_kx_k \in S, \displaystyle\sum\limits_{1}^k c_i=1,c_i\geq 0, \forall i \in 1,2,....,k$
用數學歸納法證明
對於 $k=1,x_1 \in S, c_1=1 \Rightarrow c_1x_1 \in S$
對於 $k=2,x_1,x_2 \in S, c_1+c_2=1$ 並且由於 S 是凸集
$\Rightarrow c_1x_1+c_2x_2 \in S.$
假設 S 的 m 個點的凸組合在 S 中,即
$c_1x_1+c_2x_2+...+c_mx_m \in S,\displaystyle\sum\limits_{1}^m c_i=1 ,c_i \geq 0, \forall i \in 1,2,...,m$
現在,設 $x_1,x_2....,x_m,x_{m+1} \in S$
設 $x=\mu_1x_1+\mu_2x_2+...+\mu_mx_m+\mu_{m+1}x_{m+1}$
設 $x=\left ( \mu_1+\mu_2+...+\mu_m \right )\frac{\mu_1x_1+\mu_2x_2+\mu_mx_m}{\mu_1+\mu_2+.........+\mu_m}+\mu_{m+1}x_{m+1}$
設 $y=\frac{\mu_1x_1+\mu_2x_2+...+\mu_mx_m}{\mu_1+\mu_2+.........+\mu_m}$
$\Rightarrow x=\left ( \mu_1+\mu_2+...+\mu_m \right )y+\mu_{m+1}x_{m+1}$
現在 $y \in S$,因為係數之和為 1。
$\Rightarrow x \in S$,因為 S 是凸集且 $y,x_{m+1} \in S$
因此,用數學歸納法證明。
凸最佳化 - 仿射集
如果對於任意兩點,經過這兩點的直線都位於集合 A 中,則稱集合 A 為仿射集。
注意 -
$S$ 是仿射集當且僅當它包含其所有點的仿射組合。
空集和單點集都是仿射集和凸集。
例如,線性方程的解集是仿射集。
證明
設 S 為線性方程的解集。
根據定義,$S=\left \{ x \in \mathbb{R}^n:Ax=b \right \}$
設 $x_1,x_2 \in S\Rightarrow Ax_1=b$ 且 $Ax_2=b$
要證明 : $A\left [ \theta x_1+\left ( 1-\theta \right )x_2 \right ]=b, \forall \theta \in\left ( 0,1 \right )$
$A\left [ \theta x_1+\left ( 1-\theta \right )x_2 \right ]=\theta Ax_1+\left ( 1-\theta \right )Ax_2=\theta b+\left ( 1-\theta \right )b=b$
因此 S 是仿射集。
定理
如果 C 是仿射集且 $x_0 \in C$,則集合 $V= C-x_0=\left \{ x-x_0:x \in C \right \}$ 是 C 的子空間。
證明
設 $x_1,x_2 \in V$
要證明:$\alpha x_1+\beta x_2 \in V$,對於某些 $\alpha,\beta$
現在,$x_1+x_0 \in C$ 且 $x_2+x_0 \in C$,根據 V 的定義
現在,$\alpha x_1+\beta x_2+x_0=\alpha \left ( x_1+x_0 \right )+\beta \left ( x_2+x_0 \right )+\left ( 1-\alpha -\beta \right )x_0$
但是 $\alpha \left ( x_1+x_0 \right )+\beta \left ( x_2+x_0 \right )+\left ( 1-\alpha -\beta \right )x_0 \in C$,因為 C 是仿射集。
因此,$\alpha x_1+\beta x_2 \in V$
因此得證。
凸最佳化 - 包
S 中一組點的凸包是包含 S 中所有點(在其內部或邊界上)的最小凸區域的邊界。
或
設 $S\subseteq \mathbb{R}^n$,S 的凸包,記為 $Co\left ( S \right )$,是 S 的所有凸組合的集合,即 $x \in Co\left ( S \right )$ 當且僅當 $x \in \displaystyle\sum\limits_{i=1}^n \lambda_ix_i$,其中 $\displaystyle\sum\limits_{1}^n \lambda_i=1$ 且 $\lambda_i \geq 0 \forall x_i \in S$
備註 - S 中一組點的凸包在平面上定義了一個凸多邊形,S 中位於多邊形邊界上的點定義了多邊形的頂點。
定理 $Co\left ( S \right )= \left \{ x:x=\displaystyle\sum\limits_{i=1}^n \lambda_ix_i,x_i \in S, \displaystyle\sum\limits_{i=1}^n \lambda_i=1,\lambda_i \geq 0 \right \}$ 證明凸包是凸集。
證明
設 $x_1,x_2 \in Co\left ( S \right )$,則 $x_1=\displaystyle\sum\limits_{i=1}^n \lambda_ix_i$ 且 $x_2=\displaystyle\sum\limits_{i=1}^n \lambda_\gamma x_i$,其中 $\displaystyle\sum\limits_{i=1}^n \lambda_i=1, \lambda_i\geq 0$ 且 $\displaystyle\sum\limits_{i=1}^n \gamma_i=1,\gamma_i\geq0$
對於 $\theta \in \left ( 0,1 \right ),\theta x_1+\left ( 1-\theta \right )x_2=\theta \displaystyle\sum\limits_{i=1}^n \lambda_ix_i+\left ( 1-\theta \right )\displaystyle\sum\limits_{i=1}^n \gamma_ix_i$
$\theta x_1+\left ( 1-\theta \right )x_2=\displaystyle\sum\limits_{i=1}^n \lambda_i \theta x_i+\displaystyle\sum\limits_{i=1}^n \gamma_i\left ( 1-\theta \right )x_i$
$\theta x_1+\left ( 1-\theta \right )x_2=\displaystyle\sum\limits_{i=1}^n\left [ \lambda_i\theta +\gamma_i\left ( 1-\theta \right ) \right ]x_i$
考慮係數,
$\displaystyle\sum\limits_{i=1}^n\left [ \lambda_i\theta +\gamma_i\left ( 1-\theta \right ) \right ]=\theta \displaystyle\sum\limits_{i=1}^n \lambda_i+\left ( 1-\theta \right )\displaystyle\sum\limits_{i=1}^n\gamma_i=\theta +\left ( 1-\theta \right )=1$
因此,$\theta x_1+\left ( 1-\theta \right )x_2 \in Co\left ( S \right )$
因此,凸包是凸集。
Caratheodory定理
設 S 為 $\mathbb{R}^n$ 中的任意集合。如果 $x \in Co\left ( S \right )$,則 $x \in Co\left ( x_1,x_2,....,x_n,x_{n+1} \right )$.
證明
由於 $x \in Co\left ( S\right )$,則 x 可以表示為 S 中有限多個點的凸組合,即
$x=\displaystyle\sum\limits_{j=1}^k \lambda_jx_j,\displaystyle\sum\limits_{j=1}^k \lambda_j=1, \lambda_j \geq 0$ 且 $x_j \in S, \forall j \in \left ( 1,k \right )$
如果 $k \leq n+1$,則顯然結果成立。
如果 $k \geq n+1$,則 $\left ( x_2-x_1 \right )\left ( x_3-x_1 \right ),....., \left ( x_k-x_1 \right )$ 線性相關。
$\Rightarrow \exists \mu _j \in \mathbb{R}, 2\leq j\leq k$(不全為零)使得 $\displaystyle\sum\limits_{j=2}^k \mu _j\left ( x_j-x_1 \right )=0$
定義 $\mu_1=-\displaystyle\sum\limits_{j=2}^k \mu _j$,則 $\displaystyle\sum\limits_{j=1}^k \mu_j x_j=0, \displaystyle\sum\limits_{j=1}^k \mu_j=0$
其中不全 $\mu_j$ 等於零。由於 $\displaystyle\sum\limits_{j=1}^k \mu_j=0$,因此至少有一個 $\mu_j > 0,1 \leq j \leq k$
然後,$x=\displaystyle\sum\limits_{1}^k \lambda_j x_j+0$
$x=\displaystyle\sum\limits_{1}^k \lambda_j x_j- \alpha \displaystyle\sum\limits_{1}^k \mu_j x_j$
$x=\displaystyle\sum\limits_{1}^k\left ( \lambda_j- \alpha\mu_j \right )x_j $
選擇 $\alpha$ 使得 $\alpha=min\left \{ \frac{\lambda_j}{\mu_j}, \mu_j\geq 0 \right \}=\frac{\lambda_j}{\mu _j},$ 對於某個 $i=1,2,...,k$
如果 $\mu_j\leq 0, \lambda_j-\alpha \mu_j\geq 0$
如果 $\mu_j> 0, then \:\frac{\lambda _j}{\mu_j}\geq \frac{\lambda_i}{\mu _i}=\alpha \Rightarrow \lambda_j-\alpha \mu_j\geq 0, j=1,2,...k$
特別是,$\lambda_i-\alpha \mu_i=0$,根據 $\alpha$ 的定義
$x=\displaystyle\sum\limits_{j=1}^k \left ( \lambda_j- \alpha\mu_j\right )x_j$,其中
$\lambda_j- \alpha\mu_j\geq0$ 且 $\displaystyle\sum\limits_{j=1}^k\left ( \lambda_j- \alpha\mu_j\right )=1$ 且 $\lambda_i- \alpha\mu_i=0$
因此,x 可以表示為最多 (k-1) 個點的凸組合。
這個化簡過程可以重複進行,直到 x 被表示為 (n+1) 個元素的凸組合。
凸最佳化 - 魏爾斯特拉斯定理
設 S 為 $\mathbb{R}^n$ 中一個非空、閉合且有界的集合(也稱為緊集),並設 $f:S\rightarrow \mathbb{R} $ 為 S 上的一個連續函式,則問題 min $\left \{ f\left ( x \right ):x \in S \right \}$ 取得其最小值。
證明
由於 S 非空且有界,因此存在下界。
$\alpha =Inf\left \{ f\left ( x \right ):x \in S \right \}$
現在設 $S_j=\left \{ x \in S:\alpha \leq f\left ( x \right ) \leq \alpha +\delta ^j\right \} \forall j=1,2,...$ 且 $\delta \in \left ( 0,1 \right )$
根據下確界的定義,對於每個 j,$S_j$ 都是非空的。
選擇一些 $x_j \in S_j$ 以獲得一個序列 $\left \{ x_j \right \}$,其中 j=1,2,...。
由於 S 有界,因此該序列也有界,並且存在一個收斂子序列 $\left \{ y_j \right \}$,它收斂於 $\hat{x}$。因此,$\hat{x}$ 是一個極限點,而 S 是閉合的,所以 $\hat{x} \in S$。由於 f 是連續的,所以 $f\left ( y_i \right )\rightarrow f\left ( \hat{x} \right )$。
由於 $\alpha \leq f\left ( y_i \right )\leq \alpha+\delta^k$,$\alpha=\displaystyle\lim_{k\rightarrow \infty}f\left ( y_i \right )=f\left ( \hat{x} \right )$
因此,$\hat{x}$ 是最小化解。
備註
魏爾斯特拉斯定理成立有兩個重要的必要條件。如下所示 -
**步驟 1** - 集合 S 應為有界集合。
考慮函式 f\left ( x \right )=x。
它是一個無界集合,並且在它定義域的任何點都沒有最小值。
因此,為了獲得最小值,S 應是有界的。
**步驟 2** - 集合 S 應為閉合的。
考慮函式 $f\left ( x \right )=\frac{1}{x}$,其定義域為 \left ( 0,1 \right )。
此函式在給定定義域中不是閉合的,並且它的最小值也不存在。
因此,為了獲得最小值,S 應為閉合的。
凸最佳化 - 最近點定理
設 S 為 $\mathbb{R}^n$ 中一個非空閉凸集,並設 $y\notin S$,則存在一個點 $\bar{x}\in S$,其到 y 的距離最小,即 $\left \| y-\bar{x} \right \| \leq \left \| y-x \right \| \forall x \in S.$
此外,$\bar{x}$ 是一個最小化點當且僅當 $\left ( y-\hat{x} \right )^{T}\left ( x-\hat{x} \right )\leq 0$ 或 $\left ( y-\hat{x}, x-\hat{x} \right )\leq 0$
證明
最近點的存在性
由於 $S\ne \phi$,存在一個點 $\hat{x}\in S$,使得 S 到 y 的最小距離小於或等於 $\left \| y-\hat{x} \right \|。
定義 $\hat{S}=S \cap \left \{ x:\left \| y-x \right \|\leq \left \| y-\hat{x} \right \| \right \}$
由於 $ \hat{S}$ 是閉合且有界的,並且由於範數是一個連續函式,因此根據魏爾斯特拉斯定理,存在一個最小點 $\hat{x} \in S$,使得 $\left \| y-\hat{x} \right \|=Inf\left \{ \left \| y-x \right \|,x \in S \right \}$
唯一性
假設 $\bar{x} \in S$,使得 $\left \| y-\hat{x} \right \|=\left \| y-\hat{x} \right \|= \alpha$
由於 S 是凸的,所以 $\frac{\hat{x}+\bar{x}}{2} \in S$
但是,$\left \| y-\frac{\hat{x}-\bar{x}}{2} \right \|\leq \frac{1}{2}\left \| y-\hat{x} \right \|+\frac{1}{2}\left \| y-\bar{x} \right \|=\alpha$
它不能是嚴格的不等式,因為 $\hat{x}$ 最接近 y。
因此,$\left \| y-\hat{x} \right \|=\mu \left \| y-\hat{x} \right \|,對於某些 $\mu$
現在 $\left \| \mu \right \|=1.$ 如果 $\mu=-1$,則 $\left ( y-\hat{x} \right )=-\left ( y-\hat{x} \right )\Rightarrow y=\frac{\hat{x}+\bar{x}}{2} \in S$
但是 $y \in S$。因此矛盾。因此 $\mu=1 \Rightarrow \hat{x}=\bar{x}$
因此,最小化點是唯一的。
對於證明的第二部分,假設 $\left ( y-\hat{x} \right )^{\tau }\left ( x-\bar{x} \right )\leq 0$ 對於所有 $x\in S$
現在,
$\left \| y-x \right \|^{2}=\left \| y-\hat{x}+ \hat{x}-x\right \|^{2}=\left \| y-\hat{x} \right \|^{2}+\left \|\hat{x}-x \right \|^{2}+2\left (\hat{x}-x \right )^{\tau }\left ( y-\hat{x} \right )$
$\Rightarrow \left \| y-x \right \|^{2}\geq \left \| y-\hat{x} \right \|^{2}$ 因為 $\left \| \hat{x}-x \right \|^{2}\geq 0$ 且 $\left ( \hat{x}- x\right )^{T}\left ( y-\hat{x} \right )\geq 0$
因此,$\hat{x}$ 是最小化點。
反之,假設 $\hat{x}$ 是最小化點。
$\Rightarrow \left \| y-x \right \|^{2}\geq \left \| y-\hat{x} \right \|^2 \forall x \in S$
由於 S 是凸集。
$\Rightarrow \lambda x+\left ( 1-\lambda \right )\hat{x}=\hat{x}+\lambda\left ( x-\hat{x} \right ) \in S$ 對於 $x \in S$ 且 $\lambda \in \left ( 0,1 \right )$
現在,$\left \| y-\hat{x}-\lambda\left ( x-\hat{x} \right ) \right \|^{2}\geq \left \| y-\hat{x} \right \|^2$
並且
$\left \| y-\hat{x}-\lambda\left ( x-\hat{x} \right ) \right \|^{2}=\left \| y-\hat{x} \right \|^{2}+\lambda^2\left \| x-\hat{x} \right \|^{2}-2\lambda\left ( y-\hat{x} \right )^{T}\left ( x-\hat{x} \right )$
$\Rightarrow \left \| y-\hat{x} \right \|^{2}+\lambda^{2}\left \| x-\hat{x} \right \|-2 \lambda\left ( y-\hat{x} \right )^{T}\left ( x-\hat{x} \right )\geq \left \| y-\hat{x} \right \|^{2}$
$\Rightarrow 2 \lambda\left ( y-\hat{x} \right )^{T}\left ( x-\hat{x} \right )\leq \lambda^2\left \| x-\hat{x} \right \|^2$
$\Rightarrow \left ( y-\hat{x} \right )^{T}\left ( x-\hat{x} \right )\leq 0$
因此得證。
基本分離定理
設 S 為 $\mathbb{R}^n$ 中一個非空閉凸集,且 $y \notin S$。則存在一個非零向量 p 和標量 $\beta$,使得 $p^T y>\beta$ 且 $p^T x < \beta$ 對於每個 $x \in S$
證明
由於 S 是非空閉凸集,且 $y \notin S$,因此根據最近點定理,存在一個唯一的最小化點 $\hat{x} \in S$,使得
$\left ( x-\hat{x} \right )^T\left ( y-\hat{x} \right )\leq 0 \forall x \in S$
設 $p=\left ( y-\hat{x} \right )\neq 0$ 且 $\beta=\hat{x}^T\left ( y-\hat{x} \right )=p^T\hat{x}$。
則 $\left ( x-\hat{x} \right )^T\left ( y-\hat{x} \right )\leq 0$
$\Rightarrow \left ( y-\hat{x} \right )^T\left ( x-\hat{x} \right )\leq 0$
$\Rightarrow \left ( y-\hat{x} \right )^Tx\leq \left ( y-\hat{x} \right )^T \hat{x}=\hat{x}^T\left ( y-\hat{x} \right )$ 即,$p^Tx \leq \beta$
此外,$p^Ty-\beta=\left ( y-\hat{x} \right )^Ty-\hat{x}^T \left ( y-\hat{x} \right )$
$=\left ( y-\hat{x} \right )^T \left ( y-x \right )=\left \| y-\hat{x} \right \|^{2}>0$
$\Rightarrow p^Ty> \beta$
此定理導致分離超平面。基於上述定理的超平面可以定義如下 -
設 $S_1$ 和 $S_2$ 為 $\mathbb{R}$ 的非空子集,且 $H=\left \{ X:A^TX=b \right \}$ 為一個超平面。
如果 $A^TX \leq b \forall X \in S_1$ 且 $A_TX \geq b \forall X \in S_2$,則稱超平面 H 分離 $S_1$ 和 $S_2$。
如果 $A^TX < b \forall X \in S_1$ 且 $A_TX > b \forall X \in S_2$,則稱超平面 H 嚴格分離 $S_1$ 和 $S_2$。
如果 $A^TX \leq b \forall X \in S_1$ 且 $A_TX \geq b+ \varepsilon \forall X \in S_2$,其中 $\varepsilon$ 為一個正標量,則稱超平面 H 強分離 $S_1$ 和 $S_2$。
凸最佳化 - 錐
如果 $x \in C\Rightarrow \lambda x \in C \forall \lambda \geq 0$,則稱 $\mathbb{R}^n$ 中一個非空集合 C 為頂點為 0 的錐。
如果一個集合 C 既是凸的又是錐,則稱其為凸錐。
例如,$y=\left | x \right |$ 不是凸錐,因為它不是凸的。
但是,$y \geq \left | x \right |$ 是一個凸錐,因為它既是凸的又是錐。
**注意** - 當且僅當對於任何 $x,y \in C$,$x+y \in C$ 時,錐 C 為凸的。
證明
由於 C 是錐,對於 $x,y \in C \Rightarrow \lambda x \in C$ 且 $\mu y \in C \:\forall \:\lambda, \mu \geq 0$
如果 $\lambda x + \left ( 1-\lambda \right )y \in C \: \forall \:\lambda \in \left ( 0, 1 \right )$,則 C 是凸的。
由於 C 是錐,$\lambda x \in C$ 且 $\left ( 1-\lambda \right )y \in C \Leftrightarrow x,y \in C$
因此,如果 $x+y \in C$,則 C 是凸的。
一般來說,如果 $x_1,x_2 \in C$,則 $\lambda_1x_1+\lambda_2x_2 \in C, \forall \lambda_1,\lambda_2 \geq 0$
示例
$\mathbb{R}^n$ 中無限多個向量的錐組合是一個凸錐。
任何空集都是一個凸錐。
任何線性函式都是一個凸錐。
由於超平面是線性的,因此它也是一個凸錐。
閉半空間也是凸錐。
**注意** - 兩個凸錐的交集是一個凸錐,但它們的並集可能是也可能不是凸錐。
凸最佳化 - 極錐
設 S 為 $\mathbb{R}^n$ 中一個非空集合,則 S 的極錐,記為 $S^*$,由 $S^*=\left \{p \in \mathbb{R}^n, p^Tx \leq 0 \: \forall x \in S \right \}$ 給出。
備註
即使 S 不是凸的,極錐也總是凸的。
如果 S 是空集,則 $S^*=\mathbb{R}^n$。
極性可以看作是正交性的推廣。
設 $C\subseteq \mathbb{R}^n$,則 C 的正交空間,記為 $C^\perp =\left \{ y \in \mathbb{R}^n:\left \langle x,y \right \rangle=0 \forall x \in C \right \}$。
引理
設 $S,S_1$ 和 $S_2$ 為 $\mathbb{R}^n$ 中的非空集合,則以下陳述為真 -
$S^*$ 是一個閉合凸錐。
$S \subseteq S^{**}$,其中 $S^{**}$ 是 $S^*$ 的極錐。
$S_1 \subseteq S_2 \Rightarrow S_{2}^{*} \subseteq S_{1}^{*}$。
證明
**步驟 1** - $S^*=\left \{ p \in \mathbb{R}^n,p^Tx\leq 0 \: \forall \:x \in S \right \}$
設 $x_1,x_2 \in S^*\Rightarrow x_{1}^{T}x\leq 0 $ 且 $x_{2}^{T}x \leq 0,\forall x \in S$
對於 $\lambda \in \left ( 0, 1 \right ),\left [ \lambda x_1+\left ( 1-\lambda \right )x_2 \right ]^Tx=\left [ \left ( \lambda x_1 \right )^T+ \left \{\left ( 1-\lambda \right )x_{2} \right \}^{T}\right ]x, \forall x \in S$
$=\left [ \lambda x_{1}^{T} +\left ( 1-\lambda \right )x_{2}^{T}\right ]x=\lambda x_{1}^{T}x+\left ( 1-\lambda \right )x_{2}^{T}\leq 0$
因此 $\lambda x_1+\left ( 1-\lambda \right )x_{2} \in S^*$
因此 $S^*$ 是一個凸集。
對於 $\lambda \geq 0,p^{T}x \leq 0, \forall \:x \in S$
因此,$\lambda p^T x \leq 0,$
$\Rightarrow \left ( \lambda p \right )^T x \leq 0$
$\Rightarrow \lambda p \in S^*$
因此,$S^*$ 是一個錐。
為了證明 $S^*$ 是閉合的,即要證明如果 $p_n \rightarrow p$ 當 $n \rightarrow \infty$ 時,則 $p \in S^*$
$\forall x \in S, p_{n}^{T}x-p^T x=\left ( p_n-p \right )^T x$
當 $p_n \rightarrow p$ 當 $n \rightarrow \infty \Rightarrow \left ( p_n \rightarrow p \right )\rightarrow 0$
因此 $p_{n}^{T}x \rightarrow p^{T}x$。但是 $p_{n}^{T}x \leq 0, \: \forall x \in S$
因此,$p^Tx \leq 0, \forall x \in S$
$\Rightarrow p \in S^*$
因此,$S^*$ 是閉合的。
**步驟 2** - $S^{**}=\left \{ q \in \mathbb{R}^n:q^T p \leq 0, \forall p \in S^*\right \}$
設 $x \in S$,則 $ \forall p \in S^*, p^T x \leq 0 \Rightarrow x^Tp \leq 0 \Rightarrow x \in S^{**}$
因此,$S \subseteq S^{**}$
**步驟 3** - $S_2^*=\left \{ p \in \mathbb{R}^n:p^Tx\leq 0, \forall x \in S_2 \right \}$
由於 $S_1 \subseteq S_2 \Rightarrow \forall x \in S_2 \Rightarrow \forall x \in S_1$
因此,如果 $\hat{p} \in S_2^*, $則 $\hat{p}^Tx \leq 0,\forall x \in S_2$
$\Rightarrow \hat{p}^Tx\leq 0, \forall x \in S_1$
$\Rightarrow \hat{p}^T \in S_1^*$
$\Rightarrow S_2^* \subseteq S_1^*$
定理
設 C 為非空閉凸錐,則 $C=C^**$
證明
根據之前的引理,$C=C^{**}$。
要證明:$x \in C^{**} \subseteq C$
設 $x \in C^{**}$ 且 $x \notin C$
然後根據基本分離定理,存在一個非零向量 p 和一個標量 α,使得 $p^Ty \leq \alpha, \forall y \in C$
因此,$p^Tx > \alpha$
但由於 $\left ( y=0 \right ) \in C$ 且 $p^Ty\leq \alpha, \forall y \in C \Rightarrow \alpha\geq 0$ 且 $p^Tx>0$
如果 $p \notin C^*$,則存在某個 $\bar{y} \in C$ 使得 $p^T \bar{y}>0$,並且透過取足夠大的 λ 可以使 $p^T\left ( \lambda \bar{y} \right )$ 任意大。
這與 $p^Ty \leq \alpha, \forall y \in C$ 的事實相矛盾。
因此,$p \in C^*$
由於 $x \in C^*=\left \{ q:q^Tp\leq 0, \forall p \in C^* \right \}$
因此,$x^Tp \leq 0 \Rightarrow p^Tx \leq 0$
但 $p^Tx> \alpha$
這是矛盾的。
因此,$x \in C$
因此 $C=C^{**}$。
凸最佳化 - 錐組合
形式為 $\alpha_1x_1+\alpha_2x_2+....+\alpha_nx_n$ 的點,其中 $\alpha_1, \alpha_2,...,\alpha_n\geq 0$,稱為 $x_1, x_2,...,x_n$ 的錐組合。
如果 $x_i$ 在凸錐 C 中,則 $x_i$ 的每個錐組合也在 C 中。
如果一個集合 C 包含其所有元素的錐組合,則 C 是一個凸錐。
錐包
錐包定義為給定集合 S 的所有錐組合的集合,記為 coni(S)。
因此,$coni\left ( S \right )=\left \{ \displaystyle\sum\limits_{i=1}^k \lambda_ix_i:x_i \in S,\lambda_i\in \mathbb{R}, \lambda_i\geq 0,i=1,2,...\right \}$
- 錐包是凸集。
- 原點始終屬於錐包。
凸最佳化 - 多面體集
如果 $\mathbb{R}^n$ 中的一個集合是有限個閉半空間的交集,則稱該集合為多面體集,即
$S=\left \{ x \in \mathbb{R}^n:p_{i}^{T}x\leq \alpha_i, i=1,2,....,n \right \}$
例如,
$\left \{ x \in \mathbb{R}^n:AX=b \right \}$
$\left \{ x \in \mathbb{R}^n:AX\leq b \right \}$
$\left \{ x \in \mathbb{R}^n:AX\geq b \right \}$
多面體錐
如果 $\mathbb{R}^n$ 中的一個集合是有限個包含原點的半空間的交集,則稱該集合為多面體錐,即 $S=\left \{ x \in \mathbb{R}^n:p_{i}^{T}x\leq 0, i=1, 2,... \right \}$
多胞體
多胞體是有界的多面體集。
備註
- 多胞體是有限個點的凸包。
- 多面體錐是由有限個向量生成的。
- 多面體集是閉集。
- 多面體集是凸集。
凸集的極點
設 S 是 $\mathbb{R}^n$ 中的凸集。如果 $x \in S$ 且 $x= \lambda x_1+\left ( 1-\lambda \right )x_2$,其中 $x_1, x_2 \in S$ 且 $\lambda \in\left ( 0, 1 \right )$ 蘊含 $x=x_1=x_2$,則稱 $x$ 為 S 的極點。
示例
步驟 1 − $S=\left \{ \left ( x_1,x_2 \right ) \in \mathbb{R}^2:x_{1}^{2}+x_{2}^{2}\leq 1 \right \}$
極點,$E=\left \{ \left ( x_1, x_2 \right )\in \mathbb{R}^2:x_{1}^{2}+x_{2}^{2}= 1 \right \}$
步驟 2 − $S=\left \{ \left ( x_1,x_2 \right )\in \mathbb{R}^2:x_1+x_2< 2, -x_1+2x_2\leq 2, x_1,x_2\geq 0 \right \}$
極點,$E=\left \{ \left ( 0, 0 \right), \left ( 2, 0 \right), \left ( 0, 1 \right), \left ( \frac{2}{3}, \frac{4}{3} \right) \right \}$
步驟 3 − S 是由點 $\left \{ \left ( 0,0 \right ), \left ( 1,1 \right ), \left ( 1,3 \right ), \left ( -2,4 \right ),\left ( 0,2 \right ) \right \}$ 組成的多胞體。
極點,$E=\left \{ \left ( 0,0 \right ), \left ( 1,1 \right ),\left ( 1,3 \right ),\left ( -2,4 \right ) \right \}$
備註
凸集 S 的任何點都可以表示為其極點的凸組合。
這僅適用於 $\mathbb{R}^n$ 中的閉有界集。
對於無界集,這可能不成立。
k 個極點
凸集中的一個點稱為 k 個極點當且僅當它是 S 內 k 維凸集的內點,並且它不是 S 內 (k+1) 維凸集的內點。基本上,對於凸集 S,k 個極點構成 k 維開面。
凸最佳化 - 方向
設 S 是 $\mathbb{R}^n$ 中的閉凸集。如果對於每個 $x \in S$,$x+\lambda d \in S, \forall \lambda \geq 0$,則非零向量 $d \in \mathbb{R}^n$ 稱為 S 的方向。
如果對於 $ \alpha>0$,$d \neq \alpha d_2$,則 S 的兩個方向 $d_1$ 和 $d_2$ 稱為不同的方向。
如果方向 d 不能寫成兩個不同方向的正線性組合,即如果 $d=\lambda _1d_1+\lambda _2d_2$,其中 $\lambda _1, \lambda _2>0$,則 $d_1= \alpha d_2$,其中 α 為某個數,則稱 S 的方向 d 為極方向。
任何其他方向都可以表示為極方向的正組合。
對於凸集 $S$,如果對於某個 $x \in S$ 和所有 $\lambda \geq0$,$x+\lambda d \in S$,則方向 d 稱為 $S$ 的**隱退方向**。
設 E 是某個函式 $f:S \rightarrow$ 在 $\mathbb{R}^n$ 中的非空凸集 S 上取得最大值的點的集合,則 E 稱為 S 的暴露面。暴露面的方向稱為暴露方向。
方向為極方向的射線稱為極射線。
示例
考慮函式 $f\left ( x \right )=y=\left |x \right |$,其中 $x \in \mathbb{R}^n$。設 d 是 $\mathbb{R}^n$ 中的單位向量。
則 d 是函式 f 的方向,因為對於任何 $\lambda \geq 0$,$x+\lambda d \in f\left ( x \right )$。
凸函式和凹函式
設 $f:S \rightarrow \mathbb{R}$,其中 S 是 $\mathbb{R}^n$ 中的非空凸集,則如果 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right ), \forall \lambda \in \left ( 0,1 \right )$,則稱 $f\left ( x \right )$ 在 S 上是凸的。
另一方面,設 $f:S\rightarrow \mathbb{R}$,其中 S 是 $\mathbb{R}^n$ 中的非空凸集,則如果 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\geq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right ), \forall \lambda \in \left ( 0, 1 \right )$,則稱 $f\left ( x \right )$ 在 S 上是凹的。
設 $f:S \rightarrow \mathbb{R}$,其中 S 是 $\mathbb{R}^n$ 中的非空凸集,則如果 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )< \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right ), \forall \lambda \in \left ( 0, 1 \right )$,則稱 $f\left ( x\right )$ 在 S 上是嚴格凸的。
設 $f:S \rightarrow \mathbb{R}$,其中 S 是 $\mathbb{R}^n$ 中的非空凸集,則如果 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )> \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right ), \forall \lambda \in \left ( 0, 1 \right )$,則稱 $f\left ( x\right )$ 在 S 上是嚴格凹的。
示例
線性函式既是凸函式又是凹函式。
$f\left ( x \right )=\left | x \right |$ 是凸函式。
$f\left ( x \right )= \frac{1}{x}$ 是凸函式。
定理
設 $f_1,f_2,...,f_k:\mathbb{R}^n \rightarrow \mathbb{R}$ 是凸函式。考慮函式 $f\left ( x \right )=\displaystyle\sum\limits_{j=1}^k \alpha_jf_j\left ( x \right )$,其中 $\alpha_j>0,j=1, 2, ...k,$ 則 $f\left ( x \right )$ 是凸函式。
證明
由於 $f_1,f_2,...f_k$ 是凸函式
因此,$f_i\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f_i\left ( x_1 \right )+\left ( 1-\lambda \right )f_i\left ( x_2 \right ), \forall \lambda \in \left ( 0, 1 \right )$ 且 $i=1, 2,....,k$
考慮函式 $f\left ( x \right )$。
因此,
$ f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )$
$=\displaystyle\sum\limits_{j=1}^k \alpha_jf_j\left ( \lambda x_1 +1-\lambda \right )x_2\leq \displaystyle\sum\limits_{j=1}^k\alpha_j\lambda f_j\left ( x_1 \right )+\left ( 1-\lambda \right )f_j\left ( x_2 \right )$
$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda \left ( \displaystyle\sum\limits_{j=1}^k \alpha _jf_j\left ( x_1 \right ) \right )+\left ( \displaystyle\sum\limits_{j=1}^k \alpha _jf_j\left ( x_2 \right ) \right )$
$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_2 \right )\leq \left ( 1-\lambda \right )f\left ( x_2 \right )$
因此,$f\left ( x\right )$ 是凸函式。
定理
設 $f\left ( x\right )$ 是凸集 $S\subset \mathbb{R}^n$ 上的凸函式,則 $f\left ( x\right )$ 在 S 上的區域性最小值是全域性最小值。
證明
設 $\hat{x}$ 是 $f\left ( x \right )$ 的區域性最小值,且 $\hat{x}$ 不是全域性最小值。
因此,存在 $\hat{x} \in S$ 使得 $f\left ( \bar{x} \right )< f\left ( \hat{x} \right )$
由於 $\hat{x}$ 是區域性最小值,因此存在鄰域 $N_\varepsilon \left ( \hat{x} \right )$ 使得 $f\left ( \hat{x} \right )\leq f\left ( x \right ), \forall x \in N_\varepsilon \left ( \hat{x} \right )\cap S$
但 $f\left ( x \right )$ 是 S 上的凸函式,因此對於 $\lambda \in \left ( 0, 1 \right )$
我們有 $\lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}\leq \lambda f\left ( \hat{x} \right )+\left ( 1-\lambda \right )f\left ( \bar{x} \right )$
$\Rightarrow \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}< \lambda f\left ( \hat{x} \right )+\left ( 1-\lambda \right )f\left (\hat{x} \right )$
$\Rightarrow \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x}< f\left (\hat{x} \right ), \forall \lambda \in \left ( 0,1 \right )$
但對於某個 $\lambda<1$ 但接近 1 的值,我們有
$\lambda \hat{x}+\left ( 1-\lambda \right )\bar{x} \in N_\varepsilon \left ( \hat{x} \right )\cap S$ 且 $f\left ( \lambda \hat{x}+\left ( 1-\lambda \right )\bar{x} \right )< f\left ( \bar{x} \right )$
這是矛盾的。
因此,$\bar{x}$ 是全域性最小值。
上圖
設 S 是 $\mathbb{R}^n$ 中的非空子集,設 $f:S \rightarrow \mathbb{R}$,則 f 的上圖記為 epi(f) 或 $E_f$,它是 $\mathbb{R}^n+1$ 的一個子集,定義為 $E_f=\left \{ \left ( x,\alpha \right ):x \in \mathbb{R}^n, \alpha \in \mathbb{R}, f\left ( x \right )\leq \alpha \right \}$
下圖
設 S 是 $\mathbb{R}^n$ 中的非空子集,設 $f:S \rightarrow \mathbb{R}$,則 f 的下圖記為 hyp(f) 或 $H_f=\left \{ \left ( x, \alpha \right ):x \in \mathbb{R}^n, \alpha \in \mathbb{R}^n, \alpha \in \mathbb{R}, f\left ( x \right )\geq \alpha \right \}$
定理
設 S 是 $\mathbb{R}^n$ 中的非空凸集,設 $f:S \rightarrow \mathbb{R}^n$,則 f 是凸的當且僅當其上圖 $E_f$ 是凸集。
證明
設 f 是凸函式。
要證明 $E_f$ 是凸集。
設 $\left ( x_1, \alpha_1 \right ),\left ( x_2, \alpha_2 \right ) \in E_f,\lambda \in\left ( 0, 1 \right )$
要證明 $\lambda \left ( x_1,\alpha_1 \right )+\left ( 1-\lambda \right )\left ( x_2, \alpha_2 \right ) \in E_f$
$\Rightarrow \left [ \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda \alpha_1+\left ( 1-\lambda \right )\alpha_2 \right ]\in E_f$
$f\left ( x_1 \right )\leq \alpha _1, f\left ( x_2\right )\leq \alpha _2$
因此,$f\left (\lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f \left ( x_2 \right )$
$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda \alpha_1+\left ( 1-\lambda \right )\alpha_2$
逆命題
假設 $E_f$ 是一個凸集。
要證明 f 是凸函式。
即,要證明如果 $x_1, x_2 \in S,\lambda \left ( 0, 1\right )$
$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$
假設 $x_1,x_2 \in S, \lambda \in \left ( 0, 1 \right ),f\left ( x_1 \right ), f\left ( x_2 \right ) \in \mathbb{R}$
由於 $E_f$ 是一個凸集,$\left ( \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )\right )f\left ( x_2 \right )\in E_f$
因此,$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$
凸最佳化 - Jensen 不等式
假設 S 是 $\mathbb{R}^n$ 中的一個非空凸集,且 $f:S \rightarrow \mathbb{R}^n$。則 f 是凸函式當且僅當對於每個整數 $k>0$
$x_1,x_2,...x_k \in S, \displaystyle\sum\limits_{i=1}^k \lambda_i=1, \lambda_i\geq 0, \forall i=1,2,s,k$,有 $f\left ( \displaystyle\sum\limits_{i=1}^k \lambda_ix_i \right )\leq \displaystyle\sum\limits_{i=1}^k \lambda _if\left ( x \right )$
證明
透過數學歸納法證明。
$k=1:x_1 \in S$ 因此 $f\left ( \lambda_1 x_1\right ) \leq \lambda_i f\left (x_1\right )$,因為 $\lambda_i=1$。
$k=2:\lambda_1+\lambda_2=1$ 且 $x_1, x_2 \in S$
因此,$\lambda_1x_1+\lambda_2x_2 \in S$
因此根據定義,$f\left ( \lambda_1 x_1 +\lambda_2 x_2 \right )\leq \lambda _1f\left ( x_1 \right )+\lambda _2f\left ( x_2 \right )$
假設該命題對於 $n < k$ 成立
因此,
$f\left ( \lambda_1 x_1+ \lambda_2 x_2+....+\lambda_k x_k\right )\leq \lambda_1 f\left (x_1 \right )+\lambda_2 f\left (x_2 \right )+...+\lambda_k f\left (x_k \right )$
$k=n+1:$ 假設 $x_1, x_2,....x_n,x_{n+1} \in S$ 且 $\displaystyle\sum\limits_{i=1}^{n+1}=1$
因此 $\mu_1x_1+\mu_2x_2+.......+\mu_nx_n+\mu_{n+1} x_{n+1} \in S$
因此,$f\left (\mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1} x_{n+1} \right )$
$=f\left ( \left ( \mu_1+\mu_2+...+\mu_n \right)\frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+\mu_3}+\mu_{n+1}x_{n+1} \right)$
$=f\left ( \mu_y+\mu_{n+1}x_{n+1} \right )$ 其中 $\mu=\mu_1+\mu_2+...+\mu_n$ 且
$y=\frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+...+\mu_n}$ 並且 $\mu_1+\mu_{n+1}=1,y \in S$
$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right ) \leq \mu f\left ( y \right )+\mu_{n+1} f\left ( x_{n+1} \right )$
$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right ) \leq$
$\left ( \mu_1+\mu_2+...+\mu_n \right )f\left ( \frac{\mu_1x_1+\mu_2x_2+...+\mu_nx_n}{\mu_1+\mu_2+...+\mu_n} \right )+\mu_{n+1}f\left ( x_{n+1} \right )$
$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n +\mu_{n+1}x_{n+1}\right )\leq \left ( \mu_1+ \mu_2+ ...+\mu_n \right )$
$\left [ \frac{\mu_1}{\mu_1+ \mu_2+ ...+\mu_n}f\left ( x_1 \right )+...+\frac{\mu_n}{\mu_1+ \mu_2+ ...+\mu_n}f\left ( x_n \right ) \right ]+\mu_{n+1}f\left ( x_{n+1} \right )$
$\Rightarrow f\left ( \mu_1x_1+\mu_2x_2+...+\mu_nx_n+\mu_{n+1}x_{n+1}\right )\leq \mu_1f\left ( x_1 \right )+\mu_2f\left ( x_2 \right )+....$
因此得證。
凸最佳化 - 可微函式
假設 S 是 $\mathbb{R}^n$ 中的一個非空開集,則 $f:S\rightarrow \mathbb{R}$ 在 $\hat{x} \in S$ 處可微,如果存在一個向量 $\bigtriangledown f\left ( \hat{x} \right )$(稱為梯度向量)和一個函式 $\alpha :\mathbb{R}^n\rightarrow \mathbb{R}$,使得
$f\left ( x \right )=f\left ( \hat{x} \right )+\bigtriangledown f\left ( \hat{x} \right )^T\left ( x-\hat{x} \right )+\left \| x=\hat{x} \right \|\alpha \left ( \hat{x}, x-\hat{x} \right ), \forall x \in S$ 其中
$\alpha \left (\hat{x}, x-\hat{x} \right )\rightarrow 0 \bigtriangledown f\left ( \hat{x} \right )=\left [ \frac{\partial f}{\partial x_1}\frac{\partial f}{\partial x_2}...\frac{\partial f}{\partial x_n} \right ]_{x=\hat{x}}^{T}$
定理
假設 S 是 $\mathbb{R}^n$ 中的一個非空、開凸集,且 $f:S\rightarrow \mathbb{R}$ 在 S 上可微。則 f 是凸函式當且僅當對於 $x_1,x_2 \in S, \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right ) \leq f\left ( x_1 \right )-f\left ( x_2 \right )$
證明
假設 f 是一個凸函式。即,對於 $x_1,x_2 \in S, \lambda \in \left ( 0, 1 \right )$
$f\left [ \lambda x_1+\left ( 1-\lambda \right )x_2 \right ]\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$
$ \Rightarrow f\left [ \lambda x_1+\left ( 1-\lambda \right )x_2 \right ]\leq \lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )+f\left ( x_2 \right )$
$ \Rightarrow\lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )\geq f\left ( x_2+\lambda \left ( x_1-x_2 \right ) \right )-f\left ( x_2 \right )$
$\Rightarrow \lambda \left ( f\left ( x_1 \right )-f\left ( x_2 \right ) \right )\geq f\left ( x_2 \right )+\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )\lambda +$
$\left \| \lambda \left ( x_1-x_2 \right ) \right \|\alpha \left ( x_2,\lambda\left (x_1 - x_2 \right )-f\left ( x_2 \right ) \right )$
其中 $\alpha\left ( x_2, \lambda\left (x_1 - x_2 \right ) \right )\rightarrow 0$ 當 $\lambda \rightarrow 0$
兩邊除以 $\lambda$,得到:
$f\left ( x_1 \right )-f\left ( x_2 \right ) \geq \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right )$
逆命題
假設對於 $x_1,x_2 \in S, \bigtriangledown f\left ( x_2 \right )^T \left ( x_1-x_2 \right ) \leq f\left ( x_1 \right )-f \left ( x_2 \right )$
要證明 f 是凸函式。
由於 S 是凸集,$x_3=\lambda x_1+\left (1-\lambda \right )x_2 \in S, \lambda \in \left ( 0, 1 \right )$
由於 $x_1, x_3 \in S$,因此
$f\left ( x_1 \right )-f \left ( x_3 \right ) \geq \bigtriangledown f\left ( x_3 \right )^T \left ( x_1 -x_3\right )$
$ \Rightarrow f\left ( x_1 \right )-f \left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T \left ( x_1 - \lambda x_1-\left (1-\lambda \right )x_2\right )$
$ \Rightarrow f\left ( x_1 \right )-f \left ( x_3 \right )\geq \left ( 1- \lambda\right )\bigtriangledown f\left ( x_3 \right )^T \left ( x_1 - x_2\right )$
由於 $x_2, x_3 \in S$,因此
$f\left ( x_2 \right )-f\left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-x_3 \right )$
$\Rightarrow f\left ( x_2 \right )-f\left ( x_3 \right )\geq \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-\lambda x_1-\left ( 1-\lambda \right )x_2 \right )$
$\Rightarrow f\left ( x_2 \right )-f\left ( x_3 \right )\geq \left ( -\lambda \right )\bigtriangledown f\left ( x_3 \right )^T\left ( x_1-x_2 \right )$
因此,結合上述等式,得到:
$\lambda \left ( f\left ( x_1 \right )-f\left ( x_3 \right ) \right )+\left ( 1- \lambda \right )\left ( f\left ( x_2 \right )-f\left ( x_3 \right ) \right )\geq 0$
$\Rightarrow f\left ( x_3\right )\leq \lambda f\left ( x_1 \right )+\left ( 1-\lambda \right )f\left ( x_2 \right )$
定理
假設 S 是 $\mathbb{R}^n$ 中的一個非空開凸集,且 $f:S \rightarrow \mathbb{R}$ 在 S 上可微,則 f 在 S 上是凸函式當且僅當對於任意 $x_1,x_2 \in S,\left ( \bigtriangledown f \left ( x_2 \right )-\bigtriangledown f \left ( x_1 \right ) \right )^T \left ( x_2-x_1 \right ) \geq 0$
證明
假設 f 是一個凸函式,則利用之前的定理:
$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )\leq f\left ( x_1 \right )-f\left ( x_2 \right )$ 且
$\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq f\left ( x_2 \right )-f\left ( x_1 \right )$
將上述兩個等式相加,得到:
$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )+\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq 0$
$\Rightarrow \left ( \bigtriangledown f\left ( x_2 \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x_1-x_2 \right )\leq 0$
$\Rightarrow \left ( \bigtriangledown f\left ( x_2 \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x_2-x_1 \right )\geq 0$
逆命題
假設對於任意 $x_1,x_2 \in S,\left (\bigtriangledown f \left ( x_2\right )- \bigtriangledown f \left ( x_1\right )\right )^T \left ( x_2-x_1\right )\geq 0$
要證明 f 是凸函式。
假設 $x_1,x_2 \in S$,則根據中值定理,$\frac{f\left ( x_1\right )-f\left ( x_2\right )}{x_1-x_2}=\bigtriangledown f\left ( x\right ),x \in \left ( x_1-x_2\right ) \Rightarrow x= \lambda x_1+\left ( 1-\lambda\right )x_2$,因為 S 是一個凸集。
$\Rightarrow f\left ( x_1 \right )- f\left ( x_2 \right )=\left ( \bigtriangledown f\left ( x \right )^T \right )\left ( x_1-x_2 \right )$
對於 $x,x_1$,我們知道:
$\left ( \bigtriangledown f\left ( x \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( x-x_1 \right )\geq 0$
$\Rightarrow \left ( \bigtriangledown f\left ( x \right )-\bigtriangledown f\left ( x_1 \right ) \right )^T\left ( \lambda x_1+\left ( 1-\lambda \right )x_2-x_1 \right )\geq 0$
$\Rightarrow \left ( \bigtriangledown f\left ( x \right )- \bigtriangledown f\left ( x_1 \right )\right )^T\left ( 1- \lambda \right )\left ( x_2-x_1 \right )\geq 0$
$\Rightarrow \bigtriangledown f\left ( x \right )^T\left ( x_2-x_1 \right )\geq \bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )$
結合上述等式,得到:
$\Rightarrow \bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\leq f\left ( x_2 \right )-f\left ( x_1 \right )$
因此,利用最後一個定理,f 是一個凸函式。
二階可微函式
假設 S 是 $\mathbb{R}^n$ 的一個非空子集,且 $f:S\rightarrow \mathbb{R}$,則 f 在 $\bar{x} \in S$ 處二階可微,如果存在一個向量 $\bigtriangledown f\left (\bar{x}\right )$、一個 $n \times n$ 矩陣 $H\left (x\right )$(稱為Hessian矩陣) 和一個函式 $\alpha:\mathbb{R}^n \rightarrow \mathbb{R}$,使得 $f\left ( x \right )=f\left ( \bar{x}+x-\bar{x} \right )=f\left ( \bar{x} \right )+\bigtriangledown f\left ( \bar{x} \right )^T\left ( x-\bar{x} \right )+\frac{1}{2}\left ( x-\bar{x} \right )H\left ( \bar{x} \right )\left ( x-\bar{x} \right )$
其中 $ \alpha \left ( \bar{x}, x-\bar{x} \right )\rightarrow Oasx\rightarrow \bar{x}$
全域性最優的充分必要條件
定理
設 f 是一個二階可微函式。如果 $\bar{x}$ 是一個區域性最小值點,則 $\bigtriangledown f\left ( \bar{x} \right )=0$ 且 Hessian 矩陣 $H\left ( \bar{x} \right )$ 是半正定的。
證明
設 $d \in \mathbb{R}^n$。由於 f 在 $\bar{x}$ 處二階可微。
因此,
$f\left ( \bar{x} +\lambda d\right )=f\left ( \bar{x} \right )+\lambda \bigtriangledown f\left ( \bar{x} \right )^T d+\lambda^2d^TH\left ( \bar{x} \right )d+\lambda^2d^TH\left ( \bar{x} \right )d+$
$\lambda^2\left \| d \right \|^2\beta \left ( \bar{x}, \lambda d \right )$
但 $\bigtriangledown f\left ( \bar{x} \right )=0$ 且 $\beta\left ( \bar{x}, \lambda d \right )\rightarrow 0$ 當 $\lambda \rightarrow 0$
$\Rightarrow f\left ( \bar{x} +\lambda d \right )-f\left ( \bar{x} \right )=\lambda ^2d^TH\left ( \bar{x} \right )d$
由於 $\bar{x }$ 是一個區域性最小值點,存在一個 $\delta > 0$ 使得 $f\left ( x \right )\leq f\left ( \bar{x}+\lambda d \right ), \forall \lambda \in \left ( 0,\delta \right )$
定理
設 $f:S \rightarrow \mathbb{R}^n$,其中 $S \subset \mathbb{R}^n$ 在 S 上二階可微。如果 $\bigtriangledown f\left ( x\right )=0$ 且 $H\left ( \bar{x} \right )$ 對所有 $x \in S$ 都是半正定的,則 $\bar{x}$ 是一個全域性最優解。
證明
由於 $H\left ( \bar{x} \right )$ 是半正定的,f 是 S 上的凸函式。由於 f 在 $\bar{x}$ 處可微且凸
$\bigtriangledown f\left ( \bar{x} \right )^T \left ( x-\bar{x} \right ) \leq f\left (x\right )-f\left (\bar{x}\right ),\forall x \in S$
由於 $\bigtriangledown f\left ( \bar{x} \right )=0, f\left ( x \right )\geq f\left ( \bar{x} \right )$
因此,$\bar{x}$ 是一個全域性最優解。
定理
假設 $\bar{x} \in S$ 是問題 $f:S \rightarrow \mathbb{R}$ 的區域性最優解,其中 S 是 $\mathbb{R}^n$ 的非空子集,且 S 是凸的。$min \:f\left ( x \right )$,其中 $x \in S$。
則
$\bar{x}$ 是一個全域性最優解。
如果 $\bar{x}$ 是嚴格區域性最小值點或 f 是嚴格凸函式,則 $\bar{x}$ 是唯一的全域性最優解,也是嚴格區域性最小值點。
證明
設 $\bar{x}$ 是問題的另一個全域性最優解,使得 $x \neq \bar{x}$ 且 $f\left ( \bar{x} \right )=f\left ( \hat{x} \right )$
由於 $\hat{x},\bar{x} \in S$ 且 S 是凸的,則 $\frac{\hat{x}+\bar{x}}{2} \in S$ 且 f 是嚴格凸的。
$\Rightarrow f\left ( \frac{\hat{x}+\bar{x}}{2} \right )< \frac{1}{2} f\left (\bar{x}\right )+\frac{1}{2} f\left (\hat{x}\right )=f\left (\hat{x}\right )$
這是矛盾的。
因此,$\hat{x}$ 是唯一的全域性最優解。
推論
設 $f:S \subset \mathbb{R}^n \rightarrow \mathbb{R}$ 是一個可微凸函式,其中 $\phi \neq S\subset \mathbb{R}^n$ 是一個凸集。考慮問題 $min f\left (x\right ),x \in S$,則 $\bar{x}$ 是一個最優解,當且僅當 $\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right ) \geq 0,\forall x \in S.$
證明
設 $\bar{x}$ 是一個最優解,即 $f\left (\bar{x}\right )\leq f\left (x\right ),\forall x \in S$
$\Rightarrow f\left (x\right )=f\left (\bar{x}\right )\geq 0$
$f\left (x\right )=f\left (\bar{x}\right )+\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right )+\left \| x-\bar{x} \right \|\alpha \left ( \bar{x},x-\bar{x} \right )$
其中 $\alpha \left ( \bar{x},x-\bar{x} \right )\rightarrow 0$ 當 $x \rightarrow \bar{x}$
$\Rightarrow f\left (x\right )-f\left (\bar{x}\right )=\bigtriangledown f\left (\bar{x}\right )^T\left (x-\bar{x}\right )\geq 0$
推論
設 f 是一個在 $\bar{x}$ 處可微的凸函式,則 $\bar{x}$ 是全域性最小值點當且僅當 $\bigtriangledown f\left (\bar{x}\right )=0$
示例
$f\left (x\right )=\left (x^2-1\right )^{3}, x \in \mathbb{R}$。
$\bigtriangledown f\left (x\right )=0 \Rightarrow x= -1,0,1$。
$\bigtriangledown^2f\left (\pm 1 \right )=0, \bigtriangledown^2 f\left (0 \right )=6>0$。
$f\left (\pm 1 \right )=0,f\left (0 \right )=-1$
因此,$f\left (x \right ) \geq -1=f\left (0 \right )\Rightarrow f\left (0 \right ) \leq f \left (x \right)\forall x \in \mathbb{R}$
$f\left (x \right )=x\log x$ 定義在 $S=\left \{ x \in \mathbb{R}, x> 0 \right \}$ 上。
${f}'x=1+\log x$
${f}''x=\frac{1}{x}>0$
因此,此函式是嚴格凸的。
$f \left (x \right )=e^{x},x \in \mathbb{R}$ 是嚴格凸的。
擬凸函式和擬凹函式
設 $f:S \rightarrow \mathbb{R}$,其中 $S \subset \mathbb{R}^n$ 是一個非空凸集。如果對於每個 $x_1,x_2 \in S$,都有 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq max\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \},\lambda \in \left ( 0, 1 \right )$,則稱函式 f 為擬凸函式。
例如,$f\left ( x \right )=x^{3}$
設 $f:S\rightarrow R $,其中 $S\subset \mathbb{R}^n$ 是一個非空凸集。如果對於每個 $x_1, x_2 \in S$,都有 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\geq min\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}, \lambda \in \left ( 0, 1 \right )$,則稱函式 f 為擬凹函式。
備註
- 每個凸函式都是擬凸函式,但反之不成立。
- 既是擬凸函式又是擬凹函式的函式稱為擬單調函式。
定理
設 $f:S\rightarrow \mathbb{R}$ 且 S 是 $\mathbb{R}^n$ 中的非空凸集。函式 f 是擬凸函式當且僅當 $S_{\alpha} =\left ( x \in S:f\left ( x \right )\leq \alpha \right \}$ 對每個實數 \alpha 都是凸的。
證明
設 f 在 S 上是擬凸的。
設 $x_1,x_2 \in S_{\alpha}$,因此 $x_1,x_2 \in S$ 且 $max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\leq \alpha$
設 $\lambda \in \left (0, 1 \right )$ 且設 $x=\lambda x_1+\left ( 1-\lambda \right )x_2\leq max \left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}\Rightarrow x \in S$
因此,$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}\leq \alpha$
因此,$S_{\alpha}$ 是凸的。
逆命題
設 $S_{\alpha}$ 對每個 $\alpha$ 都是凸的
$x_1,x_2 \in S, \lambda \in \left ( 0,1\right )$
$x=\lambda x_1+\left ( 1-\lambda \right )x_2$
設 $x=\lambda x_1+\left ( 1-\lambda \right )x_2$
對於 $x_1, x_2 \in S_{\alpha}, \alpha= max \left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}$
$\Rightarrow \lambda x_1+\left (1-\lambda \right )x_2 \in S_{\alpha}$
$\Rightarrow f \left (\lambda x_1+\left (1-\lambda \right )x_2 \right )\leq \alpha$
因此得證。
定理
設 $f:S\rightarrow \mathbb{R}$ 且 S 是 $\mathbb{R}^n$ 中的非空凸集。函式 f 是擬凹函式當且僅當 $S_{\alpha} =\left \{ x \in S:f\left ( x \right )\geq \alpha \right \}$ 對每個實數 $\alpha$ 都是凸的。
定理
設 $f:S\rightarrow \mathbb{R}$ 且 S 是 $\mathbb{R}^n$ 中的非空凸集。函式 f 是擬單調函式當且僅當 $S_{\alpha} =\left \{ x \in S:f\left ( x \right )= \alpha \right \}$ 對每個實數 $\alpha$ 都是凸的。
可微擬凸函式
定理
設 S 是 $\mathbb{R}^n$ 中的非空凸集,且 $f:S \rightarrow \mathbb{R}$ 在 S 上可微,則 f 是擬凸函式當且僅當對於任意 $x_1,x_2 \in S$ 且 $f\left ( x_1 \right )\leq f\left ( x_2 \right )$,都有 $\bigtriangledown f\left ( x_2 \right )^T\left ( x_2-x_1 \right )\leq 0$
證明
設 f 是一個擬凸函式。
設 $x_1,x_2 \in S$ 使得 $f\left ( x_1 \right ) \leq f\left ( x_2 \right )$
根據 f 在 $x_2$ 處的可微性,$\lambda \in \left ( 0, 1 \right )$
$f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )=f\left ( x_2+\lambda \left (x_1-x_2 \right ) \right )=f\left ( x_2 \right )+\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$
$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1-x_2 \right ) \right )$
$\Rightarrow f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )-f\left ( x_2 \right )-f\left ( x_2 \right )=\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )$
$+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x2, \lambda\left ( x_1-x_2 \right )\right )$
但由於 f 是擬凸的,$f \left ( \lambda x_1+ \left ( 1- \lambda \right )x_2 \right )\leq f \left (x_2 \right )$
$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right )+\lambda \left \| x_1-x_2 \right \|\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right ) \right )\leq 0$
但 $\alpha \left ( x_2,\lambda \left ( x_1,x_2 \right )\right )\rightarrow 0$ 當 $\lambda \rightarrow 0$
因此,$\bigtriangledown f\left ( x_2 \right )^T\left ( x_1-x_2 \right ) \leq 0$
逆命題
設對於 $x_1,x_2 \in S$ 且 $f\left ( x_1 \right )\leq f\left ( x_2 \right )$,$\bigtriangledown f\left ( x_2 \right )^T \left ( x_1,x_2 \right ) \leq 0$
要證明 f 是擬凸的,即 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )\leq f\left ( x_2 \right )$
反證法
假設存在一個 $x_3= \lambda x_1+\left ( 1-\lambda \right )x_2$ 使得 $f\left ( x_2 \right )< f \left ( x_3 \right )$ 對於某些 $ \lambda \in \left ( 0, 1 \right )$
對於 $x_2$ 和 $x_3$,$\bigtriangledown f\left ( x_3 \right )^T \left ( x_2-x_3 \right ) \leq 0$
$\Rightarrow -\lambda \bigtriangledown f\left ( x_3 \right )^T\left ( x_2-x_3 \right )\leq 0$
$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\geq 0$
對於 $x_1$ 和 $x_3$,$\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_3 \right ) \leq 0$
$\Rightarrow \left ( 1- \lambda \right )\bigtriangledown f\left ( x_3 \right )^T\left ( x_1-x_2 \right )\leq 0$
$\Rightarrow \bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )\leq 0$
因此,根據上述等式,$\bigtriangledown f\left ( x_3 \right )^T \left ( x_1-x_2 \right )=0$
定義 $U=\left \{ x:f\left ( x \right )\leq f\left ( x_2 \right ),x=\mu x_2+\left ( 1-\mu \right )x_3, \mu \in \left ( 0,1 \right ) \right \}$
因此,我們可以找到 $x_0 \in U$ 使得 $x_0 = \mu_0 x_2= \mu x_2+\left ( 1- \mu \right )x_3$ 對於某些 $\mu _0 \in \left ( 0,1 \right )$,它最接近 $x_3$,並且 $\hat{x} \in \left ( x_0,x_1 \right )$ 使得根據中值定理,
$$\frac{f\left ( x_3\right )-f\left ( x_0\right )}{x_3-x_0}= \bigtriangledown f\left ( \hat{x}\right )$$
$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\bigtriangledown f\left ( \hat{x} \right )^T\left ( x_3-x_0 \right )$$
$$\Rightarrow f\left ( x_3 \right )=f\left ( x_0 \right )+\mu_0 \lambda f\left ( \hat{x}\right )^T \left ( x_1-x_2 \right )$$
由於 $x_0$ 是 $x_1$ 和 $x_2$ 的組合,並且 $f\left (x_2 \right )< f\left ( \hat{x}\right )$
透過重複起始過程,$\bigtriangledown f \left ( \hat{x}\right )^T \left ( x_1-x_2\right )=0$
因此,結合上述等式,我們得到
$$f\left ( x_3\right )=f\left ( x_0 \right ) \leq f\left ( x_2\right )$$
$$\Rightarrow f\left ( x_3\right )\leq f\left ( x_2\right )$$
因此,這是一個矛盾。
示例
步驟 1 − $f\left ( x\right )=X^3$
$設 f \left ( x_1\right )\leq f\left ( x_2\right )$
$\Rightarrow x_{1}^{3}\leq x_{2}^{3}\Rightarrow x_1\leq x_2$
$\bigtriangledown f\left ( x_2 \right )\left ( x_1-x_2 \right )=3x_{2}^{2}\left ( x_1-x_2 \right )\leq 0$
因此,$f\left ( x\right )$ 是擬凸的。
步驟 2 − $f\left ( x\right )=x_{1}^{3}+x_{2}^{3}$
設 $\hat{x_1}=\left ( 2, -2\right )$ 和 $\hat{x_2}=\left ( 1, 0\right )$
因此,$f\left ( \hat{x_1}\right )=0,f\left ( \hat{x_2}\right )=1 \Rightarrow f\left ( \hat{x_1}\right )\setminus < f \left ( \hat{x_2}\right )$
因此,$\bigtriangledown f \left ( \hat{x_2}\right )^T \left ( \hat{x_1}- \hat{x_2}\right )= \left ( 3, 0\right )^T \left ( 1, -2\right )=3 >0$
因此 $f\left ( x\right )$ 不是擬凸的。
嚴格擬凸函式
設 $f:S\rightarrow \mathbb{R}^n$,且 S 是 $\mathbb{R}^n$ 中的一個非空凸集,則如果對於每個 $x_1,x_2 \in S$ 且 $f\left ( x_1 \right ) \neq f\left ( x_2 \right )$,都有 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )< max \:\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \}$,則稱 f 為嚴格擬凸函式。
備註
- 每個嚴格擬凸函式都是嚴格凸函式。
- 嚴格擬凸函式不蘊含擬凸性。
- 嚴格擬凸函式可能不是強擬凸函式。
- 偽凸函式是嚴格擬凸函式。
定理
設 $f:S\rightarrow \mathbb{R}^n$ 是嚴格擬凸函式,且 S 是 $\mathbb{R}^n$ 中的一個非空凸集。考慮問題:$min \:f\left ( x \right ), x \in S$。如果 $\hat{x}$ 是區域性最優解,則 $\bar{x}$ 是全域性最優解。
證明
假設存在 $ \bar{x} \in S$ 使得 $f\left ( \bar{x}\right )\leq f \left ( \hat{x}\right )$。
由於 $\bar{x},\hat{x} \in S$ 且 S 是凸集,因此,
$$\lambda \bar{x}+\left ( 1-\lambda \right )\hat{x}\in S, \forall \lambda \in \left ( 0,1 \right )$$
由於 $\hat{x}$ 是區域性最小值,所以 $f\left ( \hat{x} \right ) \leq f\left ( \lambda \bar{x}+\left ( 1-\lambda \right )\hat{x} \right ), \forall \lambda \in \left ( 0,\delta \right )$。
由於 f 是嚴格擬凸函式。
$$f\left ( \lambda \bar{x}+\left ( 1-\lambda \right )\hat{x} \right )< max \left \{ f\left ( \hat{x} \right ),f\left ( \bar{x} \right ) \right \}=f\left ( \hat{x} \right )$$
因此,這是一個矛盾。
嚴格擬凹函式
設 $f:S\rightarrow \mathbb{R}^n$,且 S 是 $\mathbb{R}^n$ 中的一個非空凸集,則如果對於每個 $x_1,x_2 \in S$ 且 $f\left (x_1\right )\neq f\left (x_2\right )$,都有
$$f\left (\lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$$.
示例
$f\left (x\right )=x^2-2$
這是一個嚴格擬凸函式,因為如果我們在滿足定義中約束條件的域中取任意兩點 $x_1,x_2$,則有 $f\left (\lambda x_1+\left (1- \lambda\right )x_2\right )< max \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$。因為該函式在負 x 軸上遞減,在正 x 軸上遞增(因為它是拋物線)。
$f\left (x\right )=-x^2$
這不是一個嚴格擬凸函式,因為如果我們取 $x_1=1$ 和 $x_2=-1$ 以及 $\lambda=0.5$,則 $f\left (x_1\right )=-1=f\left (x_2\right )$,但 $f\left (\lambda x_1+\left (1- \lambda\right )x_2\right )=0$。因此它不滿足定義中陳述的條件。但它是一個擬凹函式,因為如果我們在滿足定義中約束條件的域中取任意兩點,則有 $f\left ( \lambda x_1+\left (1-\lambda\right )x_2\right )> min \left \{ f \left (x_1\right ),f\left (x_2\right )\right \}$。因為該函式在負 x 軸上遞增,在正 x 軸上遞減。
強擬凸函式
設 $f:S\rightarrow \mathbb{R}^n$,且 S 是 $\mathbb{R}^n$ 中的一個非空凸集,則如果對於任何 $x_1,x_2 \in S$ 且 $\left ( x_1 \right ) \neq \left ( x_2 \right )$,都有 $f\left ( \lambda x_1+\left ( 1-\lambda \right )x_2 \right )< max \:\left \{ f\left ( x_1 \right ),f\left ( x_2 \right ) \right \},\forall \lambda \in \left ( 0,1\right )$,則稱 f 為強擬凸函式。
定理
如果 $\mathbb{R}^n$ 中非空凸集 S 上的擬凸函式 $f:S\rightarrow \mathbb{R}^n$ 在連線 S 的任意兩點的線段上不恆定,則該函式是強擬凸函式。
證明
設 f 是擬凸函式,且它在連線 S 的任意兩點的線段上不恆定。
假設 f 不是強擬凸函式。
存在 $x_1,x_2 \in S$ 且 $x_1 \neq x_2$,使得
$$f\left ( z \right )\geq max\left \{ f\left ( x_1 \right ), f\left ( x_2 \right ) \right \}, \forall z= \lambda x_1+\left ( 1-\lambda \right )x_2, \lambda \in \left ( 0,1 \right )$$
$\Rightarrow f\left ( x_1 \right )\leq f\left ( z \right )$ 且 $f\left ( x_2 \right )\leq f\left ( z \right )$
由於 f 在 $\left [ x_1,z \right ]$ 和 $\left [z,x_2 \right ] $ 上不恆定
所以存在 $u \in \left [ x_1,z \right ]$ 和 $v=\left [ z,x_2 \right ]$
$$\Rightarrow u= \mu_1x_1+\left ( 1-\mu_1\right )z,v=\mu_2z+\left ( 1- \mu_2\right )x_2$$
由於 f 是擬凸函式,
$$\Rightarrow f\left ( u \right )\leq max\left \{ f\left ( x_1 \right ),f \left ( z \right ) \right \}=f\left ( z \right )\:\: and \:\:f \left ( v \right ) \leq max \left \{ f\left ( z \right ),f\left ( x_2 \right ) \right \}$$
$$\Rightarrow f\left ( u \right )\leq f\left ( z \right ) \:\: and \:\: f\left ( v \right )\leq f\left ( z \right )$$
$$\Rightarrow max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$$
但 z 是 u 和 v 之間的任意一點,如果其中任何一個相等,則 f 為常數。
因此,$max \left \{ f\left ( u \right ),f\left ( v \right ) \right \} \leq f\left ( z \right )$
這與 f 的擬凸性相矛盾,因為 $z \in \left [ u,v \right ]$。
因此,f 是強擬凸函式。
定理
設 $f:S\rightarrow \mathbb{R}^n$,且 S 是 $\mathbb{R}^n$ 中的一個非空凸集。如果 $\hat{x}$ 是區域性最優解,則 $\hat{x}$ 是唯一的全域性最優解。
證明
由於強擬凸函式也是嚴格擬凸函式,因此區域性最優解是全域性最優解。
唯一性 − 設 f 在兩點 $u,v \in S$ 處取得全域性最優解
$$\Rightarrow f\left ( u \right ) \leq f\left ( x \right ).\forall x \in S\:\: and \:\:f\left ( v \right ) \leq f\left ( x \right ).\forall x \in S$$
如果 u 是全域性最優解,則 $f\left ( u \right )\leq f\left ( v \right )$ 且 $f\left ( v \right )\leq f\left ( u\right )\Rightarrow f\left ( u \right )=f\left ( v\right )$
$$f\left ( \lambda u+\left ( 1-\lambda\right )v\right )< max \left \{f\left ( u \right ),f\left ( v \right ) \right \}=f\left ( u \right )$$
這是矛盾的。
因此,只有一個全域性最優解。
備註
- 強擬凸函式也是嚴格擬凸函式。
- 嚴格凸函式可能是也可能不是強擬凸函式。
- 可微的嚴格凸函式是強擬凸函式。
偽凸函式
設 $f:S\rightarrow \mathbb{R}$ 是一個可微函式,且 S 是 $\mathbb{R}^n$ 中的一個非空凸集,則如果對於每個 $x_1,x_2 \in S$ 且 $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$,都有 $f\left ( x_2 \right )\geq f\left ( x_1 \right )$,或者等價地,如果 $f\left ( x_1 \right )>f\left ( x_2 \right )$,則 $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )<0$,則稱 f 為偽凸函式。
偽凹函式
設 $f:S\rightarrow \mathbb{R}$ 是一個可微函式,且 S 是 $\mathbb{R}^n$ 中的一個非空凸集,則如果對於每個 $x_1, x_2 \in S$ 且 $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$,都有 $f\left ( x_2 \right )\leq f\left ( x_1 \right )$,或者等價地,如果 $f\left ( x_1 \right )>f\left ( x_2 \right )$,則 $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )>0$,則稱 f 為偽凹函式。
備註
如果一個函式既是偽凸函式又是偽凹函式,則稱其為偽線性函式。
可微凸函式也是偽凸函式。
偽凸函式可能不是凸函式。例如,
$f\left ( x \right )=x+x^3$ 不是凸函式。如果 $x_1 \leq x_2,x_{1}^{3} \leq x_{2}^{3}$
因此,$\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )=\left ( 1+3x_{1}^{2} \right )\left ( x_2-x_1 \right ) \geq 0$
並且,$f\left ( x_2 \right )-f\left ( x_1 \right )=\left ( x_2-x_1 \right )+\left ( x_{2}^{3} -x_{1}^{3}\right )\geq 0$
$\Rightarrow f\left ( x_2 \right )\geq f\left ( x_1 \right )$
因此,它是偽凸函式。
偽凸函式是嚴格擬凸函式。因此,偽凸函式的每個區域性最小值也是全域性最小值。
嚴格偽凸函式
設 $f:S\rightarrow \mathbb{R}$ 是一個可微函式,且 S 是 $\mathbb{R}^n$ 中的一個非空凸集,則如果對於每個 $x_1,x_2 \in S$ 且 $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )\geq 0$,都有 $f\left ( x_2 \right )> f\left ( x_1 \right )$,或者等價地,如果 $f\left ( x_1 \right )\geq f\left ( x_2 \right )$,則 $\bigtriangledown f\left ( x_1 \right )^T\left ( x_2-x_1 \right )<0$,則稱 f 為嚴格偽凸函式。
定理
設 f 是偽凸函式,並假設對於某個 $\hat{x} \in S$,$\bigtriangledown f\left ( \hat{x}\right )=0$,則 $\hat{x}$ 是 f 在 S 上的全域性最優解。
證明
設 $\hat{x}$ 是 f 的臨界點,即 $\bigtriangledown f\left ( \hat{x}\right )=0$
由於 f 是偽凸函式,對於 $x \in S,$ 我們有
$$\bigtriangledown f\left ( \hat{x}\right )\left ( x-\hat{x}\right )=0 \Rightarrow f\left ( \hat{x}\right )\leq f\left ( x\right ), \forall x \in S$$
因此,$\hat{x}$ 是全域性最優解。
備註
如果 f 是嚴格偽凸函式,則 $\hat{x}$ 是唯一的全域性最優解。
定理
如果 f 是 S 上的可微偽凸函式,則 f 既是嚴格擬凸函式又是擬凸函式。
備註
在 $\mathbb{R}^n$ 的開集 S 上定義的兩個偽凸函式之和可能不是偽凸函式。
設 $f:S\rightarrow \mathbb{R}$ 是一個擬凸函式,且 S 是 $\mathbb{R}^n$ 的一個非空凸子集,則 f 是偽凸函式當且僅當每個臨界點都是 f 在 S 上的全域性最小值。
設 S 是 $\mathbb{R}^n$ 的一個非空凸子集,且 $f:S\rightarrow \mathbb{R}$ 是一個函式,使得對於每個 $x \in S$,$\bigtriangledown f\left ( x\right )\neq 0$,則 f 是偽凸函式當且僅當它是一個擬凸函式。
凸最佳化 - 規劃問題
凸規劃問題有四種類型:
步驟 1 − $min \:f\left ( x \right )$,其中 $x \in S$,S 是 $\mathbb{R}^n$ 中的一個非空凸集,且 $f\left ( x \right )$ 是凸函式。
步驟 2 − $min \: f\left ( x \right ), x \in \mathbb{R}^n$,受以下約束條件限制:
$g_i\left ( x \right ) \geq 0, 1 \leq m_1$,且 $g_i\left ( x \right )$ 是凸函式。
$g_i\left ( x \right ) \leq 0,m_1+1 \leq m_2$,且 $g_i\left ( x \right )$ 是凹函式。
$g_i\left ( x \right ) = 0, m_2+1 \leq m$,且 $g_i\left ( x \right )$ 是線性函式。
其中 $f\left ( x \right )$ 是凸函式。
步驟 3 − $max \:f\left ( x \right )$,其中 $x \in S$,S 是 $\mathbb{R}^n$ 中的一個非空凸集,且 $f\left ( x \right )$ 是凹函式。
步驟 4 − $min \:f\left ( x \right )$,其中 $x \in \mathbb{R}^n$,受以下約束條件限制:
$g_i\left ( x \right ) \geq 0, 1 \leq m_1$,且 $g_i\left ( x \right )$ 是凸函式。
$g_i\left ( x \right ) \leq 0, m_1+1 \leq m_2$,且 $g_i\left ( x \right )$ 是凹函式。
$g_i\left ( x \right ) = 0,m_2+1 \leq m$,且 $g_i\left ( x \right )$ 是線性函式。
其中 $f\left ( x \right )$ 是凹函式。
可行方向錐
設 S 是 $\mathbb{R}^n$ 中的一個非空集,且設 $\hat{x} \in \:Closure\left ( S \right )$,則 S 在 $\hat{x}$ 處的可行方向錐,記為 D,定義為 $D=\left \{ d:d\neq 0,\hat{x}+\lambda d \in S, \lambda \in \left ( 0, \delta \right ), \delta > 0 \right \}$
每個非零向量 $d \in D$ 稱為可行方向。
對於給定函式 $f:\mathbb{R}^n \Rightarrow \mathbb{R}$,$\hat{x}$ 處的改進方向錐記為 F,且由下式給出:
$$F=\left \{ d:f\left ( \hat{x}+\lambda d \right )\leq f\left ( \hat{x} \right ),\forall \lambda \in \left ( 0,\delta \right ), \delta >0 \right \}$$
每個方向 $d \in F$ 稱為 f 在 $\hat{x}$ 處的改進方向或下降方向。
定理
必要條件
考慮問題 $min f\left ( x \right )$,滿足 $x \in S$,其中 S 是 $\mathbb{R}^n$ 中的非空集。假設 f 在點 $\hat{x} \in S$ 處可微。如果 $\hat{x}$ 是區域性最優解,則 $F_0 \cap D= \phi$,其中 $F_0=\left \{ d:\bigtriangledown f\left ( \hat{x} \right )^T d < 0 \right \}$ 且 D 是可行方向錐。
充分條件
如果 $F_0 \cap D= \phi$,f 是在 $\hat{x}$ 處的偽凸函式,並且存在 $\hat{x}$ 的鄰域 $N_\varepsilon \left ( \hat{x} \right ), \varepsilon > 0$,使得對於任意 $x \in S \cap N_\varepsilon \left ( \hat{x} \right )$,都有 $d=x-\hat{x}\in D$,則 $\hat{x}$ 是區域性最優解。
證明
必要條件
令 $F_0 \cap D\neq \phi$,即存在一個 $d \in F_0 \cap D$,使得 $d \in F_0$ 且 $d\in D$
由於 $d \in D$,因此存在 $\delta_1 >0$,使得 $\hat{x}+\lambda d \in S, \lambda \in \left ( 0,\delta_1 \right ).$
由於 $d \in F_0$,因此 $\bigtriangledown f \left ( \hat{x}\right )^T d <0$
因此,存在 $\delta_2>0$,使得 $f\left ( \hat{x}+\lambda d\right )< f\left ( \hat{x}\right ),\forall \lambda \in f \left ( 0,\delta_2 \right )$
令 $\delta=min \left \{\delta_1,\delta_2 \right \}$
則 $\hat{x}+\lambda d \in S, f\left (\hat{x}+\lambda d \right ) < f\left ( \hat{x} \right ),\forall \lambda \in f \left ( 0,\delta \right )$
但 $\hat{x}$ 是區域性最優解。
因此,這是一個矛盾。
因此 $F_0\cap D=\phi$
充分條件
令 $F_0 \cap D\neq \phi$ 且令 f 為偽凸函式。
令存在 $\hat{x}$ 的鄰域 $N_{\varepsilon}\left ( \hat{x} \right )$,使得 $d=x-\hat{x}, \forall x \in S \cap N_\varepsilon\left ( \hat{x} \right )$
令 $\hat{x}$ 不是區域性最優解。
因此,存在 $\bar{x} \in S \cap N_\varepsilon \left ( \hat{x} \right )$,使得 $f \left ( \bar{x} \right )< f \left ( \hat{x} \right )$
根據 $S \cap N_\varepsilon \left ( \hat{x} \right )$ 的假設,$d=\left ( \bar{x}-\hat{x} \right )\in D$
根據 f 的偽凸性,
$$f\left ( \hat{x} \right )>f\left ( \bar{x} \right )\Rightarrow \bigtriangledown f\left ( \hat{x} \right )^T\left ( \bar{x}-\hat{x} \right )<0$$
$\Rightarrow \bigtriangledown f\left ( \hat{x} \right) ^T d <0$
$\Rightarrow d \in F_0$
因此 $F_0\cap D \neq \phi$
這是矛盾的。
因此,$\hat{x}$ 是區域性最優解。
考慮以下問題:$min \:f\left ( x\right )$,其中 $x \in X$ 滿足 $g_x\left ( x\right ) \leq 0, i=1,2,...,m$
$f:X \rightarrow \mathbb{R},g_i:X \rightarrow \mathbb{R}^n$ 且 X 是 $\mathbb{R}^n$ 中的開集
令 $S=\left \{x:g_i\left ( x\right )\leq 0,\forall i \right \}$
令 $\hat{x} \in X$,則 $M=\left \{1,2,...,m \right \}$
令 $I=\left \{i:g_i\left ( \hat{x}\right )=0, i \in M\right \}$,其中 I 稱為 $\hat{x}$ 處所有活動約束的指標集
令 $J=\left \{i:g_i\left ( \hat{x}\right )<0,i \in M\right \}$,其中 J 稱為 $\hat{x}$ 處所有非活動約束的指標集。
令 $F_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown f\left ( \hat{x} \right )^T d <0 \right \}$
令 $G_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown gI\left ( \hat{x} \right )^T d <0 \right \}$
或 $G_0=\left \{ d \in \mathbb{R}^m:\bigtriangledown gi\left ( \hat{x} \right )^T d <0 ,\forall i \in I \right \}$
引理
如果 $S=\left \{ x \in X:g_i\left ( x\right ) \leq 0, \forall i \in I\right \}$ 且 X 是 $\mathbb{R}^n$ 中的非空開集。令 $\hat{x}\in S$ 且 $g_i$ 在 $\hat{x}, i \in I$ 處可微,且 $g_i$ 在 $\hat{x}$ 處連續,其中 $i \in J$,則 $G_0 \subseteq D$。
證明
令 $d \in G_0$
由於 $\hat{x} \in X$ 且 X 是開集,因此存在 $\delta_1 >0$,使得對於 $\lambda \in \left ( 0, \delta_1\right )$,都有 $\hat{x}+\lambda d \in X$
同樣,由於 $g_\hat{x}<0$ 且 $g_i$ 在 $\hat{x}, \forall i \in J$ 處連續,因此存在 $\delta_2>0$,使得 $g_i\left ( \hat{x}+\lambda d\right )<0, \lambda \in \left ( 0, \delta_2\right )$
由於 $d \in G_0$,因此,$\bigtriangledown g_i\left ( \hat{x}\right )^T d <0, \forall i \in I$,因此存在 $\delta_3 >0, g_i\left ( \hat{x}+\lambda d\right )< g_i\left ( \hat{x}\right )=0$,對於 $\lambda \in \left ( 0, \delta_3\right ) i \in J$
令 $\delta=min\left \{ \delta_1, \delta_2, \delta_3 \right \}$
因此,$\hat{x}+\lambda d \in X, g_i\left ( \hat{x}+\lambda d\right )< 0, i \in M$
$\Rightarrow \hat{x}+\lambda d \in S$
$\Rightarrow d \in D$
$\Rightarrow G_0 \subseteq D$
因此得證。
定理
必要條件
令 f 和 $g_i, i \in I$ 在 $\hat{x} \in S$ 處可微,且 $g_j$ 在 $\hat{x} \in S$ 處連續。如果 $\hat{x}$ 是 S 的區域性極小值點,則 $F_0 \cap G_0=\phi$。
充分條件
如果 $F_0 \cap G_0= \phi$ 且 f 是在 $\left (\hat{x}, g_i 9x \right ), i \in I$ 處的偽凸函式,且 $g_i$ 是在 $\hat{x}$ 的某個 $\varepsilon$ -鄰域上嚴格偽凸函式,則 $\hat{x}$ 是區域性最優解。
備註
令 $\hat{x}$ 為一個可行點,使得 $\bigtriangledown f\left(\hat{x} \right)=0$,則 $F_0 = \phi$。因此,$F_0 \cap G_0= \phi$,但 $\hat{x}$ 不是最優解
但如果 $\bigtriangledown g\left(\hat{x} \right)=0$,則 $G_0=\phi$,因此 $F_0 \cap G_0= \phi$
考慮問題:min $f\left(x \right)$ 滿足 $g\left(x \right)=0$。
由於 $g\left(x \right)=0$,因此 $g_1\left(x \right)=g\left(x \right)<0$ 且 $g_2\left(x \right)=-g\left(x \right) \leq 0$。
令 $\hat{x} \in S$,則 $g_1\left(\hat{x} \right)=0$ 且 $g_2\left(\hat{x} \right)=0$。
但 $\bigtriangledown g_1\left(\hat{x} \right)= - \bigtriangledown g_2\left(\hat{x}\right)$
因此,$G_0= \phi$ 且 $F_0 \cap G_0= \phi$。
凸最佳化 - Fritz-John 條件
必要條件
定理
考慮問題 − $min f\left ( x \right )$,滿足 $x \in X$,其中 X 是 $\mathbb{R}^n$ 中的開集,且令 $g_i \left ( x \right ) \leq 0, \forall i =1,2,....m$。
令 $f:X \rightarrow \mathbb{R}$ 且 $g_i:X \rightarrow \mathbb{R}$
令 $\hat{x}$ 為可行解,且令 f 和 $g_i, i \in I$ 在 $\hat{x}$ 處可微,且 $g_i, i \in J$ 在 $\hat{x}$ 處連續。
如果 $\hat{x}$ 在區域性上解決了上述問題,則存在 $u_0, u_i \in \mathbb{R}, i \in I$,使得 $u_0 \bigtriangledown f\left ( \hat{x} \right )+\displaystyle\sum\limits_{i\in I} u_i \bigtriangledown g_i \left ( \hat{x} \right )$=0
其中 $u_0,u_i \geq 0,i \in I$ 且 $\left ( u_0, u_I \right ) \neq \left ( 0,0 \right )$
此外,如果 $g_i,i \in J$ 在 $\hat{x}$ 處也可微,則上述條件可以寫成 −
$u_0 \bigtriangledown f\left ( \hat{x}\right )+\displaystyle\sum\limits_{i=1}^m u_i \bigtriangledown g_i\left ( \hat{x} \right )=0$
$u_ig_i\left (\hat{x} \right )$=0
$u_0,u_i \geq 0, \forall i=1,2,....,m$
$\left (u_0,u \right ) \neq \left ( 0,0 \right ), u=\left ( u_1,u_2,s,u_m \right ) \in \mathbb{R}^m$
備註
$u_i$ 稱為拉格朗日乘子。
$\hat{x}$ 滿足給定問題的可行性條件稱為原始可行性條件。
要求 $u_0 \bigtriangledown f\left (\hat{x} \right )+\displaystyle\sum\limits_{i=1}^m u-i \bigtriangledown g_i\left ( x \right )=0$ 稱為對偶可行性條件。
條件 $u_ig_i\left ( \hat{x} \right )=0, i=1, 2, ...m$ 稱為互補鬆弛條件。此條件要求 $u_i=0, i \in J$
原始可行性條件、對偶可行性條件和互補鬆弛條件一起稱為 Fritz-John 條件。
充分條件
定理
如果存在 $\hat{x}$ 的 $\varepsilon$-鄰域 $N_\varepsilon \left ( \hat{x} \right ),\varepsilon >0$,使得 f 在 $N_\varepsilon \left ( \hat{x} \right )\cap S$ 上是偽凸的,且 $g_i,i \in I$ 在 $N_\varepsilon \left ( \hat{x}\right )\cap S$ 上是嚴格偽凸的,則 $\hat{x}$ 是上述問題的一個區域性最優解。如果 f 在 $\hat{x}$ 處是偽凸的,且如果 $g_i, i \in I$ 在 $\hat{x}$ 處既是嚴格偽凸函式又是擬凸函式,則 $\hat{x}$ 是上述問題的一個全域性最優解。
示例
$min \:f\left ( x_1,x_2 \right )=\left ( x_1-3 \right )^2+\left ( x_2-2 \right )^2$
滿足 $x_{1}^{2}+x_{2}^{2} \leq 5, x_1+2x_2 \leq 4, x_1,x_2 \geq 0$ 且 $\hat{x}=\left ( 2,1 \right )$
令 $g_1\left (x_1,x_2 \right )=x_{1}^{2}+x_{2}^{2} -5,$
$g_2\left (x_1,x_2 \right )=x_1+2x_2-4,$
$g_3\left (x_1,x_2 \right )=-x_1$ 且 $g_4\left ( x_1, x_2 \right )= -x_2$。
因此,上述約束可以寫成 −
$g_1\left (x_1,x_2 \right )\leq 0,$
$g_2\left (x_1,x_2 \right )\leq 0,$
$g_3\left (x_1,x_2 \right )\leq 0$ 且
$g_4\left (x_1,x_2 \right )\leq 0$ 因此,$I = \left \{1,2 \right \}$,因此,$u_3=0,u_4=0$
$\bigtriangledown f \left (\hat{x} \right )=\left (2,-2 \right ),\bigtriangledown g_1\left (\hat{x} \right )=\left (4,2 \right )$ 且 $\bigtriangledown g_2\left (\hat{x} \right )=\left (1,2 \right )$
因此,將這些值代入 Fritz-John 條件的第一條件,得到 −
$u_0=\frac{3}{2} u_2, \:\:u_1= \frac{1}{2}u_2,$ 且令 $u_2=1$,因此 $u_0= \frac{3}{2},\:\:u_1= \frac{1}{2}$
因此,Fritz John 條件得到滿足。
$min f\left (x_1,x_2\right )=-x_1$。
滿足 $x_2-\left (1-x_1\right )^3 \leq 0$,
$-x_2 \leq 0$ 且 $\hat{x}=\left (1,0\right )$
令 $g_1\left (x_1,x_2 \right )=x_2-\left (1-x_1\right )^3$,
$g_2\left (x_1,x_2 \right )=-x_2$
因此,上述約束可以寫成 −
$g_1\left (x_1,x_2 \right )\leq 0,$
$g_2\left (x_1,x_2 \right )\leq 0,$
因此,$I=\left \{1,2 \right \}$
$\bigtriangledown f\left (\hat{x} \right )=\left (-1,0\right )$
$\bigtriangledown g_1 \left (\hat{x} \right )=\left (0,1\right )$ 且 $g_2 \left (\hat{x} \right )=\left (0, -1 \right )$
因此,將這些值代入 Fritz-John 條件的第一條件,得到 −
$u_0=0,\:\: u_1=u_2=a>0$
因此,Fritz John 條件得到滿足。
Karush-Kuhn-Tucker最優性必要條件
考慮問題 −
$min \:f\left ( x \right )$ 滿足 $x \in X$,其中 X 是 $\mathbb{R}^n$ 中的開集,且 $g_i \left ( x \right )\leq 0, i=1, 2,...,m$
令 $S=\left \{ x \in X:g_i\left ( x \right )\leq 0, \forall i \right \}$
令 $\hat{x} \in S$,且令 f 和 $g_i,i \in I$ 在 $\hat{x}$ 處可微,且 $g_i, i \in J$ 在 $\hat{x}$ 處連續。此外,$\bigtriangledown g_i\left ( \hat{x} \right), i \in I$ 線性無關。如果 $\hat{x}$ 在區域性上解決了上述問題,則存在 $u_i,i \in I$,使得
$\bigtriangledown f\left ( x\right)+\displaystyle\sum\limits_{i\in I} u_i \bigtriangledown g_i\left ( \hat{x} \right)=0$, $\:\:u_i \geq 0, i \in I$
如果 $g_i,i \in J$ 在 $\hat{x}$ 處也可微,則
$\bigtriangledown f\left ( \hat{x}\right)+\displaystyle\sum\limits_{i= 1}^m u_i \bigtriangledown g_i\left ( \hat{x} \right)=0$
$u_ig_i\left ( \hat{x} \right)=0, \forall i=1,2,...,m$
$u_i \geq 0 \forall i=1,2,...,m$
示例
考慮以下問題 -
$min \:f\left ( x_1,x_2 \right )=\left ( x_1-3\right )^2+\left ( x_2-2\right )^2$
使得 $x_{1}^{2}+x_{2}^{2}\leq 5$,
$x_1,2x_2 \geq 0$ 且 $\hat{x}=\left ( 2,1 \right )$
令 $g_1\left ( x_1, x_2 \right)=x_{1}^{2}+x_{2}^{2}-5$,
$g_2\left ( x_1, x_2 \right)=x_{1}+2x_2-4$
$g_3\left ( x_1, x_2 \right)=-x_{1}$ 且 $g_4\left ( x_1,x_2 \right )=-x_2$
因此,上述約束可以寫成 −
$g_1 \left ( x_1,x_2 \right)\leq 0, g_2 \left ( x_1,x_2 \right) \leq 0$
$g_3 \left ( x_1,x_2 \right)\leq 0,$ 且 $g_4 \left ( x_1,x_2 \right) \leq 0$ 因此,$I=\left \{ 1,2 \right \}$,所以, $ u_3=0,\:\: u_4=0$
$\bigtriangledown f \left ( \hat{x} \right)=\left ( 2,-2 \right), \bigtriangledown g_1 \left ( \hat{x} \right)= \left ( 4,2 \right)$ 且
$\bigtriangledown g_2\left ( \hat{x} \right ) =\left ( 1,2 \right )$
因此,將這些值代入 Karush-Kuhn-Tucker 條件的第一條件,得到 -
$u_1=\frac{1}{3}$ 且 $u_2=\frac{2}{3}$
因此,Karush-Kuhn-Tucker 條件滿足。
凸問題的演算法
最速下降法
此方法也稱為梯度法或柯西法。此方法涉及以下術語 -
$$x_{k+1}=x_k+\alpha_kd_k$$
$d_k= - \bigtriangledown f\left ( x_k \right )$ 或 $ d_k= -\frac{\bigtriangledown f\left ( x_k \right )}{\left \| \bigtriangledown f\left ( x_k \right ) \right \|}$
令 $\phi \left (\alpha \right )=f\left ( x_k +\alpha d_k\right )$
透過對 $\phi$ 求導並使其等於零,我們可以得到 $\alpha$。
因此,演算法如下 -
初始化 $x_0$,$\varepsilon_1$,$\varepsilon_2$ 並設定 $k=0$。
設定 $d_k=-\bigtriangledown f\left ( x_k \right ) $或 $d_k=-\frac{\bigtriangledown f\left (x_k \right )}{\left \|\bigtriangledown f\left (x_k \right ) \right \|}$。
找到 $\alpha_k$ 使其最小化 $\phi\left ( \alpha \right )=f\left ( x_k+\alpha d_k \right )$。
設定 $x_{k+1}=x_k+\alpha_kd_k$。
如果 $\left \| x_{k+1-x_k} \right \| <\varepsilon_1$ 或 $\left \| \bigtriangledown f\left ( x_{k+1} \right ) \right \| \leq \varepsilon_2$,則轉到步驟 6,否則設定 $k=k+1$ 並轉到步驟 2。
最優解為 $\hat{x}=x_{k+1}$。
牛頓法
牛頓法基於以下原理 -
$f\left ( x \right )=y\left ( x \right )=f\left ( x_k \right )+\left ( x-x_k \right )^T \bigtriangledown f\left ( x_k \right )+\frac{1}{2}\left ( x-x_k \right )^T H\left ( x_k \right )\left ( x-x_k \right )$
$\bigtriangledown y\left ( x \right )=\bigtriangledown f\left ( x_k \right )+H\left ( x_k \right )\left ( x-x_k \right )$
在 $x_{k+1}$ 處,$\bigtriangledown y\left ( x_{k+1} \right )=\bigtriangledown f\left ( x_k \right )+H\left ( x_k \right )\left ( x_{k+1}-x_k \right )$
為了使 $x_{k+1}$ 為最優解,$\bigtriangledown y\left ( x_k+1 \right )=0$
因此,$x_{k+1}=x_k-H\left ( x_k \right )^{-1} \bigtriangledown f\left ( x_k \right )$
這裡 $H\left ( x_k \right )$ 應為非奇異的。
因此,演算法如下 -
步驟 1 - 初始化 $x_0$,$\varepsilon$ 並設定 $k=0$。
步驟 2 - 找到 $H\left ( x_k \right ) \bigtriangledown f\left ( x_k \right )$。
步驟 3 - 求解線性系統 $H\left ( x_k \right )h\left ( x_k \right )=\bigtriangledown f\left ( x_k \right )$ 以獲得 $h\left ( x_k \right )$。
步驟 4 - 找到 $x_{k+1}=x_k-h\left ( x_k \right )$。
步驟 5 - 如果 $\left \| x_{k+1}-x_k \right \|< \varepsilon$ 或 $\left \| \bigtriangledown f\left ( x_k \right ) \right \| \leq \varepsilon$,則轉到步驟 6,否則設定 $k=k+1$ 並轉到步驟 2。
步驟 6 - 最優解為 $\hat{x}=x_{k+1}$。
共軛梯度法
此方法用於解決以下型別的問題 -
$min f\left ( x \right )=\frac{1}{2}x^T Qx-bx$
其中 Q 是一個正定 nXn 矩陣,b 是常數。
給定 $x_0$,$\varepsilon$,計算 $g_0=Qx_0-b$
設定 $d_0=-g_0$,對於 $k=0,1,2,...,$
設定 $\alpha_k=\frac{g_{k}^{T}g_k}{d_{k}^{T}Q d_k}$
計算 $x_{k+1}=x_k+\alpha_kd_k$
設定 $g_{k+1}=g_k+\alpha_kd_k$
計算 $\beta_k=\frac{g_{k}^{T}g_k}{d_{k}^{T}Qd_k}$
計算 $x_{k+1}=x_k+\alpha_kd_k$
設定 $g_{k+1}=x_k+\alpha_kQd_k$
計算 $\beta_k=\frac{g_{k+1}^{T}g_{k+1}}{g_{k}^{T}gk}$
設定 $d_{k+1}=-g_{k+1}+\beta_kd_k$。