凸最佳化 - 線性規劃

---

---

方法論

線性規劃，也稱為線性最佳化，是一種用於解決數學問題的方法，其中關係本質上是線性的。線性規劃的基本性質是最大化或最小化一個**目標函式**，並受一些**約束**條件的限制。目標函式是一個線性函式，它是從問題的數學模型中獲得的。約束條件是強加於模型上的條件，並且也是線性的。

• 從給定的問題中，找出目標函式。
• 找到約束條件。
• 在圖上繪製約束條件。
• 找到可行域，它是所有約束條件的交集。
• 找到可行域的頂點。
• 找到目標函式在這些頂點處的取值。
• 哪個頂點使得目標函式最大化或最小化（根據問題而定）就是答案。

示例

**步驟 1** - 在以下約束條件下最大化 $5x+3y$

$x+y\leq 2$，

$3x+y\leq 3$，

$x\geq 0 \:和 \:y\geq 0$

**解** -

第一步是在圖上找到可行域。

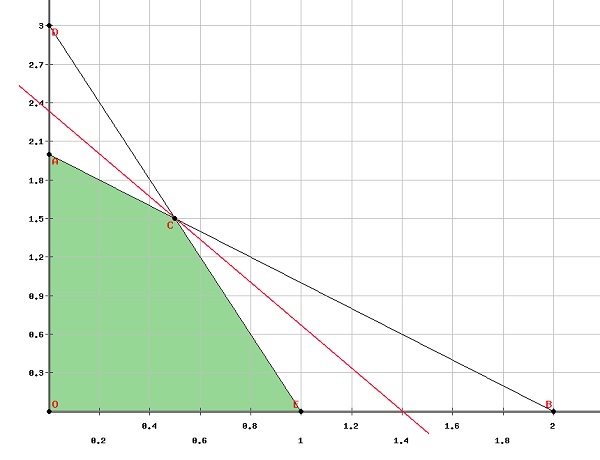
從圖中可以清楚地看出，可行域的頂點是

$\left ( 0, 0 \right )\left ( 0, 2 \right )\left ( 1, 0 \right )\left ( \frac{1}{2}, \frac{3}{2} \right )$

令 $f\left ( x, y \right )=5x+3y$

將這些值代入目標函式，我們得到 -

$f\left ( 0, 0 \right )$=0

$f\left ( 0, 2 \right )$=6

$f\left ( 1, 0 \right )$=5

$f\left ( \frac{1}{2}, \frac{3}{2} \right )$=7

因此，函式在 $\left ( \frac{1}{2}, \frac{3}{2} \right )$ 處取得最大值。

**步驟 2** - 一家手錶公司生產電子錶和機械錶。長期預測表明，每天至少需要 100 塊電子錶和 80 塊機械錶的需求。由於生產能力的限制，每天最多隻能生產 200 塊電子錶和 170 塊機械錶。為了滿足運輸合同，每天必須運送至少 200 塊手錶。

如果每售出一塊電子錶就會損失 2 美元，但每售出一塊機械錶就會獲得 5 美元的利潤，那麼每天應該生產多少塊每種手錶才能最大化淨利潤？

**解** -

令 $x$ 為生產的電子錶數量

$y$ 為生產的機械錶數量

根據題意，每天至少要生產 100 塊電子錶，最多生產 200 塊電子錶。

$\Rightarrow 100 \leq \:x\leq 200$

類似地，每天至少要生產 80 塊機械錶，最多生產 170 塊機械錶。

$\Rightarrow 80 \leq \:y\leq 170$

由於每天至少要生產 200 塊手錶。

$\Rightarrow x +y\leq 200$

由於每售出一塊電子錶就會損失 2 美元，但每售出一塊機械錶就會獲得 5 美元的利潤，

總利潤可以計算為

$利潤 =-2x + 5y$

我們需要最大化利潤，因此，這個問題可以表述為 -

在以下約束條件下最大化 $-2x + 5y$

$100 \:\leq x\:\leq 200$

$80 \:\leq y\:\leq 170$

$x+y\:\leq 200$

將上述方程在圖上繪製出來，我們得到，

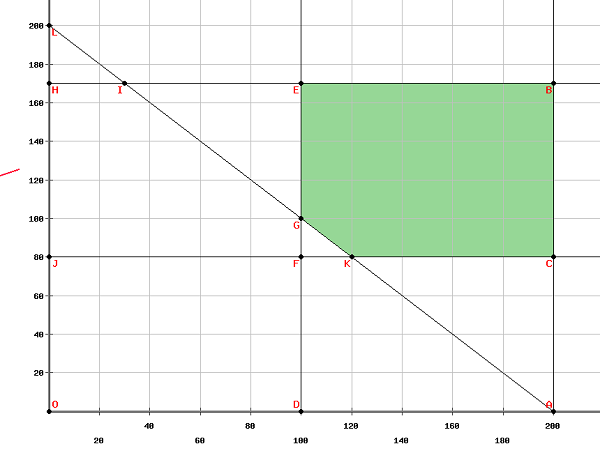
可行域的頂點是

$\left ( 100, 170\right )\left ( 200, 170\right )\left ( 200, 180\right )\left ( 120, 80\right ) 和 \left ( 100, 100\right )$

目標函式的最大值在 $\left ( 100, 170\right )$ 處取得。因此，為了最大化淨利潤，應該生產 100 塊電子錶和 170 塊機械錶。