凸最佳化 - 極小值和極大值

區域性極小值或極小點

如果$\forall x \in N_\varepsilon \left ( \bar{x} \right )$，$f\left ( \bar{x} \right )\leq f\left ( x \right )$，則稱$\bar{x}\in \:S$為函式$f$的區域性極小點，其中$N_\varepsilon \left ( \bar{x} \right )$表示$\bar{x}$的鄰域，即$N_\varepsilon \left ( \bar{x} \right )$表示$\left \| x-\bar{x} \right \|< \varepsilon$

區域性極大值或極大點

如果$\forall x \in N_\varepsilon \left ( \bar{x} \right )$，$f\left ( \bar{x} \right )\geq f\left ( x \right )$，則稱$\bar{x}\in \:S$為函式$f$的區域性極大點，其中$N_\varepsilon \left ( \bar{x} \right )$表示$\bar{x}$的鄰域，即$N_\varepsilon \left ( \bar{x} \right )$表示$\left \| x-\bar{x} \right \|< \varepsilon$

全域性極小值

如果$\forall x \in S$，$f\left ( \bar{x} \right )\leq f\left ( x \right )$，則稱$\bar{x}\in \:S$為函式$f$的全域性極小點

全域性極大值

如果$\forall x \in S$，$f\left ( \bar{x} \right )\geq f\left ( x \right )$，則稱$\bar{x}\in \:S$為函式$f$的全域性極大點

示例

步驟1 - 求函式$f\left ( \bar{x} \right )=\left | x^2-4 \right |$的區域性極小值和區域性極大值

解 -

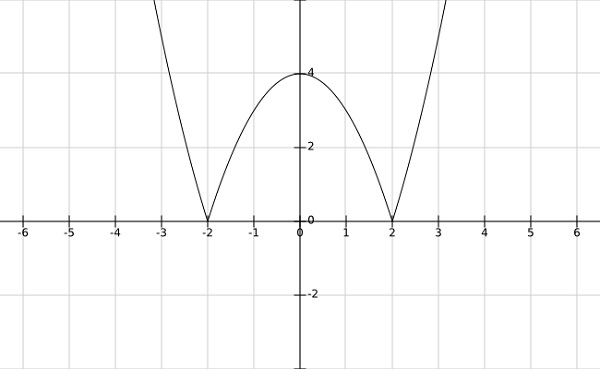
從上圖可以看出，區域性極小值出現在$x= \pm 2$，區域性極大值出現在$x = 0$

步驟2 - 求函式$f\left (x \right )=\left | 4x^3-3x^2+7 \right |$的全域性極小值

解 -

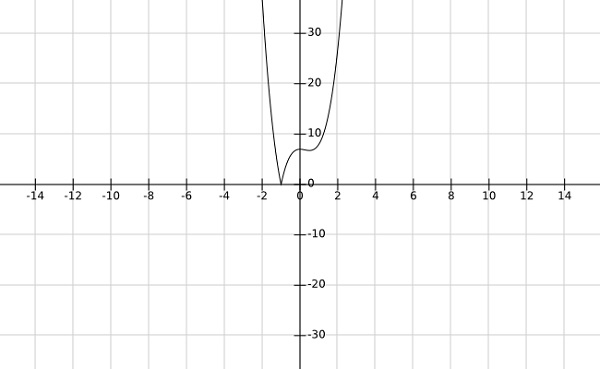
從上圖可以看出，全域性極小值出現在$x=-1$。