
模擬通訊 - 殘留邊帶抑制載波調製
在之前的章節中,我們討論了SSBSC調製和解調。SSBSC調製訊號只有一個邊帶頻率。理論上,我們可以使用理想的帶通濾波器完全獲得一個邊帶頻率分量。然而,實際上我們可能無法獲得整個邊帶頻率分量。由於這個原因,一些資訊會丟失。
為了避免這種損失,選擇了一種介於DSBSC和SSBSC之間的技術。這種技術被稱為**殘留邊帶抑制載波(VSBSC)**技術。“殘留”一詞意為“一部分”,名稱由此而來。
**VSBSC調製**是一種過程,其中一部分訊號(稱為殘留)與一個邊帶一起被調製。VSBSC波的頻譜如下圖所示。
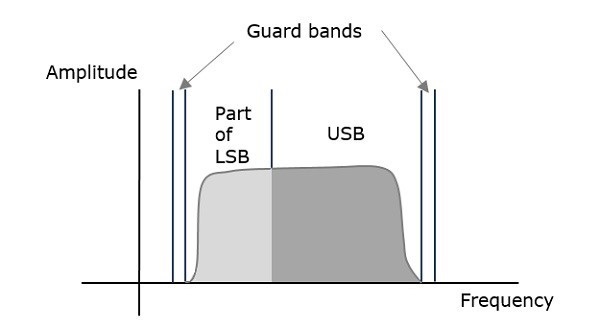
除了上邊帶,這種技術還會傳輸一部分下邊帶。類似地,我們可以傳輸下邊帶以及一部分上邊帶。為了避免干擾,在VSB的兩側都設定了一個非常小的保護帶。VSB調製主要用於電視傳輸。
VSBSC調製的頻寬
我們知道SSBSC調製波的頻寬為$f_m$。由於VSBSC調製波包含一個邊帶的頻率分量以及另一個邊帶的殘留分量,因此其頻寬將是SSBSC調製波頻寬和殘留頻率$f_v$之和。
即,VSBSC調製波的頻寬 = $f_m + f_v$
優點
以下是VSBSC調製的優點。
效率高。
與AM和DSBSC波相比,頻寬減小。
濾波器設計簡單,不需要高精度。
可以輕鬆傳輸低頻分量。
具有良好的相位特性。
缺點
以下是VSBSC調製的缺點。
與SSBSC波相比,頻寬更大。
解調複雜。
應用
VSBSC最突出和標準的應用是電視訊號的傳輸。此外,在考慮頻寬使用率時,這也是最方便和最有效率的技術。
現在,讓我們分別討論一下產生VSBSC波的調製器和解調VSBSC波的解調器。
VSBSC的產生
VSBSC波的產生類似於SSBSC波的產生。VSBSC調製器如下圖所示。
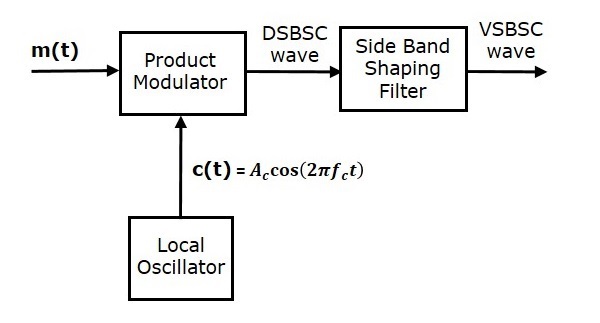
在這種方法中,我們首先將使用乘法調製器產生DSBSC波。然後,將此DSBSC波作為邊帶整形濾波器的輸入。該濾波器產生一個輸出,即VSBSC波。
調製訊號$m\left ( t \right )$和載波訊號$A_c \cos \left ( 2 \pi f_ct \right )$作為輸入應用於乘法調製器。因此,乘法調製器產生的輸出是這兩個輸入的乘積。
因此,乘法調製器的輸出為
$$p\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )m\left ( t \right )$$
對兩邊應用傅立葉變換
$$P\left ( f \right )=\frac{A_c}{2}\left [ M\left ( f-f_c \right )+M\left ( f+f_c \right ) \right ]$$
上述方程表示DSBSC頻譜方程。
設邊帶整形濾波器的傳遞函式為$H\left ( f \right )$。該濾波器的輸入為$p\left ( t \right )$,輸出為VSBSC調製波$s\left ( t \right )$。$p\left ( t \right )$和$s\left ( t \right )$的傅立葉變換分別為$P\left ( t \right )$和$S\left ( t \right )$。
數學上,我們可以將$S\left ( f \right )$寫成
$$S\left ( t \right )=P\left ( f \right )H\left ( f \right )$$
將$P\left ( f \right )$的值代入上式。
$$S\left ( f \right )=\frac{A_c}{2}\left [ M\left ( f-f_c \right )+M\left ( f+f_c \right ) \right ]H\left ( f \right )$$
上述方程表示VSBSC頻譜方程。
VSBSC的解調
VSBSC波的解調類似於SSBSC波的解調。這裡,使用相同的載波訊號(用於產生VSBSC波)來檢測訊息訊號。因此,這個檢測過程被稱為**相干**或**同步檢測**。VSBSC解調器如下圖所示。
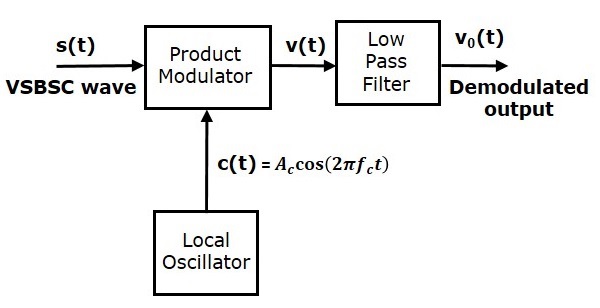
在這個過程中,可以透過將VSBSC波與具有與VSBSC調製中使用的載波相同頻率和相位的載波相乘來提取訊息訊號。然後將所得訊號透過低通濾波器。該濾波器的輸出是所需的訊息訊號。
設VSBSC波為$s\left ( t \right )$,載波訊號為$A_c \cos \left ( 2 \pi f_ct \right )。
從圖中,我們可以將乘法調製器的輸出寫成
$$v\left ( t \right )= A_c \cos\left ( 2 \pi f_ct \right )s\left ( t \right )$$
對兩邊應用傅立葉變換
$$V\left ( f \right )= \frac{A_c}{2}\left [ S\left ( f-f_c \right )+S\left ( f+f_c \right ) \right ]$$
我們知道$S\left ( f \right )=\frac{A_c}{2}\left [ M\left ( f-f_c \right ) + M\left ( f+f_c \right )\right ]H\left ( f \right )$
從上式,讓我們求出$S\left ( f-f_c \right )$和$S\left ( f+f_c \right )。
$$S\left ( f-f_c \right )=\frac{A_c}{2}\left [ M\left ( f-f_c-f_c \right ) + M\left ( f-f_c+f_c \right )\right ]H\left ( f-f_c \right )$$
$\Rightarrow S\left ( f-f_c \right )=\frac{A_c}{2}\left [ M\left ( f-2f_c \right )+M\left ( f \right ) \right ] H\left ( f-f_c \right )$
$$S\left ( f+f_c \right )=\frac{A_c}{2}\left [ M\left ( f+f_c-f_c \right ) +M\left ( f+f_c+f_c \right )\right ] H\left ( f+f_c \right )$$
$\Rightarrow S\left ( f+f_c \right )=\frac{A_c}{2}\left [ M \left ( f \right )+M \left (f+2f_c \right ) \right ] H \left ( f+f_c \right )$
將$S\left ( f-f_c \right )$和$S\left ( f+f_c \right )$的值代入$V\left ( f \right )。
$V(f) = \frac{A_c}{2}[\frac{A_c}{2}[M(f-2f_c)+M(f)]H(f-f_c)+$
$\frac{A_c}{2}[M(f)+M(f+2f_c)]H(f+f_c)]$
$\Rightarrow V\left ( f \right )=\frac{{A_{c}}^{2}}{4} M\left ( f \right )\left [ H\left ( f-f_c \right )+H \left ( f+f_c \right ) \right ]$
$+ \frac{{A_{c}}^{2}}{4}\left [ M\left ( f-2f_c \right )H\left ( f-f_c \right )+M\left ( f+2f_c \right )H\left ( f+f_c \right ) \right ]$
在上式中,第一項表示所需訊息訊號頻譜的縮放版本。可以透過將上述訊號透過低通濾波器來提取它。
$$V_0\left ( f \right )=\frac{{A_{c}}^{2}}{4} M\left ( f \right )\left [ H\left ( f-f_c \right )+H\left ( f+f_c \right ) \right ]$$