
模擬通訊 - 快速指南
模擬通訊 - 緒論
“通訊”一詞源於拉丁語 commūnicāre,意為“分享”。通訊是資訊交換的基本步驟。
例如,嬰兒在搖籃裡,當需要母親時會透過哭聲進行交流。牛遇到危險時會大聲哞叫。人藉助語言進行交流。溝通是分享的橋樑。
通訊可以定義為透過諸如文字、行動、符號等方式在兩個或兩個以上個體之間交換資訊的過程。
通訊系統組成部分
任何提供通訊的系統都包含三個重要的基本部分,如下圖所示。
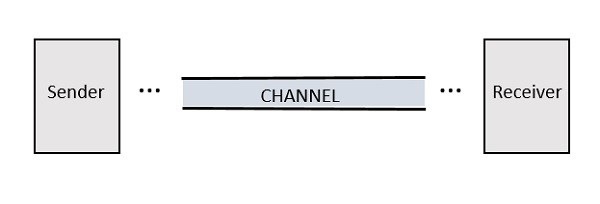
傳送方是傳送訊息的人。它可以是訊號從其傳送的發射站。
通道是訊息訊號傳輸到達目的地的媒介。
接收方是接收訊息的人。它可以是接收傳輸訊號的接收站。
訊號型別
透過手勢、聲音、動作等方式傳遞資訊可以稱為訊號。因此,訊號可以是傳輸某些資訊的能量源。此訊號有助於在傳送方和接收方之間建立通訊。
在通訊系統中,傳輸一定距離以傳送訊息的電脈衝或電磁波可以稱為訊號。
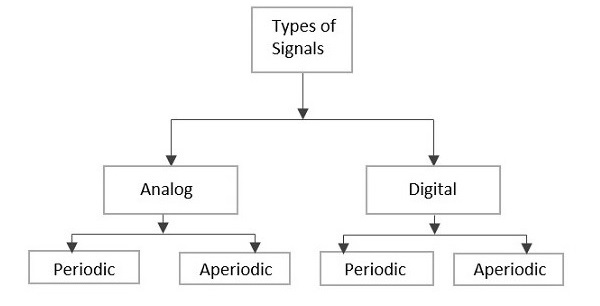
根據其特性,訊號主要分為兩種型別:模擬和數字。模擬和數字訊號進一步分類,如下圖所示。
模擬訊號
表示時間變化量的連續時間變化訊號可以稱為模擬訊號。此訊號隨時間變化而持續變化,根據表示它的量的瞬時值。
示例
讓我們考慮一個水龍頭,它在一個小時內(早上 6 點到 7 點)充滿一個 100 升容量的水箱。填充水箱的部分由變化的時間決定。這意味著,15 分鐘後(早上 6:15),水箱的四分之一被填滿,而在早上 6:45,水箱的 3/4 被填滿。
如果我們嘗試根據變化的時間繪製水箱中水量的變化部分,它將類似於下圖。
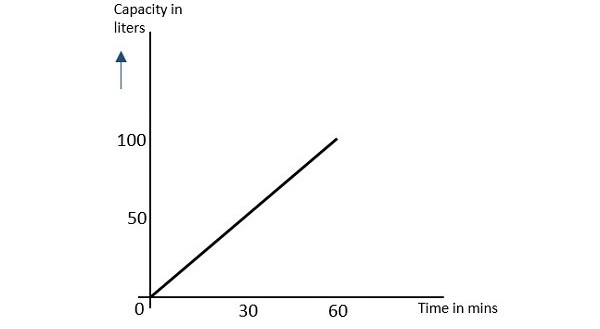
由於此影像中顯示的結果根據時間變化(增加),因此此時間變化量可以理解為模擬量。圖中用傾斜線表示此條件的訊號是模擬訊號。基於模擬訊號和模擬值的通訊稱為模擬通訊。
數字訊號
本質上是離散的或形式上不連續的訊號可以稱為數字訊號。此訊號具有單獨表示的個體值,不基於先前值,就像它們是在特定時間點派生的一樣。
示例
讓我們考慮一個有 20 名學生的教室。如果繪製他們一週的出勤情況,它將類似於下圖。
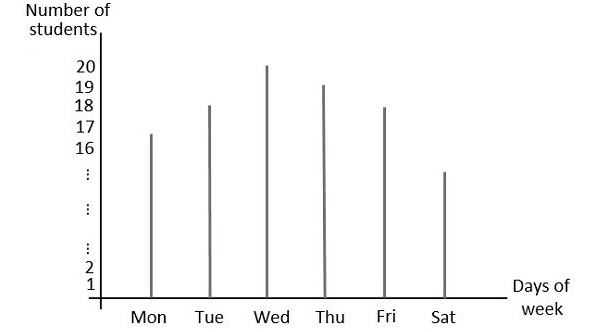
在此圖中,值是單獨陳述的。例如,星期三的課堂出勤率為 20,而星期六為 15。這些值可以分別或離散地單獨考慮,因此它們被稱為離散值。
只有 1 和 0 的二進位制數字大多稱為數字值。因此,表示 1 和 0 的訊號也稱為數字訊號。基於數字訊號和數字值的通訊稱為數字通訊。
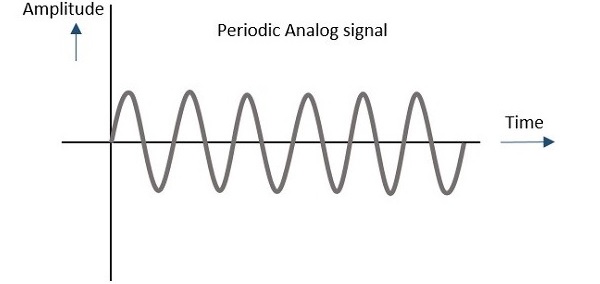
週期訊號
任何在一段時間內重複其模式的模擬或數字訊號都稱為週期訊號。此訊號的模式重複持續,並且易於假設或計算。
示例
如果我們考慮工業中的機器,則一個接一個發生的流程是一個連續的過程。例如,採購和分揀原材料、分批加工材料、一個接一個地包裝一批產品等,重複遵循一定的程式。
無論考慮模擬還是數字,此類過程都可以用圖形表示如下。
非週期訊號
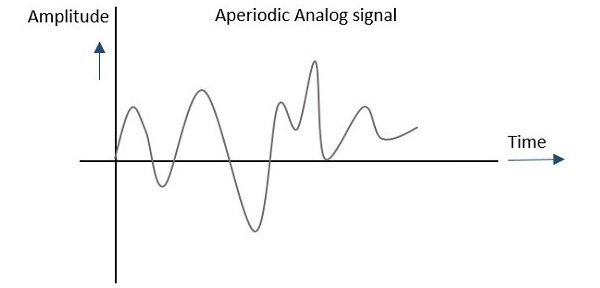
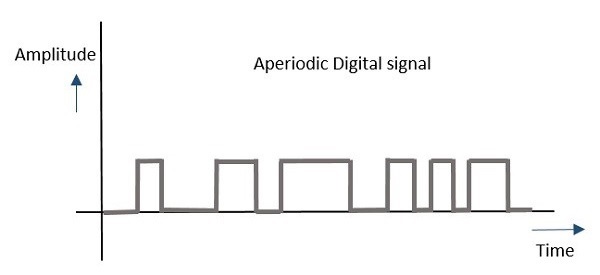
任何在一段時間內不重複其模式的模擬或數字訊號都稱為非週期訊號。此訊號的模式持續,但模式不重複。它也不容易假設或計算。
示例
如果考慮一個人的日常生活,則包括各種型別的活動,這些活動需要不同時間段來完成不同的任務。時間間隔或工作不會持續重複。例如,一個人不會從早到晚持續刷牙,而且時間間隔也相同。
無論考慮模擬還是數字,此類過程都可以用圖形表示如下。
通常,通訊系統中使用的訊號本質上是模擬的,根據需要以模擬方式傳輸或轉換為數字然後傳輸。
模擬通訊 - 調製
為了將訊號傳輸到一定距離,不受任何外部干擾或噪聲新增的影響,並且不會衰減,它必須經歷一個稱為調製的過程。它可以增強訊號強度,而不會干擾原始訊號的引數。
什麼是調製?
攜帶訊息的訊號必須傳輸一定距離,並且為了建立可靠的通訊,它需要藉助高頻訊號,該訊號不應影響訊息訊號的原始特性。
如果訊息訊號的特性發生變化,則其中包含的訊息也會發生改變。因此,必須注意訊息訊號。高頻訊號可以傳輸到更遠的距離,而不會受到外部干擾的影響。我們藉助這種稱為載波訊號的高頻訊號來傳輸我們的訊息訊號。這樣的過程簡單地稱為調製。
調製是根據調製訊號的瞬時值改變載波訊號引數的過程。
調製的必要性
基帶訊號不適合直接傳輸。對於此類訊號,要傳輸更長的距離,必須透過與不影響調製訊號引數的高頻載波進行調製來增強其強度。
調製的優點
如果沒有引入調製,用於傳輸的天線必須非常大。通訊範圍會受到限制,因為波無法在沒有失真的情況下傳輸一定距離。
以下是通訊系統中實施調製的一些優點。
- 減少天線尺寸
- 無訊號混合
- 增加通訊範圍
- 訊號多路複用
- 頻寬調整的可能性
- 改善接收質量
調製過程中的訊號
以下是調製過程中的三種訊號型別。
訊息或調製訊號
包含要傳輸訊息的訊號稱為訊息訊號。它是基帶訊號,必須經過調製過程才能傳輸。因此,它也稱為調製訊號。
載波訊號
具有特定幅度、頻率和相位但不包含資訊的諧波高頻訊號稱為載波訊號。它是一個空訊號,用於在調製後將訊號傳輸到接收器。
調製訊號
調製過程後的結果訊號稱為調製訊號。此訊號是調製訊號和載波訊號的組合。
調製型別
有許多型別的調製。根據使用的調製技術,它們被分類如下。
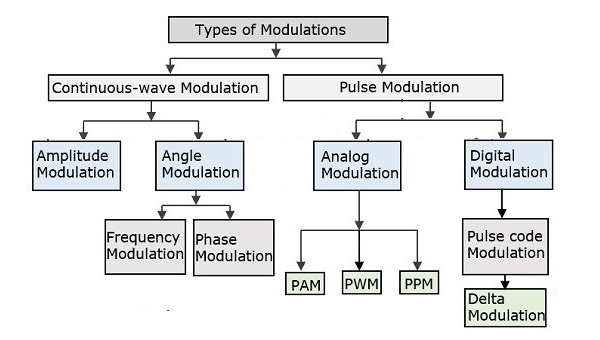
調製型別主要分為連續波調製和脈衝調製。
連續波調製
在連續波調製中,高頻正弦波用作載波。這進一步分為幅度調製和角調製。
如果高頻載波的幅度根據調製訊號的瞬時幅度變化,則這種技術稱為幅度調製。
如果載波的角度根據調製訊號的瞬時值變化,則這種技術稱為角調製。角調製進一步分為頻率調製和相位調製。
如果載波的頻率根據調製訊號的瞬時值變化,則這種技術稱為頻率調製。
如果高頻載波的相位根據調製訊號的瞬時值變化,則這種技術稱為相位調製。
脈衝調製
在脈衝調製中,週期性的矩形脈衝序列用作載波。這進一步分為模擬調製和數字調製。
在模擬調製技術中,如果脈衝的幅度或持續時間或位置根據基帶調製訊號的瞬時值變化,則這種技術稱為脈衝幅度調製 (PAM) 或脈衝持續時間/寬度調製 (PDM/PWM) 或脈衝位置調製 (PPM)。
在數字調製中,使用的調製技術是脈衝編碼調製 (PCM),其中模擬訊號轉換為 1 和 0 的數字形式。由於結果是編碼脈衝序列,因此稱為 PCM。這進一步發展為增量調製 (DM)。這些數字調製技術將在我們的數字通訊教程中討論。
幅度調製
連續波持續不斷,沒有任何間隔,它是包含資訊的基帶訊息訊號。此波必須進行調製。
根據標準定義,“載波訊號的幅度根據調製訊號的瞬時幅度變化。”這意味著不包含資訊的載波訊號的幅度在每個時刻都根據包含資訊的訊號的幅度變化。這可以透過下圖很好地解釋。



第一個圖顯示調製波,也就是訊息訊號。下一個是載波,它是一個高頻訊號,不包含任何資訊。而最後一個是產生的調製波。
可以觀察到,載波的正負峰值用一條虛線連線起來。這條線有助於重現調製訊號的精確形狀。載波上的這條虛線稱為**包絡線**。它與訊息訊號的包絡線相同。
數學表示式
以下是這些波形的數學表示式。
波形的時間域表示
設調製訊號為:
$$m\left ( t \right )=A_m\cos\left ( 2\pi f_mt \right )$$
載波訊號為:
$$c\left ( t \right )=A_c\cos\left ( 2\pi f_ct \right )$$
其中:
$A_m$ 和 $A_c$ 分別是調製訊號和載波訊號的幅度。
$f_m$ 和 $f_c$ 分別是調製訊號和載波訊號的頻率。
那麼,幅度調製波的方程將是
$s(t)= \left [ A_c+A_m\cos\left ( 2\pi f_mt \right ) \right ]\cos \left ( 2\pi f_ct \right )$ (公式1)
調製指數
載波經過調製後,如果計算調製電平,則這種嘗試稱為**調製指數**或**調製深度**。它表示載波所經歷的調製程度。
將公式1重新排列如下:
$s(t)=A_c\left [ 1+\left ( \frac{A_m}{A_c} \right )\cos \left ( 2\pi f_mt \right ) \right ]\cos \left ( 2\pi f_ct \right )$
$\Rightarrow s\left ( t \right ) = A_c\left [ 1 + \mu \cos \left ( 2 \pi f_m t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$ (公式2)
其中,$\mu$ 是調製指數,等於 $A_m$ 和 $A_c$ 的比值。數學上,我們可以寫成
$\mu = \frac{A_m}{A_c}$ (公式3)
因此,當已知訊息訊號和載波訊號的幅度時,我們可以使用上述公式計算調製指數的值。
現在,讓我們透過考慮公式1推匯出另一個調製指數公式。當已知調製波的最大和最小幅度時,我們可以使用此公式計算調製指數值。
設 $A_\max$ 和 $A_\min$ 為調製波的最大和最小幅度。
當 $\cos \left ( 2\pi f_mt \right )$ 為 1 時,我們將得到調製波的最大幅度。
$\Rightarrow A_\max = A_c + A_m$ (公式4)
當 $\cos \left ( 2\pi f_mt \right )$ 為 -1 時,我們將得到調製波的最小幅度。
$\Rightarrow A_\min = A_c - A_m$ (公式5)
將公式4和公式5相加。
$$A_\max + A_\min = A_c+A_m+A_c-A_m = 2A_c$$
$\Rightarrow A_c = \frac{A_\max + A_\min}{2}$ (公式6)
從公式4中減去公式5。
$$A_\max - A_\min = A_c + A_m - \left (A_c -A_m \right )=2A_m$$
$\Rightarrow A_m = \frac{A_\max - A_\min}{2}$ (公式7)
公式7和公式6的比值如下。
$$\frac{A_m}{A_c} = \frac{\left ( A_{max} - A_{min}\right )/2}{\left ( A_{max} + A_{min}\right )/2}$$
$\Rightarrow \mu = \frac{A_\max - A_\min}{A_\max + A_\min}$ (公式8)
因此,公式3和公式8是調製指數的兩個公式。調製指數或調製深度通常以百分比表示,稱為調製百分比。我們只需將調製指數值乘以100即可得到**調製百分比**。
對於完美的調製,調製指數的值應為1,這意味著調製百分比應為100%。
例如,如果此值小於1,即調製指數為0.5,則調製輸出將類似於下圖。這稱為**欠調製**。這種波稱為**欠調波**。

如果調製指數的值大於1,例如1.5左右,則該波將是**過調波**。它將類似於下圖。

隨著調製指數值的增加,載波會經歷180o的相位反轉,這會導致額外的邊帶,從而使波形失真。這種過調波會導致干擾,無法消除。
AM波的頻寬
**頻寬**(BW)是訊號最高頻率和最低頻率之間的差值。數學上,我們可以寫成
$$BW = f_{max} - f_{min}$$
考慮以下幅度調製波的方程。
$$s\left ( t \right ) = A_c\left [ 1 + \mu \cos \left ( 2 \pi f_m t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
$$\Rightarrow s\left ( t \right ) = A_c\cos \left ( 2\pi f_ct \right )+ A_c\mu \cos(2\pi f_ct)\cos \left ( 2\pi f_mt \right )$$
$\Rightarrow s\left ( t \right )= A_c\cos \left ( 2\pi f_ct \right )+\frac{A_c\mu }{2}\cos \left [ 2\pi \left ( f_c+f_m \right ) t\right ]+\frac{A_c\mu }{2}\cos \left [ 2\pi \left ( f_c-f_m \right ) t\right ]$
因此,幅度調製波具有三個頻率。它們是載波頻率 $f_c$、上邊帶頻率 $f_c + f_m$ 和下邊帶頻率 $f_c-f_m$
這裡:
$f_{max}=f_c+f_m$ 和 $f_{min}=f_c-f_m$
將 $f_{max}$ 和 $f_{min}$ 的值代入頻寬公式。
$$BW=f_c+f_m-\left ( f_c-f_m \right )$$
$$\Rightarrow BW=2f_m$$
因此,可以說幅度調製波所需的頻寬是調製訊號頻率的兩倍。
AM波的功率計算
考慮以下幅度調製波的方程。
$\ s\left ( t \right )= A_c\cos \left ( 2\pi f_ct \right )+\frac{A_c\mu }{2}\cos \left [ 2\pi \left ( f_c+f_m \right ) t\right ]+\frac{A_c\mu }{2}\cos \left [ 2\pi \left ( f_c-f_m \right ) t\right ]$
AM波的功率等於載波、上邊帶和下邊帶頻率分量的功率之和。
$$P_t=P_c+P_{USB}+P_{LSB}$$
我們知道餘弦訊號功率的標準公式是
$$P=\frac{{v_{rms}}^{2}}{R}=\frac{\left ( v_m/ \sqrt{2}\right )^2}{2}$$
其中:
$v_{rms}$ 是餘弦訊號的有效值。
$v_m$ 是餘弦訊號的峰值。
首先,讓我們依次找到載波、上邊帶和下邊帶的功率。
載波功率
$$P_c=\frac{\left ( A_c/\sqrt{2} \right )^2}{R}=\frac{{A_{c}}^{2}}{2R}$$
上邊帶功率
$$P_{USB}=\frac{\left ( A_c\mu /2\sqrt{2} \right )^2}{R}=\frac{{A_{c}}^{2}{_{\mu }}^{2}}{8R}$$
類似地,我們將得到下邊帶功率與上邊帶功率相同。
$$P_{LSB}=\frac{{A_{c}}^{2}{_{\mu }}^{2}}{8R}$$
現在,讓我們將這三個功率相加以獲得AM波的功率。
$$P_t=\frac{{A_{c}}^{2}}{2R}+\frac{{A_{c}}^{2}{_{\mu }}^{2}}{8R}+\frac{{A_{c}}^{2}{_{\mu }}^{2}}{8R}$$
$$\Rightarrow P_t=\left ( \frac{{A_{c}}^{2}}{2R} \right )\left ( 1+\frac{\mu ^2}{4}+\frac{\mu ^2}{4} \right )$$
$$\Rightarrow P_t=P_c\left ( 1+\frac{\mu ^2}{2} \right )$$
當已知載波功率和調製指數時,我們可以使用上述公式計算AM波的功率。
如果調製指數 $\mu=1$,則AM波的功率等於載波功率的1.5倍。因此,對於完美的調製,傳輸AM波所需的功率是載波功率的1.5倍。
數值問題1
在上一章中,我們討論了幅度調製中使用的引數。每個引數都有自己的公式。透過使用這些公式,我們可以找到相應的引數值。在本章中,讓我們解決一些基於幅度調製概念的問題。
問題1
調製訊號 $m\left ( t \right )=10 \cos \left ( 2\pi \times 10^3 t\right )$ 用載波訊號 $c\left ( t \right )=50 \cos \left ( 2\pi \times 10^5 t\right )$ 進行幅度調製。求調製指數、載波功率和傳輸AM波所需的功率。
解答
已知調製訊號的方程為
$$m\left ( t \right )=10\cos \left ( 2\pi \times 10^3 t\right )$$
我們知道調製訊號的標準方程為
$$m\left ( t \right )=A_m\cos\left ( 2\pi f_mt \right )$$
透過比較以上兩個方程,我們將得到
調製訊號的幅度為 $A_m=10$ 伏
調製訊號的頻率為 $$f_m=10^3 Hz=1 KHz$$
已知載波訊號的方程為
$$c\left ( t \right )=50\cos \left ( 2\pi \times 10^5t \right )$$
載波訊號的標準方程為
$$c\left ( t \right )=A_c\cos\left ( 2\pi f_ct \right )$$
透過比較這兩個方程,我們將得到
載波訊號的幅度為 $A_c=50$ 伏
載波訊號的頻率為 $f_c=10^5 Hz=100 KHz$
我們知道調製指數的公式為
$$\mu =\frac{A_m}{A_c}$$
將 $A_m$ 和 $A_c$ 的值代入上述公式。
$$\mu=\frac{10}{50}=0.2$$
因此,**調製指數的值為0.2**,調製百分比為20%。
載波功率 $P_c$ 的公式為
$$P_c=\frac{{A_{c}}^{2}}{2R}$$
假設 $R=1\Omega$ 並將 $A_c$ 的值代入上述公式。
$$P_c=\frac{\left ( 50 \right )^2}{2\left ( 1 \right )}=1250W$$
因此,**載波功率** $P_c$ 為**1250瓦**。
我們知道**傳輸AM波所需的功率**的公式為
$$\Rightarrow P_t=P_c\left ( 1+\frac{\mu ^2}{2} \right )$$
將 $P_c$ 和 $\mu$ 的值代入上述公式。
$$P_t=1250\left ( 1+\frac{\left ( 0.2 \right )^2}{2} \right )=1275W$$
因此,**傳輸AM波所需的功率**為**1275瓦**。
問題2
幅度波的方程由 $s\left ( t \right ) = 20\left [ 1 + 0.8 \cos \left ( 2\pi \times 10^3t \right ) \right ]\cos \left ( 4\pi \times 10^5t \right )$ 給出。求載波功率、總邊帶功率和AM波的頻寬。
解答
已知幅度調製波的方程為
$$s\left ( t \right )=20\left [ 1+0.8 \cos\left ( 2\pi \times 10^3t \right ) \right ]\cos \left ( 4\pi \times 10^5t \right )$$
將上述方程改寫為
$$s\left ( t \right )=20\left [ 1+0.8 \cos\left ( 2\pi \times 10^3t \right ) \right ]\cos \left ( 2\pi \times 2 \times 10^5t \right )$$
我們知道幅度調製波的方程為
$$s\left ( t \right )=A_c\left [ 1+\mu \cos\left ( 2\pi f_mt \right ) \right ]\cos\left ( 2 \pi f_ct \right )$$
透過比較以上兩個方程,我們將得到
載波訊號的幅度為 $A_c=20$ 伏
調製指數為 $\mu=0.8$
調製訊號的頻率為 $f_m=10^3Hz=1 KHz$
載波訊號的頻率為 $f_c=2\times 10^5Hz=200KHz$
載波功率 $P_c$ 的公式為
$$P_c=\frac{{A_{e}}^{2}}{2R}$$
假設 $R=1\Omega$ 並將 $A_c$ 的值代入上述公式。
$$P_c=\frac{\left ( 20 \right )^2}{2\left ( 1 \right )}=200W$$
因此,**載波功率** $P_c$ 為**200瓦**。
我們知道總邊帶功率的公式為
$$P_{SB}=\frac{P_c\mu^2}{2}$$
將 $P_c$ 和 $\mu$ 的值代入上述公式。
$$P_{SB}=\frac{200\times \left ( 0.8 \right )^2}{2}=64W$$
因此,**總邊帶功率**為**64瓦**。
我們知道AM波頻寬的公式為
$$BW=2f_m$$
將 $f_m$ 的值代入上述公式。
$$BW=2\left ( 1K \right )=2 KHz$$
因此,AM波的**頻寬**為**2 KHz**。
模擬通訊 - AM調製器
在本章中,我們將討論生成幅度調製波的調製器。以下兩個調製器生成AM波。
- 平方律調製器
- 開關調製器
平方律調製器
以下是平方律調製器的框圖
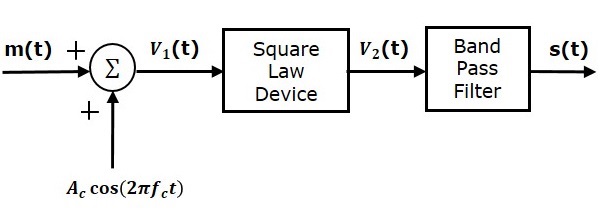
設調製訊號和載波訊號分別表示為 $m\left ( t \right )$ 和 $A\cos\left ( 2\pi f_ct\right )$。這兩個訊號作為輸入應用於加法器模組。此加法器模組產生一個輸出,它是調製訊號和載波訊號的加法。數學上,我們可以寫成
$$V_1t=m\left ( t \right )+A_c\cos\left ( 2 \pi f_ct \right )$$
該訊號 $V_1t$ 被用作二極體等非線性器件的輸入。二極體的特性與平方律密切相關。
$V_2t=k_1V_1\left ( t \right )+k_2V_1^2\left ( t \right )$(公式 1)
其中,$k_1$ 和 $k_2$ 是常數。
將 $V_1\left (t \right )$ 代入公式 1
$$V_2\left (t\right ) = k_1\left [ m\left ( t \right ) + A_c \cos \left ( 2 \pi f_ct \right ) \right ] + k_2\left [ m\left ( t \right ) + A_c \cos\left ( 2 \pi f_ct \right ) \right ]^2$$
$\Rightarrow V_2\left (t\right ) = k_1 m\left ( t \right ) +k_1 A_c \cos \left ( 2 \pi f_ct \right ) +k_2 m^2\left ( t \right ) +$
$ k_2A_c^2 \cos^2\left ( 2 \pi f_ct \right )+2k_2m\left ( t \right )A_c \cos\left ( 2 \pi f_ct \right )$
$\Rightarrow V_2\left (t\right ) = k_1 m\left ( t \right ) +k_2 m^2\left ( t \right ) +k_2 A^2_c \cos^2 \left ( 2 \pi f_ct \right ) +$
$k_1A_c\left [ 1+\left ( \frac{2k_2}{k_1} \right )m\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$
上述公式的最後一項表示所需的調幅波,而前三項是不需要的。因此,藉助帶通濾波器,我們可以只通過調幅波並消除前三項。
因此,平方律調製器的輸出為
$$s\left ( t \right )=k_1A_c\left [1+\left ( \frac{2k_2}{k_1} \right ) m\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
調幅波的標準方程為
$$s\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos \left (2 \pi f_ct \right )$$
其中,$K_a$ 是幅度靈敏度
透過將平方律調製器的輸出與調幅波的標準方程進行比較,我們將得到比例因子為 $k_1$,幅度靈敏度 $k_a$ 為 $\frac{2k_2}{k1}$。
開關調製器
以下是開關調製器的框圖。
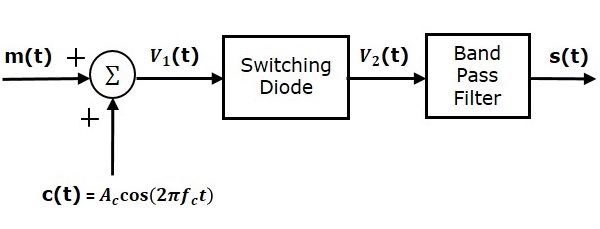
開關調製器類似於平方律調製器。唯一的區別在於,在平方律調製器中,二極體工作在非線性模式,而在開關調製器中,二極體必須作為理想開關工作。
設調製訊號和載波訊號分別表示為 $m\left ( t \right )$ 和 $c\left ( t \right )= A_c \cos\left ( 2\pi f_ct \right )$。這兩個訊號被用作加法器塊的輸入。加法器塊產生一個輸出,該輸出是調製訊號和載波訊號的加和。在數學上,我們可以將其寫成
$$V_1\left ( t \right )=m\left ( t \right )+c\left ( t \right )= m\left ( t \right )+A_c \cos\left ( 2 \pi f_ct \right )$$
該訊號 $V_1\left ( t \right )$ 被用作二極體的輸入。假設,與載波訊號 $A_c$ 的幅度相比,調製訊號的幅度非常小。因此,二極體的通斷動作由載波訊號 $c\left ( t \right )$ 控制。這意味著,當 $c\left ( t \right )> 0$ 時,二極體將正向偏置,當 $c\left ( t \right )< 0$ 時,二極體將反向偏置。
因此,二極體的輸出為
$$V_2 \left ( t \right )=\left\{\begin{matrix} V_1\left ( t \right )& if &c\left ( t \right )>0 \\ 0& if & c\left ( t \right )<0 \end{matrix}\right.$$
我們可以將其近似為
$V_2\left ( t \right ) = V_1\left ( t \right )x\left ( t \right )$(公式 2)
其中,$x\left ( t \right )$ 是週期脈衝序列,週期為 $T=\frac{1}{f_c}$

該週期脈衝序列的傅立葉級數表示為
$$x\left ( t \right )=\frac{1}{2}+\frac{2}{\pi }\sum_{n=1}^{\infty}\frac{\left ( -1 \right )^n-1}{2n-1} \cos\left (2 \pi \left ( 2n-1 \right ) f_ct \right )$$
$$\Rightarrow x\left ( t \right )=\frac{1}{2}+\frac{2}{\pi} \cos\left ( 2 \pi f_ct \right )-\frac{2}{3\pi } \cos\left ( 6 \pi f_ct \right ) +....$$
將 $V_1\left ( t \right )$ 和 $x\left ( t \right )$ 的值代入公式 2。
$V_2\left ( t \right )=\left [ m\left ( t \right )+A_c \cos\left ( 2 \pi f_ct \right ) \right ] \left [ \frac{1}{2} + \frac{2}{\pi} \cos \left ( 2 \pi f_ct \right )-\frac{2}{3\pi} \cos\left ( 6 \pi f_ct \right )+.....\right ]$
$V_2\left ( t \right )=\frac{m\left ( t \right )}{2}+\frac{A_c}{2} \cos\left ( 2 \pi f_ct \right )+\frac{2m\left ( t \right )}{\pi} \cos\left ( 2 \pi f_ct \right ) +\frac{2A_c}{\pi} \cos^2\left ( 2 \pi f_ct \right )-$
$\frac{2m\left ( t \right )}{3\pi} \cos\left ( 6 \pi f_ct \right )-\frac{2A_c}{3\pi}\cos \left ( 2 \pi f_ct \right ) \cos\left ( 6 \pi f_ct \right )+..... $
$V_2\left ( t \right )=\frac{A_c}{2}\left ( 1+\left ( \frac{4}{\pi A_c} \right )m\left ( t \right ) \right ) \cos\left ( 2 \pi f_ct \right ) + \frac{m\left ( t \right )}{2}+\frac{2A_c}{\pi} \cos^2\left ( 2 \pi f_ct \right )-$
$\frac{2m\left ( t \right )}{3 \pi} \cos\left ( 6 \pi f_ct \right )-\frac{2A_c}{3\pi} \cos\left ( 2 \pi f_ct \right ) \cos\left ( 6 \pi f_ct \right )+.....$
上述方程的第 1 項表示所需的調幅波,其餘項是不需要的項。因此,藉助帶通濾波器,我們可以只通過調幅波並消除其餘項。
因此,開關調製器的輸出為
$$s\left ( t \right )=\frac{A_c}{2}\left ( 1+\left ( \frac{4}{\pi A_c} \right ) m\left ( t \right )\right ) \cos\left ( 2 \pi f_ct \right )$$
我們知道調幅波的標準方程為
$$s\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
其中,$k_a$ 是幅度靈敏度。
透過將開關調製器的輸出與調幅波的標準方程進行比較,我們將得到比例因子為 0.5,幅度靈敏度 $k_a$ 為 $\frac{4}{\pi A_c}$ 。
模擬通訊 - 調幅解調器
從調製波中提取原始訊息訊號的過程稱為檢波或解調。用於解調調製波的電路稱為解調器。以下解調器(檢波器)用於解調調幅波。
- 平方律解調器
- 包絡檢波器
平方律解調器
平方律解調器用於解調低電平調幅波。以下是平方律解調器的框圖。

該解調器包含一個平方律器件和一個低通濾波器。調幅波 $V_1\left ( t \right )$ 被用作該解調器的輸入。
調幅波的標準形式為
$$V_1\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
我們知道,平方律器件的輸入和輸出之間的數學關係為
$V_2\left ( t \right )=k_1V_1\left ( t \right )+k_2V_1^2\left ( t \right )$(公式 1)
其中:
$V_1\left ( t \right )$ 是平方律器件的輸入,它就是調幅波
$V_2\left ( t \right )$ 是平方律器件的輸出
$k_1$ 和 $k_2$ 是常數
將 $V_1\left ( t \right )$ 代入公式 1
$$V_2\left ( t \right )=k_1\left ( A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )\right )+k_2\left ( A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )\right )^2$$
$\Rightarrow V_2\left ( t \right )=k_1A_c \cos \left ( 2 \pi f_ct \right )+k_1A_ck_am\left ( t \right ) \cos \left ( 2 \pi f_ct \right )+$
$k_2{A_{c}}^{2}\left [ 1+{K_{a}}^{2}m^2\left ( t \right )+2k_am\left ( t \right ) \right ]\left ( \frac{1+ \cos\left ( 4 \pi f_ct \right )}{2} \right )$
$\Rightarrow V_2\left ( t \right )=k_1A_c \cos \left ( 2 \pi f_ct \right )+k_1A_ck_am\left ( t \right ) \cos \left ( 2 \pi f_ct \right)+\frac{K_2{A_{c}}^{2}}{2}+$
$\frac{K_2{A_{c}}^{2}}{2} \cos \left ( 4 \pi f_ct \right )+\frac{k_2 {A_{c}}^{2}{k_{a}}^{2}m^2\left ( t \right )}{2}+\frac{k_2 {A_{c}}^{2}{k_{a}}^{2}m^2\left ( t \right )}{2} \cos\left ( 4 \pi f_ct \right )+$
$k_2{A_{c}}^{2}k_am\left ( t \right )+k_2{A_{c}}^{2}k_am\left ( t \right )\cos \left ( 4 \pi f_ct \right )$
在上述公式中,項 $k_2{A_{c}}^{2}k_am\left ( t \right )$ 是訊息訊號的縮放版本。可以透過使上述訊號透過低通濾波器來提取它,並且直流分量 $\frac{k_2{A_{c}}^{2}}{2}$ 可以藉助耦合電容器消除。
包絡檢波器
包絡檢波器用於檢測(解調)高電平調幅波。以下是包絡檢波器的框圖。
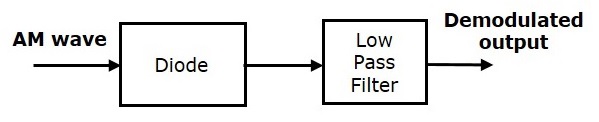
該包絡檢波器由一個二極體和一個低通濾波器組成。這裡,二極體是主要的檢測元件。因此,包絡檢波器也稱為二極體檢波器。低通濾波器包含電阻和電容器的並聯組合。
調幅波 $s\left ( t \right )$ 被用作該檢波器的輸入。
我們知道調幅波的標準形式為
$$s\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
在調幅波的正半週期,二極體導通,電容器充電到調幅波的峰值。當調幅波的值小於該值時,二極體將反向偏置。因此,電容器將透過電阻R放電,直到調幅波的下一個正半週期。當調幅波的值大於電容器電壓時,二極體導通,該過程將重複。
我們應該選擇元件值,以便電容器快速充電並緩慢放電。結果,我們將獲得與調幅波包絡相同的電容器電壓波形,該波形幾乎類似於調製訊號。
模擬通訊 - 雙邊帶抑制載波調製
在幅度調製過程中,調製波由載波和兩個邊帶組成。調製波的資訊僅包含在邊帶中。邊帶只不過是一段包含功率的頻率帶,它是載波頻率的較低和較高頻率。
傳輸包含載波和兩個邊帶的訊號可以稱為雙邊帶全載波系統,或簡稱為DSBFC。其波形圖如下所示。

然而,這種傳輸效率低下。因為,載波中浪費了三分之二的功率,而載波不攜帶任何資訊。
如果抑制此載波並將節省的功率分配到兩個邊帶,則此過程稱為雙邊帶抑制載波系統,或簡稱為DSBSC。其波形圖如下所示。

數學表示式
讓我們考慮與前面章節中相同的調製和載波訊號的數學表示式。
即,調製訊號
$$m\left ( t \right )=A_m \cos \left ( 2 \pi f_mt\right )$$
載波訊號
$$c\left ( t \right )=A_c \cos \left ( 2 \pi f_ct\right )$$
在數學上,我們可以將DSBSC波的方程表示為調製和載波訊號的乘積。
$$s\left ( t \right )=m\left ( t \right )c\left ( t \right )$$
$$\Rightarrow s\left ( t \right )=A_mA_c \cos \left ( 2 \pi f_mt \right )\cos \left ( 2 \pi f_ct \right )$$
DSBSC波的頻寬
我們知道頻寬(BW)的公式是
$$BW=f_{max}-f_{min}$$
考慮DSBSC調製波的方程。
$$s\left ( t \right )=A_mA_c \cos\left ( 2 \pi f_mt \right ) \cos(2 \pi f_ct)$$
$$\Rightarrow s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right ) t\right ]+\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c-f_m \right ) t\right ]$$
DSBSC調製波只有兩個頻率。因此,最大頻率和最小頻率分別為$f_c+f_m$和$f_c-f_m$。
即,
$f_{max}=f_c+f_m$ 和 $f_{min}=f_c-f_m$
將$f_{max}$和$f_{min}$的值代入頻寬公式。
$$BW=f_c+f_m-\left ( f_c-f_m \right )$$
$$\Rightarrow BW=2f_m$$
因此,DSBSC波的頻寬與AM波相同,等於調製訊號頻率的兩倍。
DSBSC波的功率計算
考慮以下DSBSC調製波的方程。
$$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c+f_m \right ) t\right ]+\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c-f_m \right ) t\right ]$$
DSBSC波的功率等於上邊帶和下邊帶頻率分量的功率之和。
$$P_t=P_{USB}+P_{LSB}$$
我們知道餘弦訊號功率的標準公式是
$$P=\frac{{v_{rms}}^{2}}{R}=\frac{\left ( v_m\sqrt{2}\right )^2}{R}$$
首先,讓我們分別求出上邊帶和下邊帶的功率。
上邊帶功率
$$P_{USB}=\frac{\left ( A_mA_c / 2\sqrt{2}\right )^2}{R}=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$
類似地,我們將得到下邊帶功率與上邊帶功率相同。
$$P_{USB}=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$
現在,讓我們將這兩個邊帶功率相加,以得到DSBSC波的功率。
$$P_t=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}+\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$
$$\Rightarrow P_t=\frac{{A_{m}}^{2}{A_{c}}^{2}}{4R}$$
因此,傳輸DSBSC波所需的功率等於兩個邊帶的功率之和。
模擬通訊 - DSBSC調製器
在本章中,讓我們討論生成DSBSC波的調製器。以下兩個調製器生成DSBSC波。
- 平衡調製器
- 環形調製器
平衡調製器
以下是平衡調製器的框圖。

平衡調製器由兩個相同的AM調製器組成。這兩個調製器以平衡配置佈置,以抑制載波訊號。因此,它被稱為平衡調製器。
相同的載波訊號$c\left ( t \right )= A_c \cos \left ( 2 \pi f_ct \right )$作為這兩個AM調製器輸入之一。調製訊號$m\left ( t \right )$作為另一個輸入應用於上AM調製器。而極性相反的調製訊號$m\left ( t \right )$,即$-m\left ( t \right )$,作為另一個輸入應用於下AM調製器。
上AM調製器的輸出為
$$s_1\left ( t \right )=A_c\left [1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
下AM調製器的輸出為
$$s_2\left ( t \right )=A_c\left [1-k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
我們透過從$s_1\left ( t \right )$中減去$s_2\left ( t \right )$來獲得DSBSC波$s\left ( t \right )$。加法器模組用於執行此操作。帶有正號的$s_1\left ( t \right )$和帶有負號的$s_2\left ( t \right )$作為輸入應用於加法器模組。因此,加法器模組產生輸出$s\left ( t \right )$,它是$s_1\left ( t \right )$和$s_2\left ( t \right )$的差。
$$\Rightarrow s\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )-A_c\left [ 1-k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
$$\Rightarrow s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )+A_ck_am\left ( t \right ) \cos\left ( 2 \pi f_ct \right )- A_c \cos\left ( 2 \pi f_ct \right )+$$
$A_ck_am\left ( t \right ) \cos\left ( 2 \pi f_ct \right )$
$\Rightarrow s\left ( t \right )=2A_ck_am\left ( t \right ) \cos\left ( 2 \pi f_ct \right )$
我們知道DSBSC波的標準方程是
$$s\left ( t \right )=A_cm \left ( t \right ) \cos\left ( 2 \pi f_ct \right )$$
透過將加法器模組的輸出與DSBSC波的標準方程進行比較,我們將得到比例因子為$2k_a$。
環形調製器
以下是環形調製器的框圖。
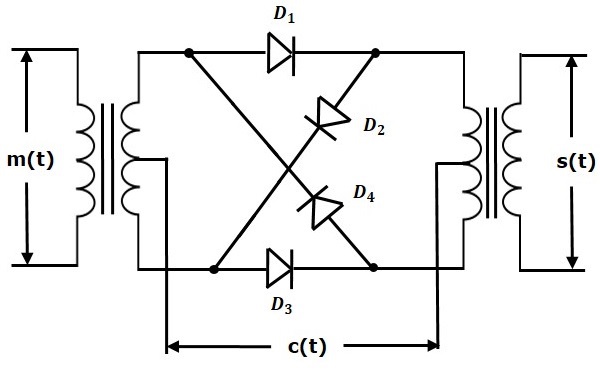
在此圖中,四個二極體$D_1$、$D_2$、$D_3$和$D_4$以環形結構連線。因此,此調製器稱為環形調製器。在此圖中使用了兩個中心抽頭的變壓器。訊息訊號$m\left ( t \right )$應用於輸入變壓器。而載波訊號$c\left ( t \right )$應用於兩個中心抽頭的變壓器之間。
對於載波訊號的正半週期,二極體$D_1$和$D_3$導通,其他兩個二極體$D_2$和$D_4$關閉。在這種情況下,訊息訊號乘以+1。
對於載波訊號的負半週期,二極體$D_2$和$D_4$導通,其他兩個二極體$D_1$和$D_3$關閉。在這種情況下,訊息訊號乘以-1。這導致所得DSBSC波發生$180^0$相移。
從以上分析可以看出,四個二極體$D_1$、$D_2$、$D_3$和$D_4$受載波訊號控制。如果載波是方波,則$c\left ( t \right )$的傅立葉級數表示為
$$c\left ( t \right )=\frac{4}{\pi}\sum_{n=1}^{\infty }\frac{\left ( -1 \right )^{n-1}}{2n-1} \cos\left [2 \pi f_ct\left ( 2n-1 \right ) \right ]$$
我們將得到DSBSC波$s\left ( t \right )$,它只是載波訊號$c\left ( t \right )$和訊息訊號$m\left ( t \right )$的乘積,即
$$s\left ( t \right )=\frac{4}{\pi}\sum_{n=1}^{\infty }\frac{\left ( -1 \right )^{n-1}}{2n-1} \cos\left [2 \pi f_ct\left ( 2n-1 \right ) \right ]m\left ( t \right )$$
上述方程表示在環形調製器的輸出變壓器處獲得的DSBSC波。
DSBSC調製器也稱為乘積調製器,因為它們產生的輸出是兩個輸入訊號的乘積。
雙邊帶抑制載波解調器
從DSBSC波中提取原始訊息訊號的過程稱為DSBSC的檢測或解調。以下解調器(檢測器)用於解調DSBSC波。
- 相干檢測器
- 科斯塔斯環路
相干檢測器
這裡,使用相同的載波訊號(用於生成DSBSC訊號)來檢測訊息訊號。因此,這種檢測過程稱為相干或同步檢測。以下是相干檢測器的框圖。
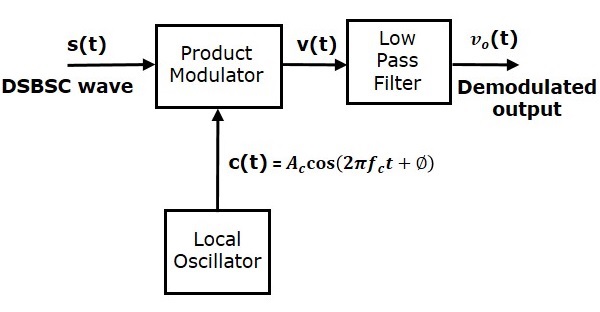
在此過程中,可以透過將DSBSC波與具有與DSBSC調製中使用的載波相同頻率和相位的載波相乘來從DSBSC波中提取訊息訊號。然後將所得訊號透過低通濾波器。此濾波器的輸出是所需的訊息訊號。
令DSBSC波為
$$s\left ( t \right )= A_c \cos\left ( 2 \pi f_ct \right )m \left ( t \right )$$
本地振盪器的輸出為
$$c\left ( t \right )= A_c \cos\left ( 2 \pi f_ct+ \phi \right )$$
其中,$\phi$是本地振盪器訊號與用於DSBSC調製的載波訊號之間的相位差。
從圖中,我們可以將乘積調製器的輸出寫為
$$v\left ( t \right )=s\left ( t \right )c\left ( t \right )$$
將$s\left ( t \right )$和$c\left ( t \right )$的值代入上述方程。
$$\Rightarrow v\left ( t \right )=A_c \cos \left ( 2 \pi f_ct \right )m\left ( t \right )A_c \cos \left ( 2 \pi f_ct + \phi \right )$$
$={A_{c}}^{2} \cos \left ( 2 \pi f_ct \right ) \cos \left ( 2 \pi f_ct + \phi \right )m\left ( t \right )$
$=\frac{{A_{c}}^{2}}{2}\left [ \cos\left ( 4 \pi f_ct+ \phi \right )+ \cos \phi \right ]m\left ( t \right )$
$$v\left ( t \right )=\frac{{A_{c}}^{2}}{2} \cos\phi m\left ( t \right )+\frac{{A_{c}}^{2}}{2} \cos \left ( 4 \pi f_ct+ \phi \right )m\left ( t \right )$$
在上式中,第一項是訊息訊號的縮放版本。可以透過將上述訊號透過低通濾波器來提取它。
因此,低通濾波器的輸出為
$$v_0t=\frac{{A_{c}}^{2}}{2} \cos \phi m \left ( t \right )$$
當$\phi=0^0$時,解調訊號幅度最大。這就是為什麼本地振盪器訊號和載波訊號應該同相,即這兩個訊號之間不應該有任何相位差。
當$\phi=\pm 90^0$時,解調訊號幅度將為零。這種效應稱為正交零效應。
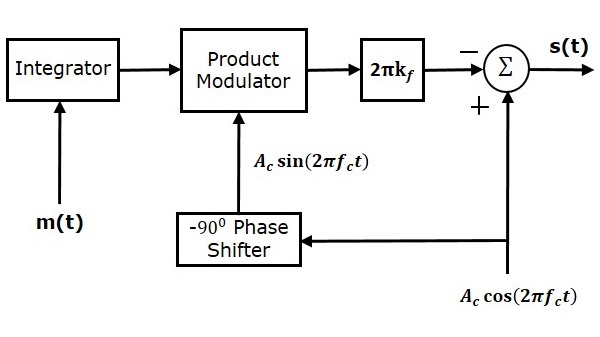
科斯塔斯環路
科斯塔斯環路用於使載波訊號(用於DSBSC調製)和本地生成的訊號同相。以下是科斯塔斯環路的框圖。
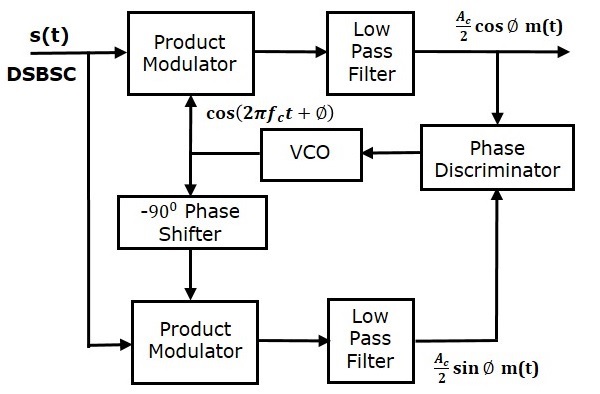
科斯塔斯環路由兩個乘積調製器組成,它們具有共同的輸入$s\left ( t \right )$,它是DSBSC波。兩個乘積調製器的另一個輸入來自壓控振盪器(VCO),其中一個乘積調製器具有$-90^0$相移,如圖所示。
我們知道DSBSC波的方程是
$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )m\left ( t \right )$$
令VCO的輸出為
$$c_1\left ( t \right )=\cos\left ( 2 \pi f_ct + \phi\right )$$
此VCO輸出作為上乘積調製器的載波輸入。
因此,上路乘積調製器的輸出為
$$v_1\left ( t \right )=s\left ( t \right )c_1\left ( t \right )$$
將 $s\left ( t \right )$ 和 $c_1\left ( t \right )$ 的值代入上式。
$$\Rightarrow v_1\left ( t \right )=A_c \cos \left ( 2 \pi f_ct \right )m\left ( t \right ) \cos\left ( 2 \pi f_ct + \phi \right )$$
簡化後,得到 $v_1\left ( t \right )$ 為
$$v_1\left ( t \right )=\frac{A_c}{2} \cos \phi m\left ( t \right )+\frac{A_c}{2} \cos\left ( 4 \pi f_ct + \phi \right )m\left ( t \right )$$
該訊號作為上路低通濾波器的輸入。該低通濾波器的輸出為
$$v_{01}\left ( t \right )=\frac{A_c}{2} \cos \phi m\left ( t \right )$$
因此,該低通濾波器的輸出是調製訊號的縮放版本。
-90° 移相器的輸出為
$$c_2\left ( t \right )=cos\left ( 2 \pi f_ct + \phi-90^0 \right )= \sin\left ( 2 \pi f_ct + \phi \right )$$
該訊號作為下路乘積調製器的載波輸入。
下路乘積調製器的輸出為
$$v_2\left ( t \right )=s\left ( t \right )c_2\left ( t \right )$$
將 $s\left ( t \right )$ 和 $c_2\left ( t \right )$ 的值代入上式。
$$\Rightarrow v_2\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )m\left ( t \right ) \sin \left ( 2 \pi f_ct + \phi \right )$$
簡化後,得到 $v_2\left ( t \right )$ 為
$$v_2\left ( t \right )=\frac{A_c}{2} \sin \phi m\left ( t \right )+\frac{A_c}{2} \sin \left ( 4 \pi f_ct+ \phi \right )m\left ( t \right )$$
該訊號作為下路低通濾波器的輸入。該低通濾波器的輸出為
$$v_{02}\left ( t \right )=\frac{A_c}{2} \sin \phi m\left ( t \right )$$
該低通濾波器的輸出與上路低通濾波器的輸出相差-90°。
這兩個低通濾波器的輸出作為鑑相器的輸入。根據這兩個訊號之間的相位差,鑑相器產生一個直流控制訊號。
該訊號作為壓控振盪器 (VCO) 的輸入,用於校正 VCO 輸出中的相位誤差。因此,載波訊號(用於 DSBSC 調製)和本地生成的訊號(VCO 輸出)同相。
模擬通訊 - 單邊帶抑制載波調製 (SSBSC)
在前面的章節中,我們討論了 DSBSC 調製和解調。DSBSC 調製訊號有兩個邊帶。由於這兩個邊帶攜帶相同的資訊,因此無需傳輸兩個邊帶。我們可以消除一個邊帶。
抑制其中一個邊帶以及載波並傳輸單個邊帶的過程稱為**單邊帶抑制載波**系統,簡稱**SSBSC**。其波形如圖所示。
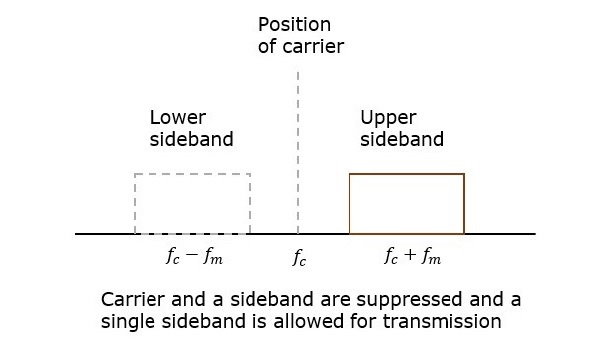
在上圖中,載波和下邊帶被抑制。因此,上邊帶用於傳輸。類似地,我們可以在傳輸下邊帶的同時抑制載波和上邊帶。
這種傳輸單個邊帶的 SSBSC 系統具有高功率,因為分配給載波和另一個邊帶的功率都用於傳輸這個單邊帶。
數學表示式
讓我們考慮與前面章節中相同的調製訊號和載波訊號的數學表示式。
即,調製訊號
$$m\left ( t \right )=A_m \cos\left ( 2 \pi f_mt \right )$$
載波訊號
$$c\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right)$$
在數學上,我們可以將 SSBSC 波的方程表示為
$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right ) t\right ]$對於上邊帶
或者
$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c-f_m \right ) t\right ]$對於下邊帶
SSBSC 波的頻寬
我們知道,DSBSC 調製波包含兩個邊帶,其頻寬為 $2f_m$。由於 SSBSC 調製波只包含一個邊帶,因此其頻寬是 DSBSC 調製波頻寬的一半。
即,SSBSC 調製波的頻寬 =$\frac{2f_m}{2}=f_m$
因此,SSBSC 調製波的頻寬為 $f_m$,等於調製訊號的頻率。
SSBSC 波的功率計算
考慮以下 SSBSC 調製波的方程。
$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right ) t\right ]$對於上邊帶
或者
$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c-f_m \right ) t\right ]$對於下邊帶
SSBSC 波的功率等於任何一個邊帶頻率分量的功率。
$$P_t=P_{USB}=P_{LSB}$$
我們知道餘弦訊號功率的標準公式是
$$P=\frac{{v_{rms}}^{2}}{R}=\frac{\left ( v_m/\sqrt{2} \right )^2}{R}$$
在這種情況下,上邊帶的功率為
$$P_{USB}=\frac{\left ( A_m A_c/2\sqrt{2} \right )^2}{R}=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$
類似地,我們將得到下邊帶功率與上邊帶功率相同。
$$P_{LSB}= \frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$
因此,SSBSC 波的功率為
$$P_t=P_{USB}=P_{LSB}= \frac{{A_{m}}^{2}{A_{c}}^{2}}{8R}$$
優點
頻寬或佔用頻譜空間小於 AM 和 DSBSC 波。
允許傳輸更多數量的訊號。
節省功率。
可以傳輸高功率訊號。
噪聲較少。
訊號衰落不太可能發生。
缺點
SSBSC 波的產生和檢測是一個複雜的過程。
除非 SSB 發射機和接收機具有極佳的頻率穩定性,否則訊號質量會受到影響。
應用
用於節能和低頻寬要求。
在陸地、空中和海上行動通訊中。
在點對點通訊中。
在無線電通訊中。
在電視、遙測和雷達通訊中。
在軍事通訊中,例如業餘無線電等。
模擬通訊 - SSBSC 調製器
在本節中,讓我們討論產生 SSBSC 波的調製器。我們可以使用以下兩種方法生成 SSBSC 波。
- 頻率鑑別法
- 相位鑑別法
頻率鑑別法
下圖顯示了使用頻率鑑別法實現 SSBSC 調製器的框圖。
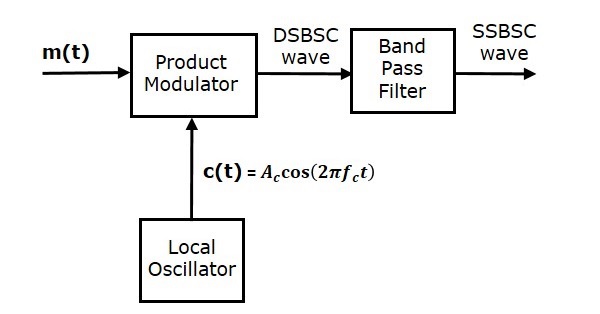
在這種方法中,我們首先使用乘積調製器生成 DSBSC 波。然後,將此 DSBSC 波作為帶通濾波器的輸入。該帶通濾波器產生一個輸出,即 SSBSC 波。
將帶通濾波器的頻率範圍選擇為所需的 SSBSC 波的頻譜。這意味著帶通濾波器可以調諧到上邊帶或下邊帶頻率,以獲得具有上邊帶或下邊帶的相應 SSBSC 波。
相位鑑別法
下圖顯示了使用相位鑑別法實現 SSBSC 調製器的框圖。
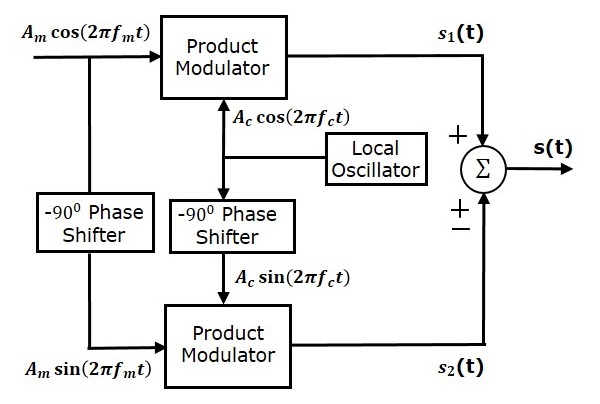
該框圖包括兩個乘積調製器、兩個 -90° 移相器、一個本地振盪器和一個加法器。乘積調製器產生一個輸出,它是兩個輸入的乘積。-90° 移相器產生一個輸出,該輸出相對於輸入延遲 -90°。
本地振盪器用於產生載波訊號。加法器產生一個輸出,該輸出根據輸入的極性,可以是兩個輸入的和或差。
調製訊號 $A_m \cos\left ( 2 \pi f_mt \right )$ 和載波訊號 $A_c \cos\left ( 2 \pi f_ct \right )$ 直接作為上路乘積調製器的輸入。因此,上路乘積調製器產生一個輸出,它是這兩個輸入的乘積。
上路乘積調製器的輸出為
$$s_1\left ( t \right )=A_mA_c \cos \left ( 2 \pi f_mt \right ) \cos\left ( 2 \pi f_ct \right )$$
$$ \Rightarrow s_1\left ( t \right )=\frac{A_mA_c}{2} \left \{ \cos \left [ 2 \pi\left ( f_c+f_m \right )t \right ]+ \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ] \right \}$$
調製訊號 $A_m \cos\left ( 2 \pi f_mt \right )$ 和載波訊號 $A_c \cos\left ( 2 \pi f_ct \right )$ 在作為下路乘積調製器的輸入之前,先進行 -90° 移相。因此,下路乘積調製器產生一個輸出,它是這兩個輸入的乘積。
下路乘積調製器的輸出為
$$s_2\left ( t \right )=A_mA_c \cos\left ( 2 \pi f_mt-90^0 \right ) \cos\left (2 \pi f_ct-90^0 \right )$$
$\Rightarrow s_2\left ( t \right )=A_mA_c \sin \left ( 2 \pi f_mt \right )\sin \left ( 2 \pi f_ct \right )$
$\Rightarrow s_2\left ( t \right )=\frac{A_mA_c}{2} \left \{ \cos \left [ 2 \pi\left ( f_c-f_m \right )t \right ]- \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \right \}$
將 $s_1\left ( t \right )$ 和 $s_2\left ( t \right )$ 相加,以獲得具有下邊帶的 SSBSC 調製波 $s\left ( t \right )$。
$s\left ( t \right )=\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ]+\cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ] \right \}+$
$\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ]-\cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \right \}$
$\Rightarrow s\left ( t \right )=A_mA_c \cos \left [ 2 \pi\left ( f_c-f_m \right )t \right ]$
將 $s_2\left ( t \right )$ 從 $s_1\left ( t \right )$ 中減去,以獲得具有上邊帶的 SSBSC 調製波 $s\left ( t \right )$。
$s\left ( t \right )=\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ]+\cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ] \right \}-$
$\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ]-\cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \right \}$
$\Rightarrow s\left ( t \right )=A_mA_c \cos \left [ 2 \pi\left ( f_c+f_m \right )t \right ]$
因此,透過正確選擇加法器輸入的極性,我們可以得到具有上邊帶或下邊帶的 SSBSC 波。
單邊帶抑制載波解調器
從 SSBSC 波中提取原始訊息訊號的過程稱為 SSBSC 的檢測或解調。相干檢測器用於解調 SSBSC 波。
相干檢測器
這裡,使用相同的載波訊號(用於產生SSB-SC波)來檢測訊息訊號。因此,這種檢測過程稱為**相干**或**同步檢測**。以下是相干檢測器的框圖。

在這個過程中,可以透過將SSB-SC波與具有相同頻率和相位的載波相乘來提取訊息訊號,該載波在SSB-SC調製中使用。然後將得到的訊號透過低通濾波器。該濾波器的輸出是所需的訊息訊號。
考慮以下具有**下邊帶**的**SSB-SC**波。
$$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ]$$
本地振盪器的輸出為
$$c\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )$$
從圖中,我們可以將乘積調製器的輸出寫為
$$v\left ( t \right )=s\left ( t \right )c\left ( t \right )$$
將$s\left ( t \right )$和$c\left ( t \right )$的值代入上述方程。
$$v\left ( t \right )=\frac{A_mA_c}{2} \cos \left [ 2 \pi \left ( f_c-f_m \right )t \right ] A_c \cos \left ( 2 \pi f_ct \right )$$
$=\frac{A_m{A_{c}}^{2}}{2} \cos\left [ 2 \pi\left ( f_c -f_m \right )t \right ] \cos\left ( 2 \pi f_ct \right )$
$=\frac{A_m{A_{c}}^{2}}{4}\left \{ \cos\left [ 2 \pi\left ( 2f_c-fm \right ) \right ]+ \cos\left ( 2 \pi f_m \right )t \right \}$
$v\left ( t \right )=\frac{A_m{A_{c}}^{2}}{4} \cos\left ( 2 \pi f_mt \right )+\frac{A_m{A_{c}}^{2}}{4} \cos\left [ 2 \pi \left ( 2f_c-f_m \right )t \right ]$
在上式中,第一項是訊息訊號的縮放版本。可以透過將上述訊號透過低通濾波器來提取它。
因此,低通濾波器的輸出為
$$v_0\left ( t \right )=\frac{A_m{A_{c}}^{2}}{4} \cos\left ( 2 \pi f_mt \right )$$
這裡,比例因子為$\frac{{A_{c}}^{2}}{4}$。
我們可以使用相同的框圖來解調具有上邊帶的SSB-SC波。考慮以下具有**上邊帶**的**SSB-SC**波。
$$s\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c+f_m \right )t \right ]$$
本地振盪器的輸出為
$$c\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )$$
我們可以將乘積調製器的輸出寫成
$$v\left ( t \right )=s\left ( t \right )c\left ( t \right )$$
將$s\left ( t \right )$和$c\left ( t \right )$的值代入上述方程。
$$\Rightarrow v\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ]A_c \cos\left ( 2 \pi f_ct \right )$$
$=\frac{A_m{A_{c}}^{2}}{2} \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \cos\left ( 2 \pi f_ct \right )$
$=\frac{A_m{A_{c}}^{2}}{4} \left \{ \cos\left [ 2 \pi\left ( 2f_c+f_m \right )t \right ]+ \cos\left ( 2 \pi f_mt \right ) \right \}$
$v\left ( t \right )=\frac{A_m{A_{c}}^{2}}{4} \cos\left ( 2 \pi f_mt \right )+\frac{A_m{A_{c}}^{2}}{4} \cos \left [ 2 \pi\left ( 2f_c+f_m \right )t \right ]$
在上式中,第一項是訊息訊號的縮放版本。可以透過將上述訊號透過低通濾波器來提取它。
因此,低通濾波器的輸出為
$$v_0\left ( t \right )=\frac{A_m{A_{c}}^{2}}{4} \cos\left ( 2 \pi f_mt \right )$$
這裡,比例因子也是$\frac{{A_{c}}^{2}}{4}$。
因此,在兩種情況下,使用相干檢測器都可以得到相同的解調輸出。
模擬通訊 - VSB-SC調製
在前面的章節中,我們討論了SSB-SC調製和解調。SSB-SC調製訊號只有一個邊帶頻率。理論上,我們可以使用理想的帶通濾波器完全獲得一個邊帶頻率分量。然而,實際上我們可能無法獲得整個邊帶頻率分量。由於此原因,某些資訊會丟失。
為了避免這種損失,選擇了一種介於DSB-SC和SSB-SC之間的折衷技術。這種技術稱為**殘留邊帶抑制載波(VSB-SC)**技術。“殘留”一詞意為“一部分”,名稱由此而來。
**VSB-SC調製**是一種過程,其中一部分訊號(稱為殘留)與一個邊帶一起被調製。VSB-SC波的頻譜如下圖所示。
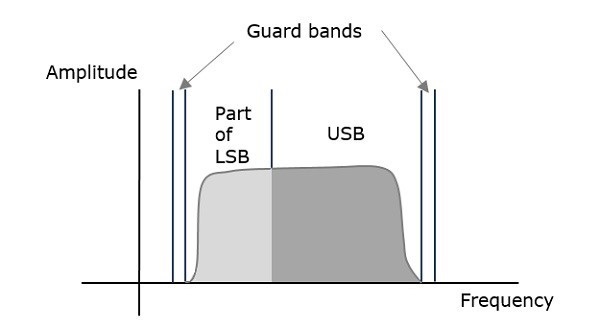
除了上邊帶之外,在此技術中還傳輸了下邊帶的一部分。類似地,我們可以傳輸下邊帶以及上邊帶的一部分。在VSB的兩側設定了一個非常窄的保護帶,以避免干擾。VSB調製主要用於電視傳輸。
VSB-SC調製的頻寬
我們知道SSB-SC調製波的頻寬為$f_m$。由於VSB-SC調製波包含一個邊帶的頻率分量以及另一個邊帶的殘留分量,因此其頻寬將是SSB-SC調製波的頻寬和殘留頻率$f_v$之和。
即,VSB-SC調製波的頻寬 = $f_m + f_v$
優點
以下是VSB-SC調製的優點。
效率高。
與AM和DSB-SC波相比,頻寬減小。
濾波器設計簡單,因為不需要高精度。
可以輕鬆傳輸低頻分量,沒有任何困難。
具有良好的相位特性。
缺點
以下是VSB-SC調製的缺點。
與SSB-SC波相比,頻寬更大。
解調複雜。
應用
VSB-SC最突出和標準的應用是傳輸電視訊號。此外,在考慮頻寬使用時,這也是最方便和有效的方法。
現在,讓我們分別討論生成VSB-SC波的調製器和解調VSB-SC波的解調器。
VSB-SC的產生
VSB-SC波的產生類似於SSB-SC波的產生。VSB-SC調製器如下圖所示。
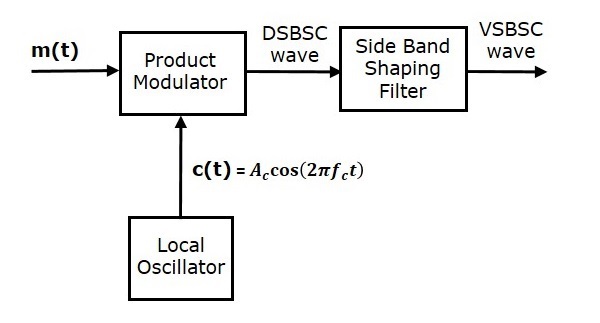
在這種方法中,我們首先在乘積調製器的幫助下生成DSB-SC波。然後,將此DSB-SC波作為邊帶整形濾波器的輸入。該濾波器產生一個輸出,即VSB-SC波。
調製訊號$m\left ( t \right )$和載波訊號$A_c \cos \left ( 2 \pi f_ct \right )$作為輸入應用於乘積調製器。因此,乘積調製器產生一個輸出,它是這兩個輸入的乘積。
因此,乘積調製器的輸出為
$$p\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )m\left ( t \right )$$
在兩邊應用傅立葉變換
$$P\left ( f \right )=\frac{A_c}{2}\left [ M\left ( f-f_c \right )+M\left ( f+f_c \right ) \right ]$$
上述方程表示DSB-SC頻譜的方程。
設邊帶整形濾波器的傳遞函式為$H\left ( f \right )$。該濾波器的輸入為$p\left ( t \right )$,輸出為VSB-SC調製波$s\left ( t \right )$。$p\left ( t \right )$和$s\left ( t \right )$的傅立葉變換分別為$P\left ( t \right )$和$S\left ( t \right )$。
在數學上,我們可以將$S\left ( f \right )$寫成
$$S\left ( t \right )=P\left ( f \right )H\left ( f \right )$$
將$P\left ( f \right )$的值代入上述方程。
$$S\left ( f \right )=\frac{A_c}{2}\left [ M\left ( f-f_c \right )+M\left ( f+f_c \right ) \right ]H\left ( f \right )$$
上述方程表示VSB-SC頻譜的方程。
VSB-SC的解調
VSB-SC波的解調類似於SSB-SC波的解調。這裡,使用相同的載波訊號(用於生成VSB-SC波)來檢測訊息訊號。因此,這種檢測過程稱為**相干**或**同步檢測**。VSB-SC解調器如下圖所示。
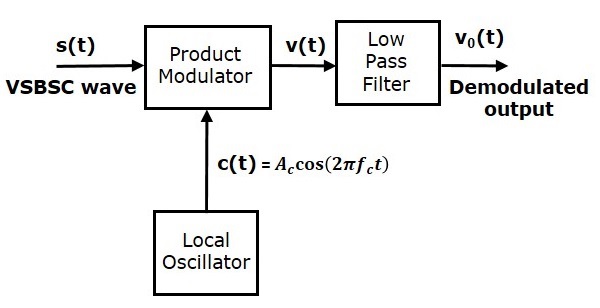
在這個過程中,可以透過將VSB-SC波與具有相同頻率和相位的載波相乘來提取訊息訊號,該載波在VSB-SC調製中使用。然後將得到的訊號透過低通濾波器。該濾波器的輸出是所需的訊息訊號。
設VSB-SC波為$s\left ( t \right )$,載波訊號為$A_c \cos \left ( 2 \pi f_ct \right )$。
從圖中,我們可以將乘積調製器的輸出寫成
$$v\left ( t \right )= A_c \cos\left ( 2 \pi f_ct \right )s\left ( t \right )$$
在兩邊應用傅立葉變換
$$V\left ( f \right )= \frac{A_c}{2}\left [ S\left ( f-f_c \right )+S\left ( f+f_c \right ) \right ]$$
我們知道$S\left ( f \right )=\frac{A_c}{2}\left [ M\left ( f-f_c \right ) + M\left ( f+f_c \right )\right ]H\left ( f \right )$
從上述方程,讓我們找到$S\left ( f-f_c \right )$和$S\left ( f+f_c \right )$。
$$S\left ( f-f_c \right )=\frac{A_c}{2}\left [ M\left ( f-f_c-f_c \right ) + M\left ( f-f_c+f_c \right )\right ]H\left ( f-f_c \right )$$
$\Rightarrow S\left ( f-f_c \right )=\frac{A_c}{2}\left [ M\left ( f-2f_c \right )+M\left ( f \right ) \right ] H\left ( f-f_c \right )$
$$S\left ( f+f_c \right )=\frac{A_c}{2}\left [ M\left ( f+f_c-f_c \right ) +M\left ( f+f_c+f_c \right )\right ] H\left ( f+f_c \right )$$
$\Rightarrow S\left ( f+f_c \right )=\frac{A_c}{2}\left [ M \left ( f \right )+M \left (f+2f_c \right ) \right ] H \left ( f+f_c \right )$
將$S\left ( f-f_c \right )$和$S\left ( f+f_c \right )$的值代入$V\left ( f \right )$。
$V(f) = \frac{A_c}{2}[\frac{A_c}{2}[M(f-2f_c)+M(f)]H(f-f_c)+$
$\frac{A_c}{2}[M(f)+M(f+2f_c)]H(f+f_c)]$
$\Rightarrow V\left ( f \right )=\frac{{A_{c}}^{2}}{4} M\left ( f \right )\left [ H\left ( f-f_c \right )+H \left ( f+f_c \right ) \right ]$
$+ \frac{{A_{c}}^{2}}{4}\left [ M\left ( f-2f_c \right )H\left ( f-f_c \right )+M\left ( f+2f_c \right )H\left ( f+f_c \right ) \right ]$
在上述方程中,第一項表示所需訊息訊號頻譜的縮放版本。可以透過將上述訊號透過低通濾波器來提取它。
$$V_0\left ( f \right )=\frac{{A_{c}}^{2}}{4} M\left ( f \right )\left [ H\left ( f-f_c \right )+H\left ( f+f_c \right ) \right ]$$
模擬通訊 - 角調製
連續波調製中的另一種調製型別是**角調製**。角調製是載波訊號的頻率或相位根據訊息訊號變化的過程。
角調製波的標準方程為
$$s\left ( t \right )=A_c \cos \theta _i\left ( t \right )$$
其中:
$A_c$是調製波的幅度,與載波訊號的幅度相同
$\theta _i\left ( t \right )$是調製波的相位
角調製進一步細分為調頻和相移鍵控。
**調頻**是載波訊號的頻率隨訊息訊號線性變化的過程。
**相移鍵控**是載波訊號的相位隨訊息訊號線性變化的過程。
現在,讓我們詳細討論這些。
調頻
在幅度調製中,載波訊號的幅度發生變化。而在**調頻(FM)**中,載波訊號的頻率根據調製訊號的瞬時幅度變化。
因此,在調頻中,載波訊號的幅度和相位保持不變。可以透過觀察下圖更好地理解這一點。
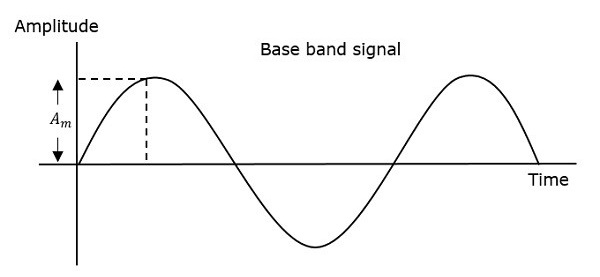

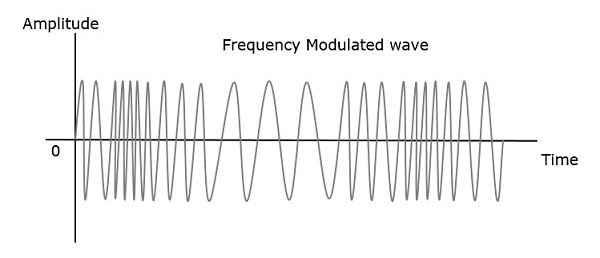
當調製訊號或訊息訊號的幅度增加時,調製波的頻率增加。類似地,當調製訊號的幅度減小,調製波的頻率減小。請注意,當調製訊號的幅度為零時,調製波的頻率保持恆定,並且等於載波訊號的頻率。
數學表示
調頻中瞬時頻率$f_i$的方程為
$$f_i=f_c+k_fm\left ( t \right )$$
其中:
$f_c$是載波頻率
$k_t$是頻率靈敏度
$m\left ( t \right )$是訊息訊號
我們知道角頻率$\omega_i$和角度$\theta _i\left ( t \right )$之間的關係為
$$\omega_i=\frac{d\theta _i\left ( t \right )}{dt}$$
$\Rightarrow 2 \pi f_i=\frac{d\theta _i\left ( t \right )}{dt}$
$\Rightarrow \theta _i\left ( t \right )= 2\pi\int f_i dt$
將 $f_i$ 的值代入上式。
$$\theta _i\left ( t \right )=2 \pi\int \left ( f_c+k_f m\left ( t \right ) \right )dt$$
$\Rightarrow \theta _i\left ( t \right )=2 \pi f_ct+2 \pi k_f\int m\left ( t \right )dt$
將 $\theta _i\left ( t \right )$ 的值代入角調製波的標準方程。
$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct + 2 \pi k_f \int m\left ( t \right )dt \right )$$
這是調頻波的方程。
如果調製訊號為 $m\left ( t \right )= A_m \cos \left ( 2 \pi f_mt \right )$, 則調頻波的方程為
$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct + \beta \sin \left ( 2 \pi f_mt \right ) \right )$$
其中:
$\beta$ = 調頻指數 $=\frac{\Delta f}{f_m}=\frac{k_fA_m}{f_m}$
調頻波頻率(瞬時頻率)與正常載波頻率之間的差異稱為頻偏。用 $\Delta f$ 表示,等於 $k_f$ 和 $A_m$ 的乘積。
根據調頻指數 $\beta$ 的值,可以將調頻分為窄帶調頻和寬頻調頻。
窄帶調頻
以下是窄帶調頻的特點。
與寬頻調頻相比,這種調頻具有較小的頻寬。
調頻指數 $\beta$ 很小,即小於 1。
其頻譜由載波、上邊帶和下邊帶組成。
它用於行動通訊,例如警用無線電、救護車、計程車等。
寬頻調頻
以下是寬頻調頻的特點。
這種調頻具有無限頻寬。
調頻指數 $\beta$ 很大,即大於 1。
其頻譜由載波和無限數量的邊帶組成,這些邊帶位於載波周圍。
它用於娛樂、廣播應用,例如調頻廣播、電視等。
相位調製
在調頻中,載波的頻率發生變化。而在相位調製 (PM) 中,載波訊號的相位根據調製訊號的瞬時幅度發生變化。
因此,在相位調製中,載波訊號的幅度和頻率保持不變。透過觀察下圖可以更好地理解這一點。
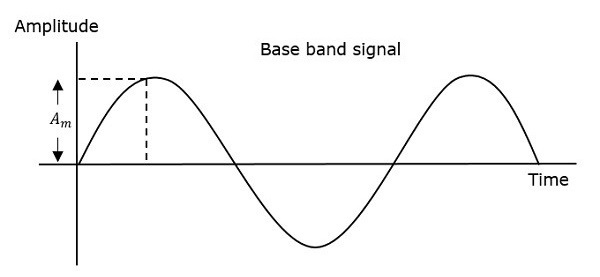
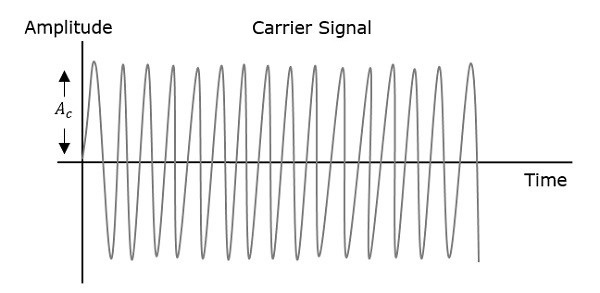

調製波的相位有無限個點,波形可以在這些點發生相移。調製訊號的瞬時幅度改變載波訊號的相位。當幅度為正時,相位在一個方向上變化;如果幅度為負,則相位在相反方向上變化。
數學表示
相位調製中瞬時相位 $\phi_i$ 的方程為
$$\phi _i=k_p m\left ( t \right )$$
其中:
$k_p$ 是相位靈敏度
$m\left ( t \right )$是訊息訊號
角調製波的標準方程為
$$s\left ( t \right )=A_c \cos \left ( 2 \pi f_ct+\phi_i \right )$$
將 $\phi_i$ 的值代入上式。
$$s\left ( t \right )=A_c \cos \left ( 2 \pi f_ct+k_p m \left ( t \right )\right )$$
這是相位調製波的方程。
如果調製訊號 $m\left ( t \right )=A_m \cos \left ( 2 \pi f_mt \right ) $, 則相位調製波的方程為
$$s\left ( t \right )=A_c \cos\left (2 \pi f_ct+\beta \cos\left ( 2 \pi f_mt \right ) \right )$$
其中:
$\beta$ = 調頻指數 = $\Delta \phi=k_pA_m$
$\Delta \phi$ 是相位偏移
相位調製用於移動通訊系統,而調頻主要用於調頻廣播。
數值問題2
在上一章中,我們討論了角調製中使用的引數。每個引數都有自己的公式。透過使用這些公式,我們可以找到相應的引數值。在本章中,讓我們根據調頻的概念解決一些問題。
問題1
幅度為 5 V、頻率為 2 KHz 的正弦調製波形施加到調頻發生器,該發生器的頻率靈敏度為 40 Hz/伏特。計算頻偏、調頻指數和頻寬。
解答
已知調製訊號的幅度 $A_m=5V$
調製訊號的頻率 $f_m=2 KHz$
頻率靈敏度 $k_f=40 Hz/volt$
我們知道頻偏的公式為
$$\Delta f=k_f A_m$$
將 $k_f$ 和 $A_m$ 的值代入上式。
$$\Delta f=40 \times 5=200Hz$$
因此,頻偏 $\Delta f$ 為 $200Hz$
調頻指數的公式為
$$\beta = \frac{\Delta f}{f_m}$$
將 $\Delta f$ 和 $f_m$ 的值代入上式。
$$\beta=\frac{200}{2 \times 1000}=0.1$$
這裡,調頻指數 $\beta$ 的值為 0.1,小於 1。因此,它是窄帶調頻。
窄帶調頻的頻寬公式與調幅波的頻寬公式相同。
$$BW=2f_m$$
將 $f_m$ 的值代入上述公式。
$$BW=2 \times 2K=4KHz$$
因此,窄帶調頻波的頻寬為 $4 KHz$。
問題2
一個調頻波由 $s\left ( t \right )=20 \cos\left ( 8 \pi \times10^6t+9 \sin\left ( 2 \pi \times 10^3 t \right ) \right )$ 給出。計算調頻波的頻偏、頻寬和功率。
解答
已知調頻波的方程為
$$s\left ( t \right )=20 \cos\left ( 8 \pi \times10^6t+9 \sin\left ( 2 \pi \times 10^3 t \right ) \right )$$
我們知道調頻波的標準方程為
$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct + \beta \sin \left ( 2 \pi f_mt \right ) \right )$$
透過比較以上兩個方程,我們將得到以下值。
載波訊號的幅度 $A_c=20V$
載波訊號的頻率 $f_c=4 \times 10^6 Hz=4 MHz$
訊息訊號的頻率 $f_m=1 \times 10^3 Hz = 1KHz$
調頻指數 $\beta=9$
這裡,調頻指數的值大於 1。因此,它是寬頻調頻。
我們知道調製指數的公式為
$$\beta=\frac {\Delta f}{f_m}$$
將上式重新排列如下。
$$\Delta=\beta f_m$$
將 $\beta$ 和 $f_m$ 的值代入上式。
$$\Delta=9 \times 1K =9 KHz$$
因此,頻偏 $\Delta f$ 為 $9 KHz$。
寬頻調頻波頻寬的公式為
$$BW=2\left ( \beta +1 \right )f_m$$
將 $\beta$ 和 $f_m$ 的值代入上式。
$$BW=2\left ( 9 +1 \right )1K=20KHz$$
因此,寬頻調頻波的頻寬為 $20 KHz$
調頻波功率的公式為
$$P_c= \frac{{A_{c}}^{2}}{2R}$$
假設 $R=1\Omega$ 並將 $A_c$ 的值代入上式。
$$P=\frac{\left ( 20 \right )^2}{2\left ( 1 \right )}=200W$$
因此,調頻波的功率為 $200$ 瓦。
模擬通訊 - 調頻調製器
在本章中,讓我們討論一下產生窄帶調頻和寬頻調頻波的調製器。首先,讓我們討論一下窄帶調頻的產生。
窄帶調頻的產生
我們知道調頻波的標準方程為
$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct+2 \pi k_f\int m\left ( t \right ) dt\right )$$
$\Rightarrow s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right ) \cos\left ( 2 \pi k_f\int m\left ( t \right )dt \right )-$
$A_c \sin\left ( 2 \pi f_ct \right ) \sin\left ( 2 \pi k_f\int m\left ( t \right )dt \right )$
對於窄帶調頻,
$$\left | 2 \pi k_f\int m\left ( t \right )dt \right | < < 1$$
我們知道當 $\theta$ 很小時,$\cos \theta \approx 1$ 且 $\sin \theta \approx 1$。
使用上述關係,我們將得到窄帶調頻方程為
$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct \right )-A_c \sin\left ( 2 \pi f_ct \right )2 \pi k_f\int m\left ( t \right )dt$$
窄帶調頻調製器的框圖如下所示。
這裡,積分器用於對調製訊號 $m\left (t \right )$ 進行積分。載波訊號 $A_c \cos \left ( 2 \pi f_ct \right )$ 透過 $-90^0$ 移相器進行 $-90^0$ 移相以獲得 $A_c \sin \left ( 2 \pi f_ct \right )$。乘法調製器有兩個輸入 $\int m\left ( t \right )dt$ 和 $A_c \sin \left ( 2 \pi f_ct \right )$。它產生一個輸出,它是這兩個輸入的乘積。
透過在正向路徑中放置一個 $2 \pi k_f$ 模組,將其進一步乘以 $2 \pi k_f$。加法器模組有兩個輸入,它們正是窄帶調頻方程的兩個項。在加法器模組的輸入端,為載波訊號和其他項分配正負號。最後,加法器模組產生窄帶調頻波。
寬頻調頻的產生
以下兩種方法可以產生寬頻調頻波。
- 直接法
- 間接法
直接法
此方法稱為直接法,因為我們直接生成寬頻調頻波。在這種方法中,電壓控制振盪器 (VCO) 用於生成寬頻調頻。VCO 產生一個輸出訊號,其頻率與輸入訊號電壓成正比。這類似於調頻波的定義。寬頻調頻波生成的框圖如下所示。
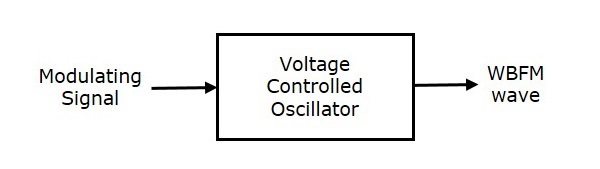
這裡,調製訊號 $m\left (t \right )$ 作為電壓控制振盪器 (VCO) 的輸入。VCO 產生一個輸出,它就是寬頻調頻。
$$f_i \: \alpha \: m\left ( t \right )$$
$$\Rightarrow f_i=f_c+k_fm\left ( t \right )$$
其中:
$f_i$ 是寬頻調頻波的瞬時頻率。
間接法
此方法稱為間接法,因為我們間接生成寬頻調頻波。這意味著,我們首先生成窄帶調頻波,然後藉助倍頻器獲得寬頻調頻波。寬頻調頻波生成的框圖如下所示。
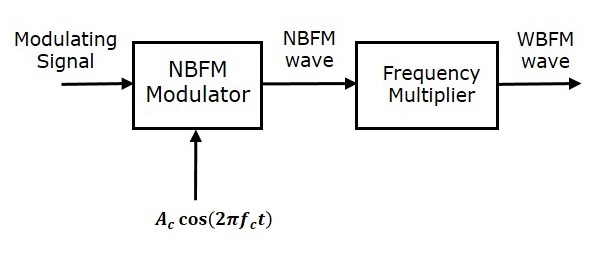
此框圖主要包含兩個階段。在第一階段,將使用窄帶調頻調製器生成窄帶調頻波。我們在本章開頭已經看到了窄帶調頻調製器的框圖。我們知道窄帶調頻波的調頻指數小於 1。因此,為了獲得所需的調頻波調頻指數(大於 1),請正確選擇倍頻器的值。
倍頻器是一種非線性器件,它產生的輸出訊號的頻率是輸入訊號頻率的 n 倍。其中,n 是倍頻因子。
如果將調頻指數 $\beta$ 小於 1 的窄帶調頻波作為倍頻器的輸入,則倍頻器產生的輸出訊號的調頻指數是 $\beta$ 的 n 倍,頻率也是寬頻調頻波頻率的 n 倍。
有時,我們可能需要多個階段的倍頻器和混頻器才能提高調頻波的頻偏和調頻指數。
模擬通訊 - 調頻解調器
在本章中,讓我們討論一下解調調頻波的解調器。以下兩種方法可以解調調頻波。
- 頻率鑑別法
- 相位鑑別法
頻率鑑別法
我們知道調頻波的方程為
$$s\left ( t \right ) =A_c \cos \left ( 2 \pi f_ct+2 \pi k_f \int m\left ( t \right )dt \right )$$
對方程關於 't' 求導。
$$\frac{ds\left ( t \right )}{dt}= -A_c\left ( 2 \pi f_c+2 \pi k_fm\left ( t \right ) \right ) \sin\left ( 2 \pi f_ct+2 \pi k_f\int m\left ( t \right )dt \right )$$
我們可以將$-\sin \theta$寫成$\sin \left ( \theta -180^0 \right )$。
$$\Rightarrow \frac{ds(t)}{dt}=A_c\left ( 2 \pi f_c+2 \pi k_fm\left ( t \right ) \right )\sin\left ( 2 \pi f_ct+2 \pi k_f \int m\left ( t \right )dt-180^0 \right )$$
$$\Rightarrow \frac{ds(t)}{dt}=A_c\left ( 2 \pi f_c \right )\left [ 1+\left ( \frac{k_f}{k_c} \right )m\left ( t \right ) \right ] \sin\left ( 2 \pi f_ct+2 \pi k_f\int m\left ( t \right )dt-180^0 \right )$$
在上式中,幅度項類似於AM波的包絡,相位項類似於FM波的相位。這裡,我們的需求是調製訊號$m\left ( t \right )$。因此,我們可以從AM波的包絡中恢復它。
下圖顯示了使用頻率鑑別方法的FM解調器的框圖。
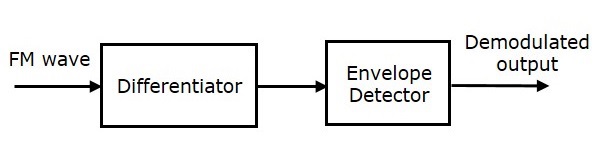
該框圖包括微分器和包絡檢波器。微分器用於將FM波轉換為AM波和FM波的組合。這意味著,它將FM波的頻率變化轉換為AM波相應的電壓(幅度)變化。我們知道包絡檢波器的操作。它產生AM波的解調輸出,也就是調製訊號。
相位鑑別法
下圖顯示了使用相位鑑別方法的FM解調器的框圖。
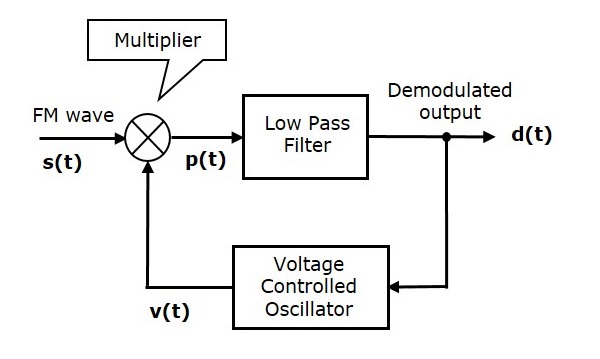
該框圖包括乘法器、低通濾波器和壓控振盪器(VCO)。VCO產生輸出訊號$v \left ( t \right )$,其頻率與輸入訊號電壓$d \left ( t \right )$成正比。最初,當訊號$d \left ( t \right )$為零時,調整VCO以產生輸出訊號$v \left ( t \right )$,其具有載波頻率並且相對於載波訊號具有$-90^0$相移。
FM波$s \left ( t \right )$和VCO輸出$v \left ( t \right )$作為乘法器的輸入。乘法器產生一個輸出,該輸出具有高頻分量和低頻分量。低通濾波器消除高頻分量,只產生低頻分量作為其輸出。
此低頻分量僅包含與相位差相關的項。因此,我們從低通濾波器的此輸出中獲得調製訊號$m \left ( t \right )$。
模擬通訊 - 多路複用
多路複用是將多個訊號組合成一個訊號,透過共享介質傳輸的過程。如果複用的是模擬訊號,則稱為模擬多路複用。類似地,如果複用的是數字訊號,則稱為數字多路複用。
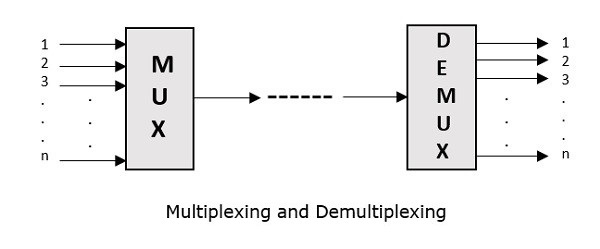
多路複用最初是在電話中開發的。將許多訊號組合起來透過一根電纜傳送。多路複用過程將通訊通道劃分為多個邏輯通道,為每個通道分配不同的訊息訊號或要傳輸的資料流。執行多路複用的裝置可以稱為多路複用器或MUX。
反向過程,即從一個訊號中提取多個通道,在接收端完成,稱為多路分解。執行多路分解的裝置可以稱為多路分解器或DEMUX。
下圖說明了MUX和DEMUX的概念。它們主要用於通訊領域。
多路複用器的型別
多路複用器主要有兩種型別:模擬和數字。它們進一步細分為頻分多路複用(FDM)、波分多路複用(WDM)和時分多路複用(TDM)。下圖詳細介紹了這種分類。
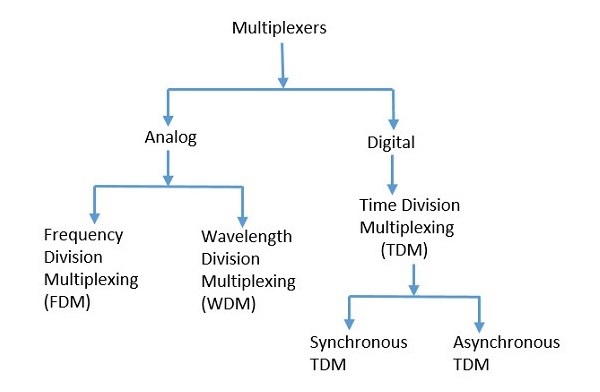
有多種多路複用技術。其中,我們在上圖中提到了具有通用分類的主要型別。讓我們分別看一下它們。
模擬多路複用
模擬多路複用技術中使用的訊號本質上是模擬的。模擬訊號根據其頻率(FDM)或波長(WDM)進行復用。
頻分多路複用
在模擬多路複用中,最常用的技術是頻分多路複用(FDM)。該技術使用不同的頻率來組合資料流,以便將它們作為單個訊號傳送到通訊介質上。
示例 - 透過一根電纜傳送多個頻道的傳統電視發射機使用FDM。
波分多路複用
波分多路複用(WDM)是一種模擬技術,其中許多不同波長的資料流在光譜中傳輸。如果波長增加,則訊號頻率降低。稜鏡可以將不同的波長轉換為單行,可以在MUX的輸出端和DEMUX的輸入端使用。
示例 - 光纖通訊使用WDM技術,將不同的波長合併成單束光進行通訊。
數字多路複用
術語“數字”表示離散的資訊位。因此,可用資料以幀或資料包的形式存在,它們是離散的。
時分多路複用
在時分多路複用(TDM)中,時間幀被劃分為時隙。該技術用於透過分配每個訊息一個時隙,在單個通訊通道上傳輸訊號。
時分多路複用(TDM)可以分為同步TDM和非同步TDM。
同步TDM
在同步TDM中,輸入連線到一個幀。如果有“n”個連線,則將幀劃分為“n”個時隙。每個輸入線路分配一個時隙。
在這種技術中,所有訊號的取樣率都是相同的,因此提供相同的時鐘輸入。MUX始終為每個裝置分配相同的時隙。
非同步TDM
在非同步TDM中,每個訊號的取樣率不同,不需要公共時鐘。如果為某個時隙分配的裝置沒有傳輸任何內容並且處於空閒狀態,則可以將該時隙分配給另一個裝置,這與同步TDM不同。
這種型別的TDM用於非同步傳輸模式網路。
多路分解器
多路分解器用於將單個源連線到多個目的地。此過程是多路複用的逆過程。如前所述,它主要用於接收器。DEMUX有許多應用。它用於通訊系統中的接收器。它用於計算機中的算術邏輯單元以提供電源和傳遞通訊等。
多路分解器用作序列到並行轉換器。序列資料作為輸入定期提供給DEMUX,並且連線了一個計數器來控制多路分解器的輸出。
多路複用器和多路分解器在通訊系統中都發揮著重要作用,分別在發射機和接收機部分。
模擬通訊 - 噪聲
在任何通訊系統中,在訊號傳輸過程中或接收訊號時,都會有一些不需要的訊號進入通訊,使接收器感到不愉快,並質疑通訊的質量。這種干擾稱為噪聲。
什麼是噪聲?
噪聲是不需要的訊號,它會干擾原始訊息訊號並破壞訊息訊號的引數。通訊過程中的這種改變會導致訊息被更改。它很可能在通道或接收器處進入。
可以透過檢視下圖來了解噪聲訊號。
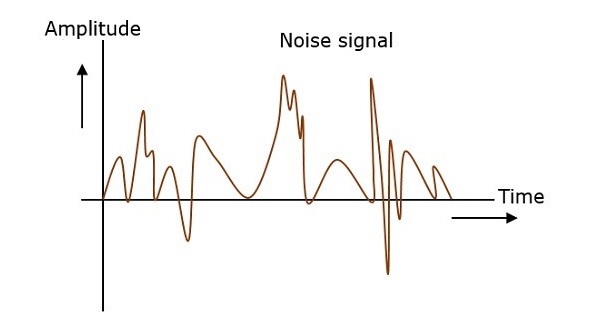
因此,可以理解噪聲是一些沒有規律且沒有恆定頻率或幅度的訊號。它非常隨機且不可預測。通常會採取措施來減少它,儘管它無法完全消除。
噪聲最常見的例子是 -
收音機中的嘶嘶聲
電話交談中的嗡嗡聲
電視機中的閃爍等
噪聲的型別
噪聲的分類取決於源的型別、它表現出的影響或它與接收器之間的關係等。
噪聲產生的兩種主要方式。一種是透過一些外部源,另一種是在接收器部分內部由內部源產生。
外部源
這種噪聲是由外部源產生的,通常會發生在通訊的介質或通道中。這種噪聲無法完全消除。最好的方法是避免噪聲影響訊號。
例子
這種型別噪聲最常見的例子是
大氣噪聲(由於大氣的不規則性)。
地外噪聲,例如太陽噪聲和宇宙噪聲。
工業噪聲。
內部源
這種噪聲是由接收器元件在工作時產生的。電路中的元件由於持續工作可能會產生幾種型別的噪聲。這種噪聲是可量化的。適當的接收器設計可以降低這種內部噪聲的影響。
例子
這種型別噪聲最常見的例子是
熱騷動噪聲(約翰遜噪聲或電噪聲)
散粒噪聲(由於電子和空穴的隨機運動)
傳輸時間噪聲(在過渡期間)
雜項噪聲是另一種型別的噪聲,包括閃爍、電阻效應和混頻器產生的噪聲等。
噪聲的影響
噪聲是一個不方便的特性,會影響系統性能。以下是噪聲的影響。
噪聲限制了系統的操作範圍
噪聲間接地限制了放大器可以放大的最弱訊號。混頻器電路中的振盪器由於噪聲可能會限制其頻率。系統的執行取決於其電路的執行。噪聲限制了接收器能夠處理的最小訊號。
噪聲影響接收器的靈敏度
靈敏度是獲得指定質量輸出所需的最小輸入訊號量。噪聲會影響接收器系統的靈敏度,最終會影響輸出。
模擬通訊 - 信噪比計算
在本章中,讓我們計算各種調製波的信噪比和品質因數,這些調製波在接收器處解調。
信噪比
信噪比(SNR)是訊號功率與噪聲功率之比。SNR值越高,接收到的輸出質量越好。
可以使用以下公式計算不同點的信噪比。
輸入SNR = $\left ( SNR \right )_I= \frac{調製訊號的平均功率}{輸入噪聲的平均功率}$
輸出SNR = $\left ( SNR \right )_O= \frac{解調訊號的平均功率}{輸出噪聲的平均功率}$
通道SNR = $\left ( SNR \right )_C= \frac{調製訊號的平均功率}{訊息頻寬中噪聲的平均功率}$
品質因數
輸出SNR與輸入SNR之比可以稱為品質因數。用F表示。它描述了裝置的效能。
$$F=\frac {\left ( 信噪比 \right )_O}{\left ( 信噪比 \right )_I}$$
接收機的品質因數為
$$F=\frac {\left ( 信噪比 \right )_O}{\left ( 信噪比 \right )_C}$$
這是因為對於接收機來說,通道是輸入。
AM系統中的信噪比計算
考慮以下AM系統的接收機模型來分析噪聲。

我們知道調幅(AM)波為
$$s\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )$$
$$\Rightarrow s\left ( t \right )=A_c \cos \left ( 2 \pi f_ct \right )+A_ck_am\left ( t \right ) \cos\left ( 2 \pi f_ct \right )$$
AM波的平均功率為
$$P_s=\left ( \frac{A_c}{\sqrt{2}} \right )^2+\left ( \frac{A_ck_am\left ( t \right )}{\sqrt{2}} \right )^2=\frac{{A_{c}}^{2}}{2}+\frac{{A_{c}}^{2}{k_{a}}^{2}P}{2}$$
$$\Rightarrow P_s=\frac{{A_{c}}^{2}\left ( 1+{k_{a}}^{2}P \right )}{2}$$
訊息頻寬內噪聲的平均功率為
$$P_{nc}=WN_0$$
將這些值代入**通道信噪比**公式
$$\left ( 信噪比 \right )_{C,AM}=\frac{AM波的平均功率}{訊息頻寬內噪聲的平均功率}$$
$$\Rightarrow \left ( 信噪比 \right )_{C,AM}=\frac{{A_{c}}^{2}\left ( 1+ {k_{a}}^{2}\right )P}{2WN_0}$$
其中:
**P**為訊息訊號的功率=$\frac{{A_{m}}^{2}}{2}$
**W**為訊息頻寬
假設帶通噪聲與通道中的AM波混合,如上圖所示。這種組合應用於AM解調器的輸入。因此,AM解調器的輸入為。
$$v\left ( t \right )=s\left ( t \right )+n\left ( t \right )$$
$\Rightarrow v\left ( t \right )=A_c\left [ 1+k_am\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )+$
$\left [ n_1\left ( t \right ) \cos\left ( 2 \pi f_ct \right ) - n_Q\left ( t \right ) \sin \left ( 2 \pi f_ct \right )\right ]$
$\Rightarrow v\left ( t \right )=\left [ A_c+A_ck_am\left ( t \right )+n_1\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right )$
其中$n_I \left ( t \right )$和$n_Q \left ( t \right )$是噪聲的同相和正交相位分量。
AM解調器的輸出就是上述訊號的包絡。
$$d\left ( t \right )=\sqrt{\left [ A_c+A_cK_am\left ( t \right )+n_I\left ( t \right ) \right ]^2+\left ( n_Q\left ( t \right ) \right )^2}$$
$$\Rightarrow d\left ( t \right )\approx A_c+A_ck_am\left ( t \right )+n_1\left ( t \right )$$
解調訊號的平均功率為
$$P_m=\left ( \frac{A_ck_am\left ( t \right )}{\sqrt{2}} \right )^2=\frac{{A_{c}}^{2}{k_{a}}^{2}P}{2}$$
輸出噪聲的平均功率為
$$P_no=WN_0$$
將這些值代入**輸出信噪比**公式。
$$\left ( 信噪比 \right )_{O,AM}= \frac {解調訊號的平均功率}{輸出噪聲的平均功率}$$
$$\Rightarrow \left ( 信噪比 \right )_{O,AM}=\frac{{A_{c}}^{2}{k_{a}}^{2}P}{2WN_0}$$
將這些值代入AM接收機的**品質因數**公式。
$$F=\frac{\left ( 信噪比 \right )_{O,AM}}{\left ( 信噪比 \right )_{C,AM}}$$
$$\Rightarrow F=\left ( \frac{{A_{c}^{2}}{k_{a}^{2}}P}{2WN_0} \right )/\left ( \frac{{A_{c}}^{2}\left ( 1+ {k_{a}}^{2}\right )P}{2WN_0} \right )$$
$$\Rightarrow F=\frac{{K_{a}}^{2}P}{1+{K_{a}}^{2}P}$$
因此,AM接收機的品質因數小於1。
DSBSC系統中的信噪比計算
考慮以下DSBSC系統的接收機模型來分析噪聲。
我們知道DSBSC調製波為
$$s\left ( t \right )=A_cm\left ( t \right ) \cos\left ( 2 \pi f_ct \right )$$
DSBSC調製波的平均功率為
$$P_s=\left ( \frac{A_cm\left ( t \right )}{\sqrt{2}} \right )^2=\frac{{A_{c}}^{2}P}{2}$$
訊息頻寬內噪聲的平均功率為
$$P_{nc}=WN_0$$
將這些值代入**通道信噪比**公式。
$$\left ( 信噪比 \right )_{C,DSBSC}=\frac{DSBSC調製波的平均功率}{訊息頻寬內噪聲的平均功率}$$
$$\Rightarrow \left ( 信噪比 \right )_{C,DSBSC}=\frac{{A_{c}}^{2}P}{2WN_0}$$
假設帶通噪聲與通道中的DSBSC調製波混合,如上圖所示。這種組合作為乘法調製器的一個輸入。因此,此乘法調製器的輸入為
$$v_1\left ( t \right )=s\left ( t \right )+n\left ( t \right )$$
$$\Rightarrow v_1\left ( t \right )=A_cm\left ( t \right ) \cos \left ( 2 \pi f_ct \right )+\left [ n_I\left ( t \right ) \cos\left ( 2 \pi f_ct \right ) - n_Q\left ( t \right ) \sin \left ( 2 \pi f_ct \right )\right ]$$
$$\Rightarrow v_1\left ( t \right )=\left [ A_cm \left ( t \right ) +n_I\left ( t \right ) \right ] \cos\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right )$$
本地振盪器產生載波訊號$c\left ( t \right )= \cos\left ( 2 \pi f_ct \right )。該訊號作為乘法調製器的另一個輸入。因此,乘法調製器產生一個輸出,它是$v_1\left ( t \right )$和$c\left ( t \right )$的乘積。
$$v_2\left ( t \right )= v_1\left ( t \right )c\left ( t \right )$$
將$v_1\left ( t \right )$和$c\left ( t \right )$的值代入上式。
$$\Rightarrow v_2\left ( t \right )=\left ( \left [ A_cm\left ( t \right ) + n_I\left ( t \right )\right ] \cos\left ( 2 \pi f_ct \right )- n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right ) \right ) \cos\left ( 2 \pi f_ct \right )$$
$$\Rightarrow v_2\left ( t \right )=\left [ A_c m\left ( t \right )+n_I\left ( t \right ) \right ] \cos^2\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right ) \cos\left ( 2 \pi f_ct \right )$$
$$\Rightarrow v_2\left ( t \right )=\left [ A_c m\left ( t \right )+n_I\left ( t \right ) \right ] \left ( \frac{1+ \cos\left ( 4 \pi f_ct \right )}{2} \right ) -n_Q\left ( t \right )\frac{ \sin\left ( 4 \pi f_ct \right )}{2}$$
當上述訊號作為低通濾波器的輸入時,我們將得到低通濾波器的輸出為
$$d\left ( t \right )=\frac{\left [ A_c m\left ( t \right )+n_I\left ( t \right ) \right ]}{2}$$
解調訊號的平均功率為
$$P_m=\left ( \frac{A_cm\left ( t \right )}{2\sqrt{2}} \right )^2=\frac{{A_{c}}^{2}P}{8}$$
輸出噪聲的平均功率為
$$P_{no}=\frac{WN_0}{4}$$
將這些值代入**輸出信噪比**公式。
$$\left ( 信噪比 \right )_{O,DSBSC}= \frac {解調訊號的平均功率}{輸出噪聲的平均功率}$$
$$\Rightarrow \left ( 信噪比 \right )_{O,DSBSC}=\left ( \frac{{A_{c}}^{2}P}{8} \right )/ \left ( \frac{WN_0}{4} \right )=\frac{{A_{c}}^{2}P}{2WN_0}$$
將這些值代入DSBSC接收機的**品質因數**公式。
$$F=\frac{\left ( 信噪比 \right )_{O,DSBSC}}{\left ( 信噪比 \right )_{C,DSBSC}}$$
$$\Rightarrow F= \left ( \frac{{A_{c}}^{2}P}{2WN_0} \right )/ \left ( \frac{{A_{c}}^{2}P}{2WN_0} \right )$$
$$\Rightarrow F= 1$$
因此,DSBSC接收機的品質因數為1。
SSBSC系統中的信噪比計算
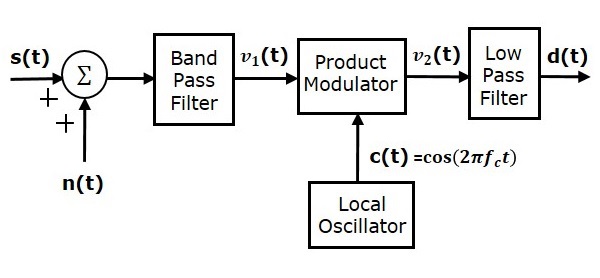
考慮以下SSBSC系統的接收機模型來分析噪聲。
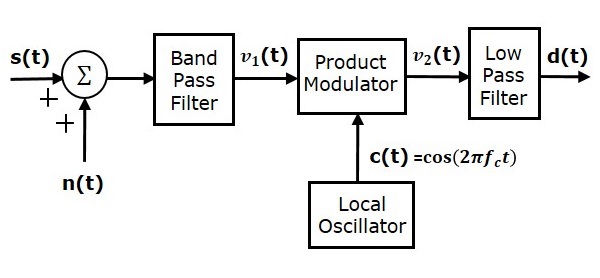
我們知道具有下邊帶的SSBSC調製波為
$$s\left ( t \right )=\frac{A_mA_c}{2} \cos \left [ 2 \pi\left ( f_c-f_m \right )t \right ]$$
SSBSC調製波的平均功率為
$$P_s=\left ( \frac{A_mA_c}{2\sqrt{2}} \right )^2=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8}$$
訊息頻寬內噪聲的平均功率為
$$P_{nc}=WN_0$$
將這些值代入**通道信噪比**公式。
$$\left ( 信噪比 \right )_{C,SSBSC}= \frac {SSBSC調製波的平均功率}{訊息頻寬內噪聲的平均功率}$$
$$\Rightarrow \left ( 信噪比 \right )_{C,SSBSC}=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8WN_0}$$
假設帶通噪聲與通道中的SSBSC調製波混合,如上圖所示。這種組合作為乘法調製器的一個輸入。因此,此乘法調製器的輸入為
$$v_1\left ( t \right )=s\left ( t \right )+n\left ( t \right )$$
$$v_1\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c-f_m \right )t \right ] + n_I\left ( t \right ) \cos\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin \left ( 2 \pi f_ct \right )$$
本地振盪器產生載波訊號$c\left ( t \right )= \cos \left ( 2 \pi f_ct \right )。該訊號作為乘法調製器的另一個輸入。因此,乘法調製器產生一個輸出,它是$v_1\left ( t \right )$和$c\left ( t \right )$的乘積。
$$v_2\left ( t \right )=v_1\left ( t \right )c \left ( t \right )$$
將$v_1\left ( t \right )$和$ c\left ( t \right )$的值代入上式。
$\Rightarrow v_2(t)= (\frac{A_mA_c}{2} \cos[ 2 \pi ( f_c-f_m )t ] + n_I ( t ) \cos ( 2 \pi f_ct )-$
$n_Q( t ) \sin ( 2 \pi f_ct ) )\cos ( 2 \pi f_ct )$
$\Rightarrow v_2\left ( t \right )=\frac{A_mA_c}{2} \cos\left [ 2 \pi \left ( f_c-f_m \right )t \right ] \cos\left ( 2 \pi f_ct \right )+$
$n_I\left ( t \right ) \cos^2\left ( 2 \pi f_ct \right )-n_Q\left ( t \right ) \sin\left ( 2 \pi f_ct \right ) \cos\left ( 2 \pi f_ct \right )$
$\Rightarrow v_2\left ( t \right )=\frac{A_mA_c}{4} \left \{ \cos\left [ 2 \pi\left ( 2f_c-f_m \right )t \right ] + \cos \left ( 2 \pi f_mt \right )\right \}+$
$n_I\left ( t \right )\left ( \frac{1+ \cos\left ( 4 \pi f_ct \right )}{2} \right )- n_Q\left ( t \right )\frac{\sin \left ( 4 \pi f_ct \right )}{2}$
當上述訊號作為低通濾波器的輸入時,我們將得到低通濾波器的輸出為
$$d\left ( t \right )=\frac{A_mA_c}{2} \cos\left ( 2 \pi f_mt \right )+\frac{n_I\left ( t \right )}{2}$$
解調訊號的平均功率為
$$P_m=\left ( \frac{A_mA_c}{4\sqrt{2}} \right )^2=\frac{{A_{m}}^{2}{A_{c}}^{2}}{32}$$
輸出噪聲的平均功率為
$$P_{no}=\frac{WN_0}{4}$$
將這些值代入**輸出信噪比**公式
$$\left ( 信噪比 \right )_{O,SSBSC}= \frac {解調訊號的平均功率}{輸出噪聲的平均功率}$$
$$\Rightarrow \left ( 信噪比 \right )_{O,SSBSC}= \left ( \frac{{A_{m}}^{2}{A_{c}}^{2}}{32} \right )/\left ( \frac{WN_0}{4} \right )=\frac{{A_{m}}^{2}{A_{c}}^{2}}{8WN_0}$$
將這些值代入SSBSC接收機的**品質因數**公式
$$F=\frac{\left ( 信噪比 \right )_{O,SSBSC}}{\left ( 信噪比 \right )_{C,SSBSC}}$$
$$F=\left ( \frac{{A_{m}}^{2}{A_{c}}^{2}}{8WN_0} \right )/\left ( \frac{{A_{m}}^{2}{A_{c}}^{2}}{8WN_0} \right )$$
$$F=1$$
因此,SSBSC接收機的品質因數為1。
模擬通訊 - 發射機
發射機部分末端的天線發射調製波。在本章中,我們將討論AM和FM發射機。
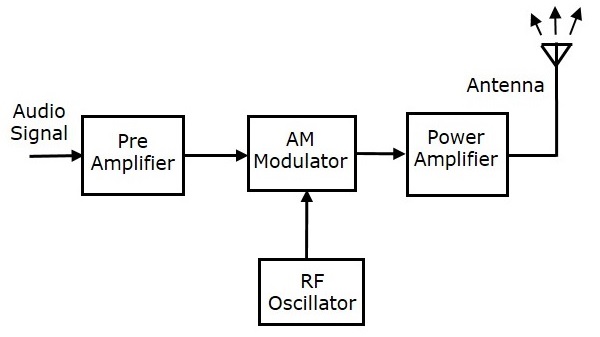
AM發射機
AM發射機以音訊訊號作為輸入,並將幅度調製波傳遞到天線作為輸出進行傳輸。AM發射機的框圖如下所示。
AM發射機的工作原理如下。
來自麥克風輸出的音訊訊號傳送到前置放大器,前置放大器提升調製訊號的電平。
射頻振盪器產生載波訊號。
調製訊號和載波訊號都發送到AM調製器。
功率放大器用於增加AM波的功率電平。此波最終傳遞到天線進行傳輸。
FM發射機
FM發射機是整個單元,它以音訊訊號作為輸入,並將FM波傳遞到天線作為輸出進行傳輸。FM發射機的框圖如下所示。
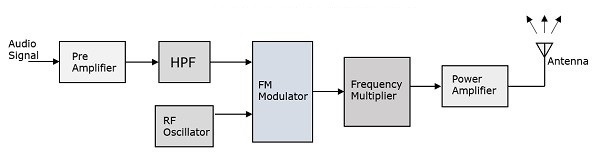
FM發射機的工作原理如下。
來自麥克風輸出的音訊訊號傳送到前置放大器,前置放大器提升調製訊號的電平。
然後將此訊號傳遞到高通濾波器,該濾波器充當預加重網路,以濾除噪聲並提高信噪比。
此訊號進一步傳遞到FM調製器電路。
振盪器電路產生高頻載波,該載波與調製訊號一起傳送到調製器。
使用幾個頻率倍增級來提高工作頻率。即使這樣,訊號的功率也不足以傳輸。因此,最後使用射頻功率放大器來增加調製訊號的功率。此FM調製輸出最終傳遞到天線進行傳輸。
模擬通訊 - 接收機
接收機部分開頭的接收天線接收調製波。首先讓我們討論接收機的要求。
接收機的要求
AM接收機接收AM波並使用包絡檢波器進行解調。類似地,FM接收機接收FM波並使用頻率鑑別方法進行解調。以下是AM和FM接收機的要求。
它應該具有成本效益。
它應該接收相應的調製波。
接收機應該能夠調諧和放大所需的電臺。
它應該能夠抑制不需要的電臺。
必須對所有電臺訊號進行解調,無論載波訊號頻率如何。
為了滿足這些要求,調諧器電路和混頻器電路應該非常有效。射頻混頻的過程是一個有趣的現象。
射頻混頻
射頻混頻單元開發了一個**中頻**(IF),將任何接收到的訊號轉換為該中頻,以便有效地處理訊號。
射頻混頻器是接收機中的一個重要階段。採用兩個不同頻率的訊號,其中一個訊號電平影響另一個訊號的電平,以產生最終的混合輸出。輸入訊號和最終的混頻器輸出在以下圖中進行了說明。
假設第一個和第二個訊號頻率分別為$f_1$和$f_2$。如果將這兩個訊號作為射頻混頻器的輸入,則它會產生一個輸出訊號,該訊號的頻率為$f_1+f_2$和$f_1-f_2$。
如果在頻域中觀察,則模式如下所示。
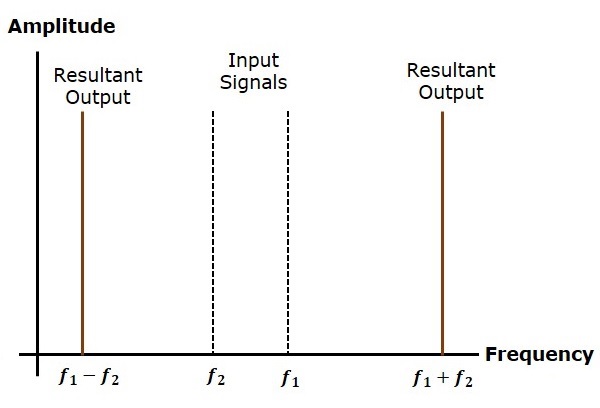
在這種情況下,$f_1$大於$f_2$。因此,最終輸出的頻率為$f_1+f_2$和$f_1-f_2$。類似地,如果$f_2$大於$f_1$,則最終輸出的頻率將為$f_1+f_2$和$f_1-f_2$。
AM接收機
AM超外差接收機以幅度調製波作為輸入,併產生原始音訊訊號作為輸出。**選擇性**是選擇特定訊號同時抑制其他訊號的能力。**靈敏度**是在最低功率電平下檢測射頻訊號並進行解調的能力。
無線電愛好者是最早的無線電接收機。但是,它們存在一些缺點,例如靈敏度和選擇性差。為了克服這些缺點,發明了**超外差**接收機。AM接收機的框圖如下所示。
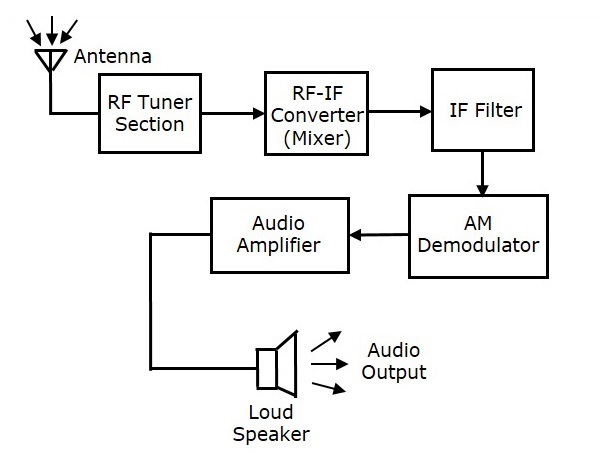
射頻調諧器部分
天線接收到的幅度調製波首先透過變壓器傳遞到**調諧器電路**。調諧器電路只不過是一個LC電路,也稱為**諧振**或**儲能電路**。它選擇AM接收機所需的頻率。它也同時調諧本地振盪器和射頻濾波器。
射頻混頻器
調諧器輸出的訊號傳送到**射頻-中頻轉換器**,該轉換器充當混頻器。它有一個本地振盪器,產生恆定的頻率。這裡完成了混頻過程,接收訊號作為一種輸入,本地振盪器頻率作為另一種輸入。最終輸出是兩種頻率$\left [ \left ( f_1+f_2 \right ) , \left ( f_1-f_2 \right )\right ]$的混合,由混頻器產生,稱為**中頻(IF)**。
中頻的產生有助於解調任何具有任何載波頻率的電臺訊號。因此,所有訊號都被轉換為固定的載波頻率以獲得足夠的選頻性。
中頻濾波器
中頻濾波器是一個帶通濾波器,它透過所需的頻率。它消除了其中存在的所有其他不需要的頻率分量。這是中頻濾波器的優勢,它只允許中頻頻率透過。
AM解調器
現在使用AM解調器對接收到的AM波進行解調。此解調器使用包絡檢波過程來接收調製訊號。
音訊放大器
這是功率放大級,用於放大檢測到的音訊訊號。處理後的訊號得到增強以使其有效。此訊號傳遞到揚聲器以獲得原始聲音訊號。
FM接收機
FM接收機的框圖如下所示。
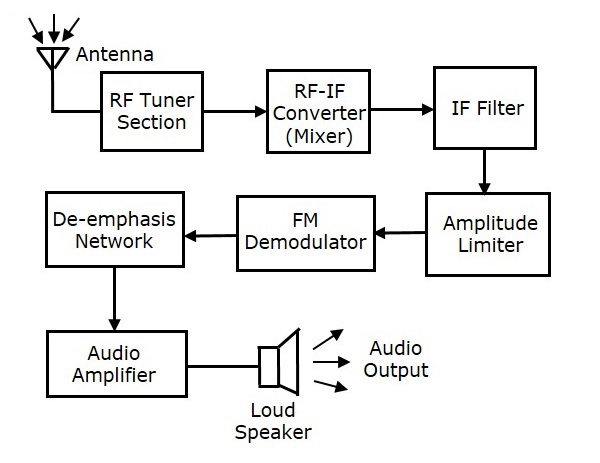
此FM接收機的框圖類似於AM接收機的框圖。兩個模組幅度限制器和去加重網路分別包含在FM解調器之前和之後。其餘模組的操作與AM接收機相同。
我們知道,在FM調製中,FM波的幅度保持恆定。但是,如果在通道中將某些噪聲新增到FM波中,則由於該噪聲,FM波的幅度可能會發生變化。因此,藉助**幅度限制器**,我們可以透過去除噪聲訊號的不需要的峰值來保持FM波的幅度恆定。
在FM發射機中,我們已經看到了預加重網路(高通濾波器),它位於FM調製器之前。這用於提高高頻音訊訊號的信噪比。預加重的反向過程稱為**去加重**。因此,在此FM接收機中,去加重網路(低通濾波器)包含在FM解調器之後。此訊號傳遞到音訊放大器以提高功率電平。最後,我們從揚聲器獲得原始聲音訊號。
模擬通訊 - 取樣
到目前為止,我們已經討論了連續波調製。我們將在下一章討論脈衝調製。這些脈衝調製技術處理離散訊號。因此,現在讓我們看看如何將連續時間訊號轉換為離散訊號。
將連續時間訊號轉換為等效離散時間訊號的過程可以稱為**取樣**。在取樣過程中,會連續取樣某個時刻的資料。
下圖顯示了一個連續時間訊號**x(t)**和相應的取樣訊號**xs(t)**。當**x(t)**乘以週期性脈衝序列時,將獲得取樣訊號**xs(t)**。
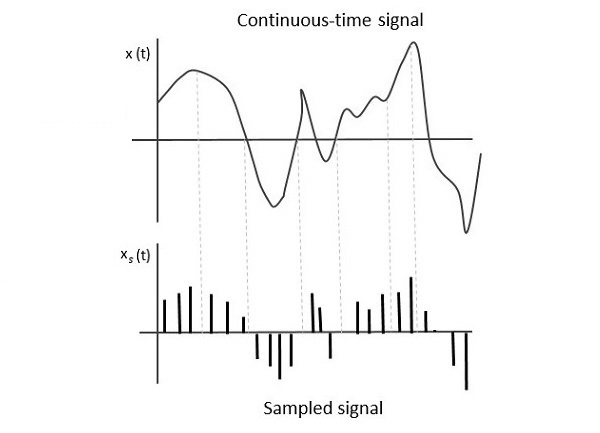
**取樣訊號**是週期性脈衝序列,具有單位幅度,以相等的時間間隔$T_s$進行取樣,稱為**取樣時間**。此資料在時間點$T_s$傳輸,載波訊號在其餘時間傳輸。
取樣率
為了離散化訊號,樣本之間的間隙應該固定。該間隙可以稱為取樣週期$T_s$。取樣週期的倒數稱為**取樣頻率**或**取樣率$f_s$**。
在數學上,我們可以寫成
$$f_s= \frac{1}{T_s}$$
其中:
$f_s$是取樣頻率或採樣率
$T_s$是取樣週期
取樣定理
取樣率應使訊息訊號中的資料既不會丟失,也不會重疊。**取樣定理**指出,“如果以大於或等於給定訊號**W**的最大頻率的兩倍的速率$f_s$進行取樣,則可以精確地重現訊號。”
在數學上,我們可以寫成
$$f_s\geq 2W$$
其中:
$f_s$是取樣率
$W$是給定訊號的最高頻率
如果取樣率等於給定訊號W的最大頻率的兩倍,則稱為**奈奎斯特率**。
取樣定理,也稱為**奈奎斯特定理**,根據頻寬為頻帶受限的函式類提供足夠取樣率的理論。
對於連續時間訊號**x(t)**,其在頻域中頻帶受限,表示如下所示。
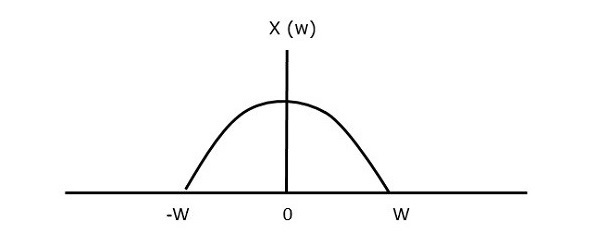
如果訊號以高於奈奎斯特率的速率進行取樣,則可以恢復原始訊號。下圖說明了訊號,如果在頻域中以高於**2w**的速率進行取樣。
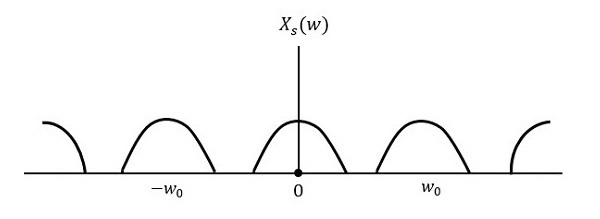
如果以低於**2w**的速率對同一訊號進行取樣,則取樣訊號將如下所示。
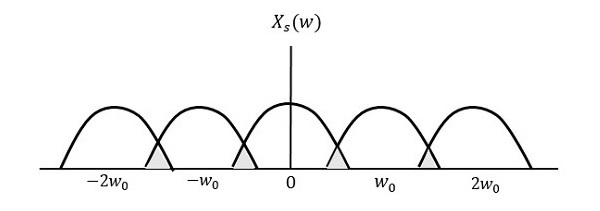
我們可以從上述模式中觀察到,資訊存在重疊,這會導致資訊混合和丟失。這種不需要的重疊現象稱為**混疊**。
混疊可以指“訊號頻譜中的高頻分量在取樣版本的頻譜中呈現低頻分量身份的現象。”
因此,訊號的取樣率選擇為奈奎斯特率。如果取樣率等於給定訊號**W**的最高頻率的兩倍,則取樣訊號將如下所示。
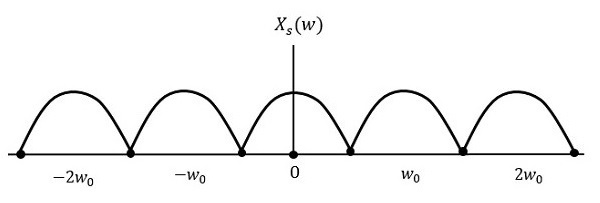
在這種情況下,訊號可以在沒有任何損失的情況下恢復。因此,這是一個良好的取樣率。
模擬通訊 - 脈衝調製
在連續波調製之後,下一個分類是脈衝調製。在本章中,讓我們討論以下模擬脈衝調製技術。
- 脈衝幅度調製
- 脈衝寬度調製
- 脈衝位置調製
脈衝幅度調製
在**脈衝幅度調製 (PAM)** 技術中,脈衝載波的幅度發生變化,該變化與訊息訊號的瞬時幅度成正比。
脈衝幅度調製訊號將跟隨原始訊號的幅度,因為訊號描繪了整個波形的路徑。在自然 PAM 中,可以透過一個具有精確截止頻率的有效**低通濾波器 (LPF)**,將以奈奎斯特速率取樣的訊號重建。
下圖解釋了脈衝幅度調製。

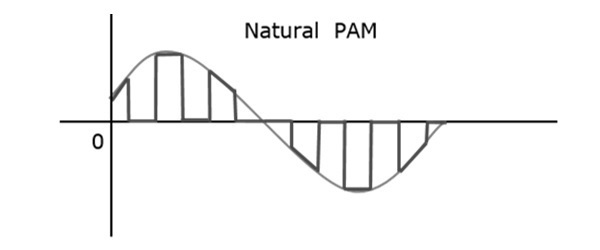
儘管 PAM 訊號通過了 LPF,但它無法在不失真的情況下恢復訊號。因此,為了避免這種噪聲,請使用平頂取樣。平頂 PAM 訊號顯示在下圖中。

**平頂取樣**是一個過程,其中,被取樣訊號可以用脈衝表示,對於這些脈衝,訊號的幅度不能相對於要取樣的模擬訊號發生變化。幅度的頂部保持平坦。此過程簡化了電路設計。
脈衝寬度調製
在**脈衝寬度調製 (PWM)** 或脈衝持續時間調製 (PDM) 或脈衝時間調製 (PTM) 技術中,脈衝載波的寬度或持續時間或時間發生變化,該變化與訊息訊號的瞬時幅度成正比。
在這種方法中,脈衝的寬度會發生變化,但訊號的幅度保持不變。幅度限制器用於使訊號的幅度保持恆定。這些電路將幅度裁剪到所需的水平,因此噪聲受到限制。
下圖解釋了脈衝寬度調製的型別。
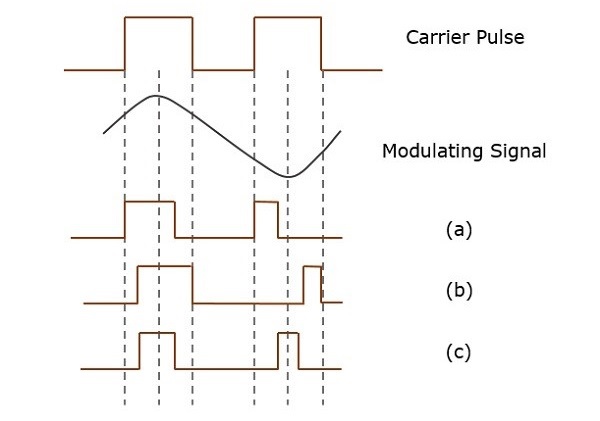
PWM 有三種類型。
脈衝的前沿保持恆定,後沿根據訊息訊號變化。此類 PWM 的波形在上圖中表示為 (a)。
脈衝的後沿保持恆定,前沿根據訊息訊號變化。此類 PWM 的波形在上圖中表示為 (b)。
脈衝的中心保持恆定,前沿和後沿根據訊息訊號變化。此類 PWM 的波形在上圖中表示為 (c)。
脈衝位置調製
**脈衝位置調製 (PPM)** 是一種模擬調製方案,其中脈衝的幅度和寬度保持恆定,而每個脈衝相對於參考脈衝的位置根據訊息訊號的瞬時取樣值變化。
傳送器必須傳送同步脈衝(或簡稱為同步脈衝)以使傳送器和接收器保持同步。這些同步脈衝有助於保持脈衝的位置。下圖解釋了脈衝位置調製。

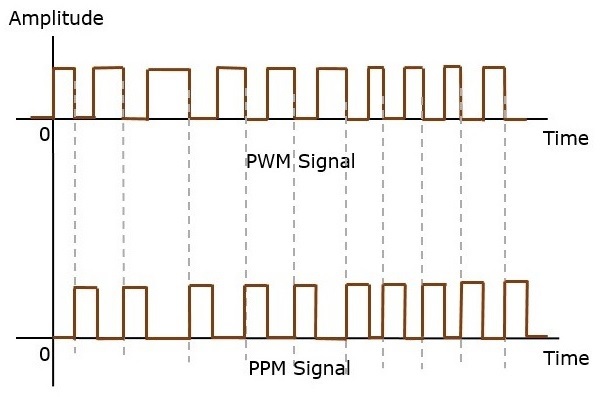
脈衝位置調製是根據脈衝寬度調製訊號完成的。脈衝寬度調製訊號的每個後沿都成為 PPM 訊號中脈衝的起始點。因此,這些脈衝的位置與 PWM 脈衝的寬度成正比。
優點
由於幅度和寬度恆定,因此處理的功率也恆定。
缺點
傳送器和接收器之間必須同步。
PAM、PWM 和 PPM 的比較
下表列出了三種調製技術的比較。
| PAM | PWM | PPM |
|---|---|---|
| 幅度變化 | 寬度變化 | 位置變化 |
| 頻寬取決於脈衝的寬度 | 頻寬取決於脈衝的上升時間 | 頻寬取決於脈衝的上升時間 |
| 瞬時發射功率隨脈衝的幅度變化 | 瞬時發射功率隨脈衝的幅度和寬度變化 | 瞬時發射功率隨脈衝的寬度保持恆定 |
| 系統複雜度高 | 系統複雜度低 | 系統複雜度低 |
| 噪聲干擾高 | 噪聲干擾低 | 噪聲干擾低 |
| 類似於幅度調製 | 類似於頻率調製 | 類似於相位調製 |
模擬通訊 - 感測器
**感測器**是一種將能量從一種形式轉換為另一種形式的裝置。在本章中,讓我們討論一下通訊系統中使用的感測器。
為什麼我們需要感測器?
在現實世界中,任何兩個附近的人之間的通訊都是藉助聲波進行的。但是,如果兩個人相距很遠,那麼在不損失任何資訊的情況下,使用聲波的物理形式來傳遞資訊就變得很困難了。
為了克服這個困難,我們可以在傳送器部分使用調製器,在接收器部分使用解調器。這些調製器和解調器使用電訊號工作。這就是為什麼我們需要一個裝置來將聲波轉換為電訊號或反之亦然。該裝置稱為感測器。
下面是感測器的簡單框圖。
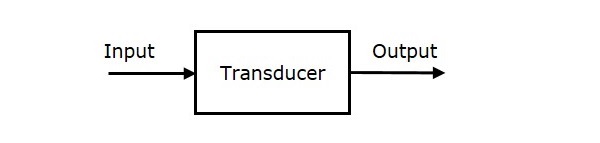
該感測器具有單個輸入和單個輸出。它將輸入端存在的能量轉換為具有另一種能量的等效輸出。基本上,感測器將非電能形式轉換為電能形式或反之亦然。
感測器的型別
根據感測器在通訊系統中的位置,我們可以將感測器分為以下**兩種型別**。
- 輸入感測器
- 輸出感測器
輸入感測器
通訊系統輸入端存在的感測器稱為**輸入感測器**。下面是輸入感測器的框圖。
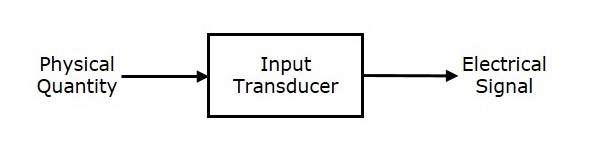
該輸入感測器將非電物理量轉換為電訊號。例如,可以使用此感測器將聲音或光等物理量轉換為電壓或電流等電量。**示例:**麥克風。
麥克風用作輸入感測器,位於資訊源和傳送器部分之間。資訊源以聲波的形式產生資訊。**麥克風**藉助振膜將這些聲波轉換為電訊號。這些電訊號可用於進一步處理。
輸出感測器
通訊系統輸出端存在的感測器稱為輸出感測器。下面是**輸出感測器**的框圖。
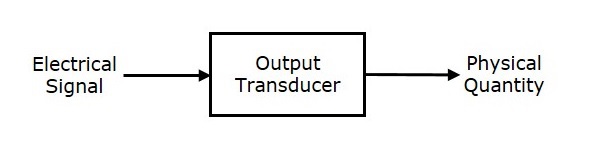
該輸出感測器將電訊號轉換為非電物理量。可以使用此感測器將電壓或電流等電量轉換為聲音或光等物理量。**示例:**揚聲器。
揚聲器用作輸出感測器,位於接收器部分和目的地之間。接收器部分的解調器產生解調輸出。因此,**揚聲器**將電訊號(解調輸出)轉換為聲波。因此,揚聲器的功能與麥克風的功能正好相反。
除了上述感測器外,通訊系統中還使用另一種感測器。此感測器可以放置在傳送器部分的末端或接收器部分的開頭。**示例:**天線。
天線是一種感測器,可以將電訊號轉換為電磁波,反之亦然。天線可以用作**發射天線**或**接收天線**。
發射天線將電訊號轉換為電磁波並輻射出去。而接收天線將接收到的波束中的電磁波轉換為電訊號。
在這種雙向通訊中,同一根天線可以用於發射和接收。