
模擬通訊 - 角調製
連續波調製中的另一種調製型別是角調製。角調製是指載波訊號的頻率或相位根據訊息訊號而變化的過程。
角調製波的標準方程為
$$s\left ( t \right )=A_c \cos \theta _i\left ( t \right )$$
其中,
$A_c$ 是調製波的幅度,與載波訊號的幅度相同
$\theta _i\left ( t \right )$ 是調製波的相位
角調製進一步分為調頻和調相。
調頻是指載波訊號的頻率隨訊息訊號線性變化的過程。
調相是指載波訊號的相位隨訊息訊號線性變化的過程。
現在,讓我們詳細討論一下。
調頻
在調幅中,載波訊號的幅度發生變化。而在調頻 (FM) 中,載波訊號的頻率根據調製訊號的瞬時幅度而變化。
因此,在調頻中,載波訊號的幅度和相位保持不變。透過觀察下圖可以更好地理解這一點。
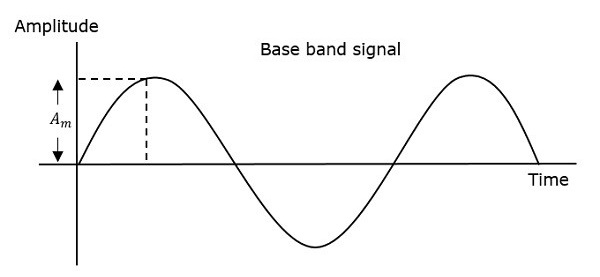

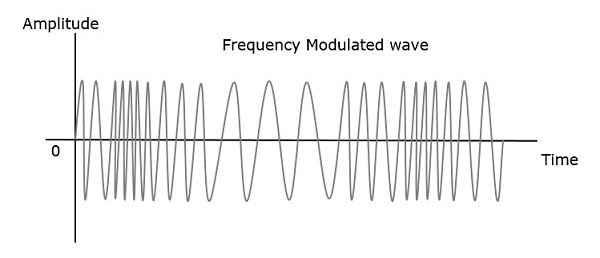
當調製訊號或訊息訊號的幅度增加時,調製波的頻率增加。類似地,當調製訊號的幅度減小時,調製波的頻率減小。請注意,當調製訊號的幅度為零時,調製波的頻率保持不變,等於載波訊號的頻率。
數學表示
FM 調製中瞬時頻率 $f_i$ 的方程為
$$f_i=f_c+k_fm\left ( t \right )$$
其中,
$f_c$ 是載波頻率
$k_t$ 是頻率靈敏度
$m\left ( t \right )$ 是訊息訊號
我們知道角頻率 $\omega_i$ 和相位 $\theta _i\left ( t \right )$ 之間的關係為
$$\omega_i=\frac{d\theta _i\left ( t \right )}{dt}$$
$\Rightarrow 2 \pi f_i=\frac{d\theta _i\left ( t \right )}{dt}$
$\Rightarrow \theta _i\left ( t \right )= 2\pi\int f_i dt$
將 $f_i$ 值代入上述方程。
$$\theta _i\left ( t \right )=2 \pi\int \left ( f_c+k_f m\left ( t \right ) \right )dt$$
$\Rightarrow \theta _i\left ( t \right )=2 \pi f_ct+2 \pi k_f\int m\left ( t \right )dt$
將 $\theta _i\left ( t \right )$ 值代入角調製波的標準方程。
$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct + 2 \pi k_f \int m\left ( t \right )dt \right )$$
這就是調頻波的方程。
如果調製訊號為 $m\left ( t \right )= A_m \cos \left ( 2 \pi f_mt \right )$, 則調頻波的方程將為
$$s\left ( t \right )=A_c \cos\left ( 2 \pi f_ct + \beta \sin \left ( 2 \pi f_mt \right ) \right )$$
其中,
$\beta$ = 調製指數 $=\frac{\Delta f}{f_m}=\frac{k_fA_m}{f_m}$
調頻波頻率(瞬時頻率)與正常載波頻率之間的差異稱為頻率偏移。用 $\Delta f$ 表示,等於 $k_f$ 和 $A_m$ 的乘積。
根據調製指數 $\beta$ 的值,FM 可以分為窄帶 FM 和寬頻 FM。
窄帶 FM
以下是窄帶 FM 的特點。
與寬頻 FM 相比,這種調頻的頻寬較小。
調製指數 $\beta$ 較小,即小於 1。
它的頻譜由載波、上邊帶和下邊帶組成。
它用於行動通訊,如警用無線電、救護車、計程車等。
寬頻 FM
以下是寬頻 FM 的特點。
這種調頻具有無限頻寬。
調製指數 $\beta$ 較大,即大於 1。
它的頻譜由載波和無限多個邊帶組成,這些邊帶位於其周圍。
它用於娛樂、廣播應用,如 FM 收音機、電視等。
調相
在調頻中,載波的頻率發生變化。而在調相 (PM) 中,載波訊號的相位根據調製訊號的瞬時幅度而變化。
因此,在調相中,載波訊號的幅度和頻率保持不變。透過觀察下圖可以更好地理解這一點。
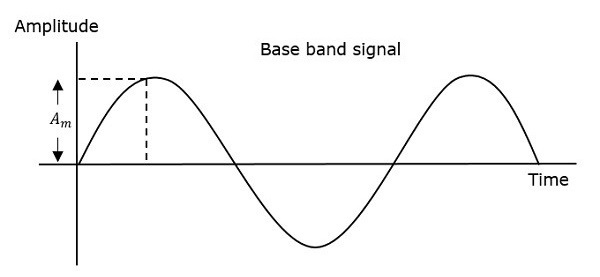
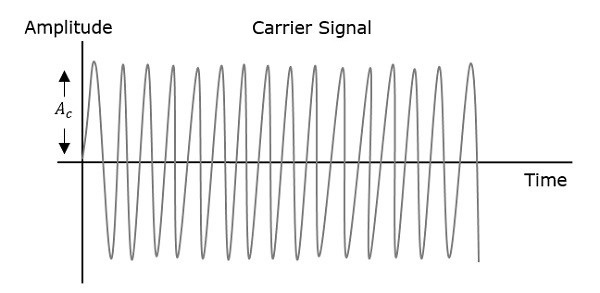

調製波的相位有無限多個點,波形可以在這些點發生相移。調製訊號的瞬時幅度改變載波訊號的相位。當幅度為正時,相位朝一個方向變化;如果幅度為負,相位則朝相反方向變化。
數學表示
調相中瞬時相位 $\phi_i$ 的方程為
$$\phi _i=k_p m\left ( t \right )$$
其中,
$k_p$ 是相位靈敏度
$m\left ( t \right )$ 是訊息訊號
角調製波的標準方程為
$$s\left ( t \right )=A_c \cos \left ( 2 \pi f_ct+\phi_i \right )$$
將 $\phi_i$ 值代入上述方程。
$$s\left ( t \right )=A_c \cos \left ( 2 \pi f_ct+k_p m \left ( t \right )\right )$$
這就是調相波的方程。
如果調製訊號為 $m\left ( t \right )=A_m \cos \left ( 2 \pi f_mt \right ) $, 則調相波的方程將為
$$s\left ( t \right )=A_c \cos\left (2 \pi f_ct+\beta \cos\left ( 2 \pi f_mt \right ) \right )$$
其中,
$\beta$ = 調製指數 = $\Delta \phi=k_pA_m$
$\Delta \phi$ 是相位偏移
調相用於移動通訊系統,而調頻主要用於 FM 廣播。