
模擬通訊 - 單邊帶抑制載波調製器
本章我們將討論產生SSB(單邊帶抑制載波)波的調製器。我們可以使用以下兩種方法產生SSB波。
- 頻率鑑別法
- 相位鑑別法
頻率鑑別法
下圖顯示了使用頻率鑑別法的SSB調製器的框圖。
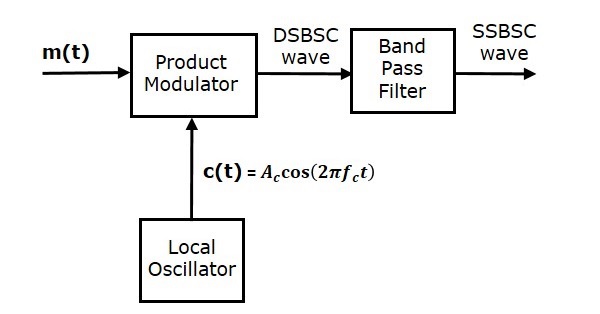
在這種方法中,我們首先使用乘法調製器產生DSB-SC(雙邊帶抑制載波)波。然後,將此DSB-SC波作為帶通濾波器的輸入。該帶通濾波器產生一個輸出,即SSB波。
選擇帶通濾波器的頻率範圍作為所需SSB波的頻譜。這意味著帶通濾波器可以調諧到上邊帶或下邊帶頻率,以獲得具有上邊帶或下邊帶的相應SSB波。
相位鑑別法
下圖顯示了使用相位鑑別法的SSB調製器的框圖。
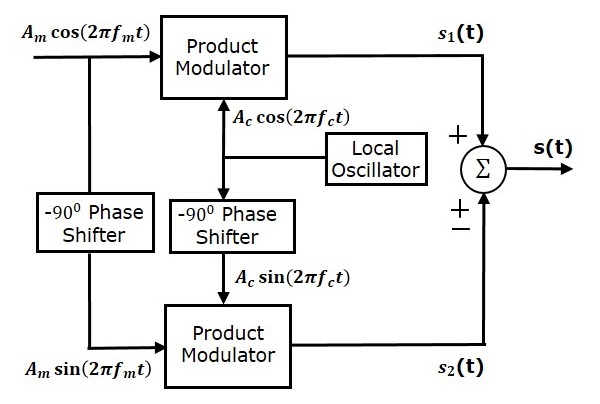
該框圖由兩個乘法調製器、兩個-90°相移器、一個本地振盪器和一個求和器組成。乘法調製器產生一個輸出,它是兩個輸入的乘積。-90°相移器產生一個輸出,該輸出相對於輸入滯後-90°。
本地振盪器用於產生載波訊號。求和器產生一個輸出,該輸出根據輸入的極性,是兩個輸入的和或差。
調製訊號$A_m \cos\left ( 2 \pi f_mt \right )$和載波訊號$A_c \cos\left ( 2 \pi f_ct \right )$直接作為輸入應用於上乘法調製器。因此,上乘法調製器產生一個輸出,它是這兩個輸入的乘積。
上乘法調製器的輸出為
$$s_1\left ( t \right )=A_mA_c \cos \left ( 2 \pi f_mt \right ) \cos\left ( 2 \pi f_ct \right )$$
$$ \Rightarrow s_1\left ( t \right )=\frac{A_mA_c}{2} \left \{ \cos \left [ 2 \pi\left ( f_c+f_m \right )t \right ]+ \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ] \right \}$$
調製訊號$A_m \cos\left ( 2 \pi f_mt \right )$和載波訊號$A_c \cos\left ( 2 \pi f_ct \right )$在作為下乘法調製器的輸入之前,先進行-90°相移。因此,下乘法調製器產生一個輸出,它是這兩個輸入的乘積。
下乘法調製器的輸出為
$$s_2\left ( t \right )=A_mA_c \cos\left ( 2 \pi f_mt-90^0 \right ) \cos\left (2 \pi f_ct-90^0 \right )$$
$\Rightarrow s_2\left ( t \right )=A_mA_c \sin \left ( 2 \pi f_mt \right )\sin \left ( 2 \pi f_ct \right )$
$\Rightarrow s_2\left ( t \right )=\frac{A_mA_c}{2} \left \{ \cos \left [ 2 \pi\left ( f_c-f_m \right )t \right ]- \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \right \}$
將$s_1\left ( t \right )$和$s_2\left ( t \right )$相加,即可得到具有下邊帶的SSB調製波$s\left ( t \right )$。
$s\left ( t \right )=\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ]+\cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ] \right \}+$
$\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ]-\cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \right \}$
$\Rightarrow s\left ( t \right )=A_mA_c \cos \left [ 2 \pi\left ( f_c-f_m \right )t \right ]$
從$s_1\left ( t \right )$中減去$s_2\left ( t \right )$,即可得到具有上邊帶的SSB調製波$s\left ( t \right )$。
$s\left ( t \right )=\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ]+\cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ] \right \}-$
$\frac{A_mA_c}{2}\left \{ \cos\left [ 2 \pi\left ( f_c-f_m \right )t \right ]-\cos\left [ 2 \pi\left ( f_c+f_m \right )t \right ] \right \}$
$\Rightarrow s\left ( t \right )=A_mA_c \cos \left [ 2 \pi\left ( f_c+f_m \right )t \right ]$
因此,透過正確選擇求和器輸入的極性,我們將得到具有上邊帶或下邊帶的SSB波。