Python中的隨機遊走實現

---

---

隨機遊走是一個每一步都隨機確定的過程，通常用於模擬不可預測的運動。它用於描述由一系列隨機移動組成的路徑。

簡單的隨機遊走可以是一維的，其中粒子必須向左或向右移動，沒有任何偏向。關於隨機遊走應用於更高維度（如二維、三維和四維）的概念，運動是在特定維度中隨機方向進行的。

每個額外的維度都會增加遊走的難度，並提供更多關於隨機過程和空間搜尋的資訊。這些理論包含了Python程式碼，用於一維、二維、三維和四維隨機遊走，以解釋如何用計算機圖形模擬它們。

所需庫的安裝

1. NumPy

用於Python數值計算的NumPy庫，用於處理陣列和執行數學運算。

語法

pip install numpy

2. Matplotlib

Matplotlib是一個繪相簿，用於在Python中建立靜態、動畫和互動式視覺化。

語法

pip install matplotlib

一維隨機遊走的實現

以下程式碼用於在Python中實現一維隨機遊走：

import numpy as np
import matplotlib.pyplot as plt

def random_walk_1d(steps):
   """Generate a 1D random walk."""
   walk = np.zeros(steps)
   for i in range(1, steps):
      step = np.random.choice([-1, 1])
      walk[i] = walk[i - 1] + step
   return walk

# Number of steps
steps = 1000
walk = random_walk_1d(steps)

# Plot the random walk
plt.figure(figsize=(10, 6))
plt.plot(walk, label='1D Random Walk')
plt.xlabel('Steps')
plt.ylabel('Position')
plt.title('1D Random Walk')
plt.legend()
plt.show()

輸出

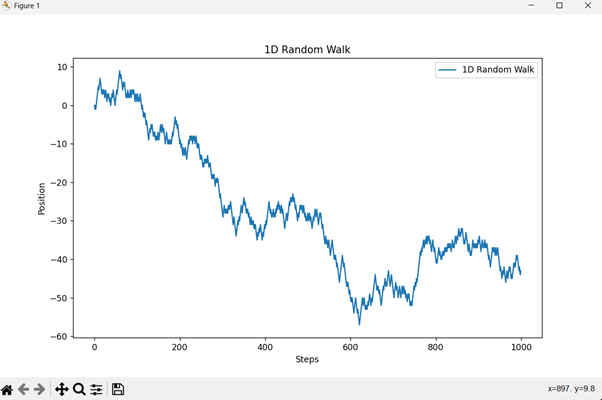
程式碼解釋

• **匯入** - numpy用於數值運算。matplotlib.pyplot用於繪製遊走。**random_walk_1d**
• **函式** - 建立一維隨機遊走。
  對於每一步，隨機決定向左移動(-1)還是向右移動(+1)。
  累加這些步數以計算每一步的位置。
• **繪圖** - 繪製位置與步數的關係圖，以便視覺化隨機遊走。

二維隨機遊走的實現

以下程式碼用於在Python中實現二維隨機遊走：

import numpy as np
import matplotlib.pyplot as plt

def random_walk_2d(steps):
   """Generate a 2D random walk."""
   positions = np.zeros((steps, 2))
   for i in range(1, steps):
      step = np.random.choice(['up', 'down', 'left', 'right'])
      if step == 'up':
         positions[i] = positions[i - 1] + [0, 1]
      elif step == 'down':
         positions[i] = positions[i - 1] + [0, -1]
      elif step == 'left':
         positions[i] = positions[i - 1] + [-1, 0]
      elif step == 'right':
         positions[i] = positions[i - 1] + [1, 0]
   return positions

# Number of steps
steps = 1000
positions = random_walk_2d(steps)

# Plot the random walk
plt.figure(figsize=(10, 10))
plt.plot(positions[:, 0], positions[:, 1], label='2D Random Walk')
plt.xlabel('X Position')
plt.ylabel('Y Position')
plt.title('2D Random Walk')
plt.legend()
plt.grid(True)
plt.show()

輸出

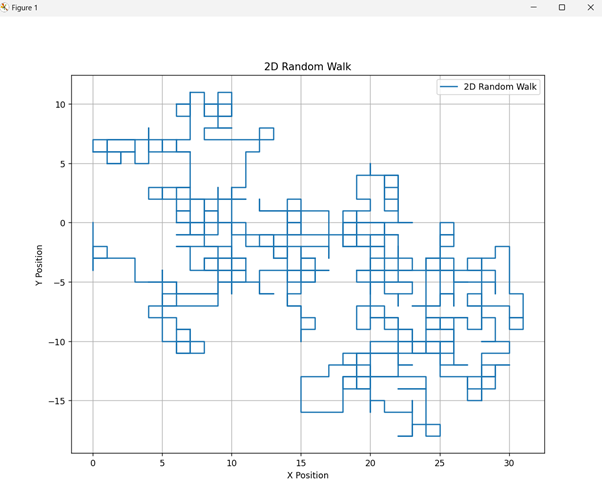
程式碼解釋

**向四個方向之一移動** - 向上、向下、向左或向右。相應地更新位置並記錄每一步。

三維隨機遊走的實現

以下程式碼用於在Python中實現三維隨機遊走：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def random_walk_3d(steps):
   """Generate a 3D random walk."""
   positions = np.zeros((steps, 3))
   for i in range(1, steps):
      step = np.random.choice(['x+', 'x-', 'y+', 'y-', 'z+', 'z-'])
      if step == 'x+':
         positions[i] = positions[i - 1] + [1, 0, 0]
      elif step == 'x-':
         positions[i] = positions[i - 1] + [-1, 0, 0]
      elif step == 'y+':
         positions[i] = positions[i - 1] + [0, 1, 0]
      elif step == 'y-':
         positions[i] = positions[i - 1] + [0, -1, 0]
      elif step == 'z+':
         positions[i] = positions[i - 1] + [0, 0, 1]
      elif step == 'z-':
         positions[i] = positions[i - 1] + [0, 0, -1]
   return positions

# Number of steps
steps = 1000
positions = random_walk_3d(steps)

# Plot the random walk
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
ax.plot(positions[:, 0], positions[:, 1], positions[:, 2], label='3D Random Walk')
ax.set_xlabel('X Position')
ax.set_ylabel('Y Position')
ax.set_zlabel('Z Position')
ax.set_title('3D Random Walk')
ax.legend()
plt.show()

輸出

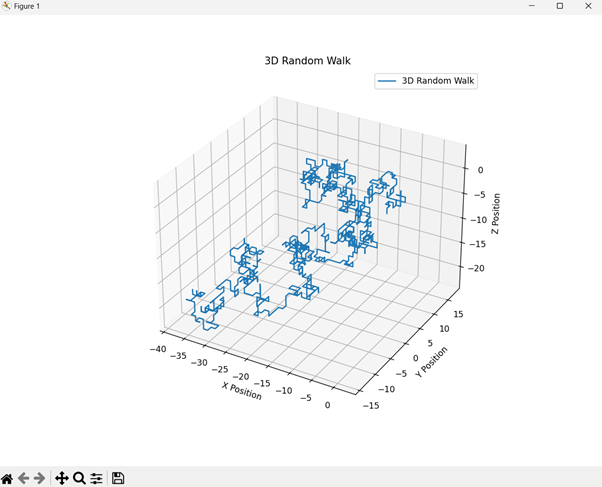
程式碼解釋

• **向六個方向之一移動** - x+、x-、y+、y-、z+或z-。更新三維空間中的位置。
• **繪圖** - 使用matplotlib繪製二維隨機遊走。使用mpl_toolkits.mplot3d進行三維視覺化繪製三維隨機遊走。

四維隨機遊走的實現

以下程式碼用於在Python中實現四維隨機遊走：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def random_walk_4d(steps):
   """Generate a 4D random walk."""
   positions = np.zeros((steps, 4))
   for i in range(1, steps):
      direction = np.random.choice(['x+', 'x-', 'y+', 'y-', 'z+', 'z-', 'w+', 'w-'])
      if direction == 'x+':
         positions[i] = positions[i - 1] + [1, 0, 0, 0]
      elif direction == 'x-':
         positions[i] = positions[i - 1] + [-1, 0, 0, 0]
      elif direction == 'y+':
         positions[i] = positions[i - 1] + [0, 1, 0, 0]
      elif direction == 'y-':
         positions[i] = positions[i - 1] + [0, -1, 0, 0]
      elif direction == 'z+':
         positions[i] = positions[i - 1] + [0, 0, 1, 0]
      elif direction == 'z-':
         positions[i] = positions[i - 1] + [0, 0, -1, 0]
      elif direction == 'w+':
         positions[i] = positions[i - 1] + [0, 0, 0, 1]
      elif direction == 'w-':
         positions[i] = positions[i - 1] + [0, 0, 0, -1]
   return positions

# Number of steps
steps = 1000
positions = random_walk_4d(steps)

# Plot a 4D random walk by projecting onto 3D
fig = plt.figure(figsize=(10, 10))

# 3D projection using first three dimensions
ax1 = fig.add_subplot(121, projection='3d')
ax1.plot(positions[:, 0], positions[:, 1], positions[:, 2], label='Projection: X-Y-Z')
ax1.set_xlabel('X Position')
ax1.set_ylabel('Y Position')
ax1.set_zlabel('Z Position')
ax1.set_title('4D Random Walk (Projection)')
ax1.legend()

# Another 3D projection using last three dimensions
ax2 = fig.add_subplot(122, projection='3d')
ax2.plot(positions[:, 1], positions[:, 2], positions[:, 3], label='Projection: Y-Z-W')
ax2.set_xlabel('Y Position')
ax2.set_ylabel('Z Position')
ax2.set_zlabel('W Position')
ax2.set_title('4D Random Walk (Projection)')
ax2.legend()

plt.show()

輸出

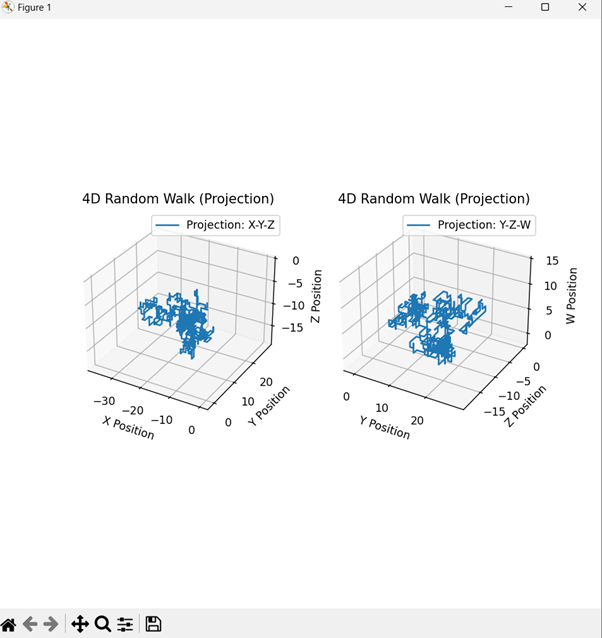
程式碼解釋

• **random_walk_4d函式** - 向八個方向之一移動：x+、x-、y+、y-、z+、z-、w+、w-。更新四維空間中的位置。
• **繪圖** - 由於四維資料太複雜而無法直接視覺化，我們將其對映到三維空間，以便我們可以很好地視覺化。第一個子圖投影到X-Y-Z空間。第二個子圖投影到Y-Z-W空間。
• **視覺化** - 在這些三維投影中，遊走的演變是清晰的——你可以從這裡瞭解四維遊走的行為。