
第8章 - 小數
小數的介紹
“小數”一詞來源於拉丁語“decimus”,意思是“十分之一”。
小數是用一個小點將數字的兩個數字隔開來寫的。這個點被稱為小數點。例如,23.45、3.14、0.02等。
整數和分數的組合
小數類似於分數,它們也表示整體的一部分。例如,3½是一個帶分數,可以寫成小數3.5。
- 小數點左邊的數字表示整數,而
- 小數點右邊的數字表示分數部分。
小數用於表示介於兩個連續整數之間的數字。

在小數中,小數點左邊的數字像整數一樣讀,而小數點右邊的數字則逐個讀。例如,47.28讀作“四十七點二八”。
分數到小數
分數和小數密切相關。透過進行分數中的除法,可以將分數轉換為小數。例如,
${7}/{4}$ = 1.75
小數表示一個大於整數但小於其連續下一個整數的數字,類似於帶分數。
小數的位值
整數的位值
我們知道,整數的不同數字根據其在位值表中的位置具有不同的位值。
例如,在整數27中,數字2在十位,數字7在個位。
- 向左移動時,位值以10為倍數增加。
- 向右移動時,位值以${1}/{10}$為倍數減少。
小數的位值
在寫小數時,小數點用於將小數部分與整數部分隔開。
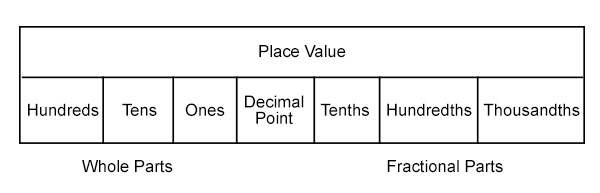
與整數一樣,小數也有自己明確定義的位值系統。
- 當我們將一個整體分成十等份時,就形成了十分位。
- 當我們將十分之一再分成十等份時,就形成了百分位。
整數部分和小數部分
- 小數點左側的所有位值稱為整數部分。
- 小數點右側的所有位值稱為小數部分。
示例:繪製小數218.95的位值表。
解決方案:
$$218.95 = 200 + 10 + 8 + {9}/{10} + {5}/{100}$$
位值表

比較小數
讓我們用例子來學習如何比較兩個小數。
示例:比較小數12.9和15.4。
解決方案:
- 首先,比較小數的整數部分。
- 這裡,它們是12和15。
- 顯然,12 < 15。
因此,12.9 < 15.4
如果兩個小數的整數部分相等,則比較它們的小數部分。
示例:比較小數50.54和50.45。
解決方案:
- 整數部分相同,即50。
- 因此,讓我們比較小數部分。
- 顯然,54 > 45。
因此,50.54 > 50.45
使用位值圖表
位值圖表可用於比較小數。
這是一個兩步過程
- 將數字寫入其位值圖表中。
- 然後,從最左邊的位置到最右邊的位置比較數字。
示例:比較小數4.5和4.56。
解決方案:
將數字寫入其位值圖表中,

用0作為佔位符填充空位值。

比較每個位置上的數字,
4.5 < 4.56
4.5小於4.56。
數軸上小數的表示
要在數軸上表示一個小數,首先將其轉換為對應分數,然後在數軸上表示。
要在數軸上標記任何小數,
- 首先,找到該數字所在的兩個連續整數。
- 然後,將這兩個整數之間的間隔分成十等份(或十分之一)。
小數點後有多於2位數字的小數很難在數軸上表示。
例如,要在數軸上表示0.75,必須將0和1之間的間隔分成100等份,而使用筆和紙來完成這項任務並不容易。
示例:在數軸上表示小數5.7。
解決方案:
將5.7分成整數和小數,
5.7 = 5 + 0.7
所以,5.7位於5和6之間。
接下來,將5和6之間的區域分成10等份。
在數軸上,當兩個整數之間的間隔分成10等份時,每一份表示一個整體的十分之一。

因此,5和6之間第7條線表示5.7。

示例:在數軸上表示小數0.5。
解決方案:
將小數轉換為分數,
0.5 = ${5}/{10}$
分子 > 分母,所以它是一個真分數,位於0和1之間。
將0和1之間的區域分成10等份。

從0向右的第5條線在數軸上是${5}/{10}$或0.5。
將分數轉換為小數
將小數轉換為分數
要將一個小數轉換為分數,
- 首先,將數字寫成不帶小數點的形式。
- 將此數字視為分數的分子。
- 分數的分母將是1,後面跟與數字中小數點後數字個數相同的零。
例如,
$$0.43 = {43}/{100} \: 和 \: 0.8 = {8}/{10}$$
同樣地,
$$9.12 = {912}/{100} = 9{12}/{100}$$
示例:將小數34.36轉換為分數。
解決方案:
重寫34.36,
= 34 + 0.36
= 34 + ${36}/{100}$
= 34 ${36}/{100}$
= ${3436}/{100}$
還有另一種將小數轉換為分數的方法。
根據位值,
34.36 = 3 × 10 + 4 × 1 + ${3}/{10}$ + ${6}/{100}$
= 30 + 4 + ${3}/{10}$ + ${6}/{100}$
= ${3436}/{100}$ = 34${36}/{100}$
將分數轉換為小數
要將分數轉換為其等效小數,進行長除法,直到餘數為0。例如,
${3}/{2}$ = 1.5
同樣地,
${3}/{4}$ = 0.75
如果分數的分母是10的冪(如100或1000),則將分數轉換為其等效小數非常容易。
取分子並在右側放置一個小數點,小數點後的位數與分母中0的個數相同。
例如,
${34}/{100}$ = 0.34 ; ${6}/{10}$ = 0.6 ; ${764}/{1000}$ = 0.764
如果分數的分母不是10的冪,則找到其分母為10的冪的等效分數。
例如,
${13}/{25}$ = ${13 × 4 }/{25 × 4}$ = ${52}/{100}$ = 0.52
小數的實際應用
我們經常需要處理非整數的數字。在這種情況下,小數是不可避免的。例如,我們購買物品的價格以小數表示,如髮油的價格可能是86.75盧比
小數用於金融、測量長度、查詢物體的重量以及更多其他地方。
金融中的小數
在金融中,小數用於以不同的面額來寫一個值。
示例:
1盧比有100派士。所以,
1派士= ${1}/{100}$盧比
39派士= ${39}/{100}$盧比= 0.39盧比
同樣地,
293派士= 200派士+ 93派士
= 2盧比和93派士= 2.93盧比
測量中的小數
小數在測量長度中起著重要作用。最常見的長度測量單位是公里(km)、米(m)、釐米(cm)和毫米(mm)。
1公里= 1000米
1米= 100釐米
1釐米= 10毫米
示例:將23釐米轉換為米。
解決方案:
100釐米= 1米
⇒ 1釐米= ${1}/{100}$米
⇒ 23釐米= ${23}/{100}$米= 0.23米
示例:將2.5米轉換為釐米。
解決方案:
2.5米= 2米+ 0.5米
= (2 × 100)釐米+ (${5}/{10}$ × 100)釐米
= 200釐米+ 50釐米
= 250釐米
示例:將45克表示為千克。
解決方案:
“千”指的是1000。
1000克= 1千克
⇒ 1克= ${1}/{1000}$千克
⇒ 45克= ${45}/{1000}$千克= 0.045千克
小數的加法
加法是最基本的算術運算,用於求兩個數的和。
列豎式加法
在寫數字時,相同位值的數字必須位於同一列。例如,

兩個小數的加法
在加兩個小數時,
- 將數字一個放在另一個的下面。
- 對齊它們的小數點。
- 然後,從右到左逐位相加。
示例:加小數5.47和2.16。
解決方案:
首先,根據它們的位值將數字放在相應的列中,並對齊小數點

從最右邊的位值開始加法。
7 + 6 = 13
所以,我們寫下3並將1進位到十分位。

接下來,加上十分位,
4 + 1 = 5
加上來自上一步加法的進位,我們得到
5 + 1 = 6

最後,加上個位,
5 + 2 = 7

因此,5.47 + 2.16 = 7.63
如果一個小數的位數少於另一個數,則在整數部分之前和小數部分之後新增0作為佔位符。它不會改變小數的值。
例如,
7.65 = 7.650 = 07.650
小數的減法
列豎式用於減去兩個小數。
步驟如下
- 將數字一個放在另一個的下面,使它們的小數點對齊。
- 從最右邊的列開始,一直減到所有列都減完。
- 如果無法減法,則從下一較高位值借位並減去。
示例:減去5.47 − 2.16
解決方案
將小數寫在數位表中,並使小數點對齊。
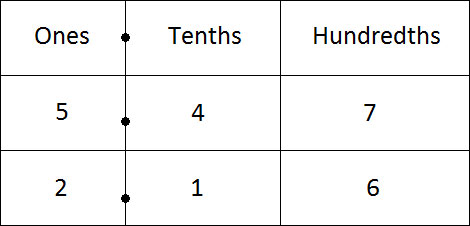
從最右邊的數位開始減。
7 − 6 = 1
所以,我們在百分位上寫 1。
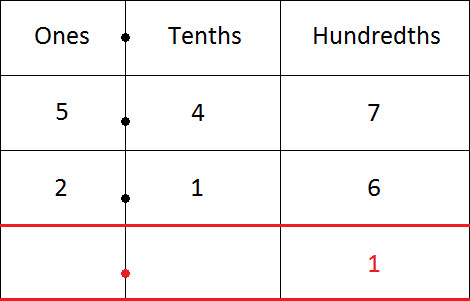
接下來,減去十分位上的數字。
4 − 1 = 3
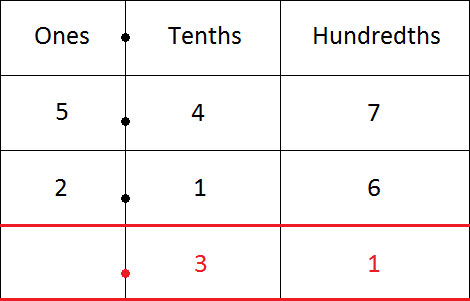
將小數點向下移。
最後,減去個位上的數字。
5 − 2 = 3
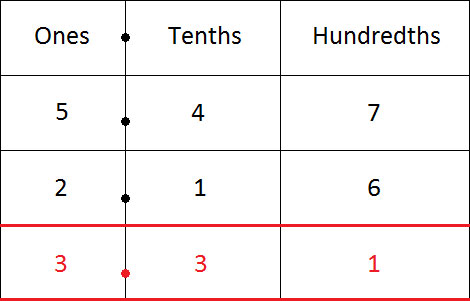
結果 5.47 − 2.16 = 3.31
示例:傑克在一家雜貨店購買了一支牙膏,價格為 30.25 印度盧比。他給了店主 50 印度盧比。他應該找回多少錢?
解決方案:
將數字按列寫出,使小數點對齊。
- 從最右邊的列開始。
- 0 > 5,所以從十分位借 10。
- 從 10(借位後)中減去 5,得到同一列中的 5。
- 在下一列中,從 9 中減去 2 得到 7。
- 接下來,將小數點向下移。
- 在下一列中,從 9 中減去 0 得到 9。
- 最後,在最左邊的列中,從 4 中減去 3 得到 1。

因此,傑克應該找回 19.75 印度盧比。