
第4章 - 基本幾何概念
幾何圖形簡介
術語“幾何”來自希臘語Geometron。Geo表示地球,metron表示測量。幾何概念體現在各種藝術形式、測量、建築、工程和設計中。
從桌子和書本等基本物體到世界著名的紀念碑,一切都可以用它們的幾何形狀來定義。
著名紀念碑及其形狀
吉薩大金字塔以其獨特的形狀而聞名。金字塔的所有面都是三角形,底座是正方形。

泰姬陵有正方形底座、圓形穹頂和四個圓柱形尖塔。

比薩斜塔有圓形底座和圓柱形塔身。

不僅是著名的紀念碑,我們還可以用幾何形狀來定義即使是最簡單的物體,例如書籍、桌子和瓶子。
點、線段、射線和直線
像正方形和三角形這樣的幾何圖形由點、線、射線和角等基本單元組成。
點
拿一支削尖的鉛筆,在一張紙上畫一個點。這個點是無形的細小點。這個微小的點叫做點。
我們在幾何圖形上使用點來標記特定位置。當我們將幾個點放在一起時,我們用A、B、C、D等命名它們,以便於識別。
線段
我們將兩個點連線起來得到一條線段。線段${AB}↖{−}$連線點A和B。

直線
如果線段在A方向以外延伸,在B方向以外延伸,沒有終點,那麼我們就得到一條直線。直線表示為${AB}↖{↔}$。

相交線和平行線
當兩條直線在某一點相遇時,我們稱它們為相交線,它們的交點稱為交點。
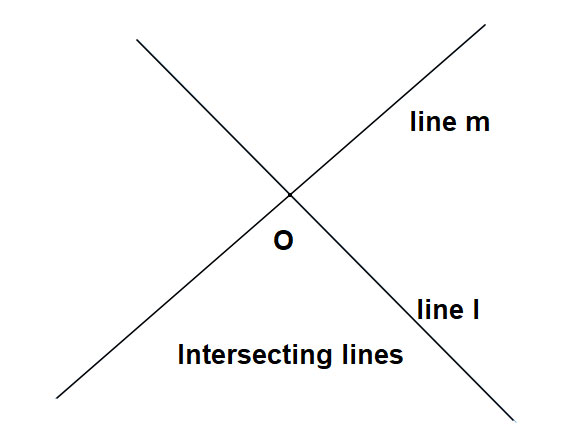
當兩條直線永不相交時,我們稱它們為平行線。
射線
射線是直線的一部分,它從直線上的一個點開始,並無限地朝某個方向延伸。
射線${AB}↖{→}$從A開始,向B方向延伸,並超出B。

在幾何上,射線有一個起點,沒有終點。當手電筒或燈泡發光時,我們會得到光線。我們也從太陽那裡得到光線。
曲線和多邊形
曲線可以定義為點在任何方向上的連續運動。因此,所有可能的形狀都可以歸類為曲線,因為所有形狀都是由點在單維或多維空間中的運動形成的。
項鍊、蛇和鬆弛的繩索是曲線圖形的一些例子。

通常,曲線是不直的實體,但在數學中,即使是直線也是曲線。
曲線的型別
- 有些曲線不會與自身相交。這些稱為簡單曲線。
- 沒有開口的曲線稱為閉合曲線。
- 不閉合路徑的曲線稱為開曲線。
多邊形
在數學上,多邊形是二維閉合圖形,完全由線段組成。構成多邊形的線段稱為多邊形的邊。

兩條邊相交的公共點稱為頂點(單數形式為頂點)。多邊形的頂點數等於其邊數。