
第五章 - 認識基本圖形
引言
線段、角、三角形、四邊形、多邊形和圓是基本圖形的例子。任何複雜的幾何圖形都可以由這些基本圖形構成。

例如,一個正四稜錐是由四個等腰三角形和一個正方形底面組成的。
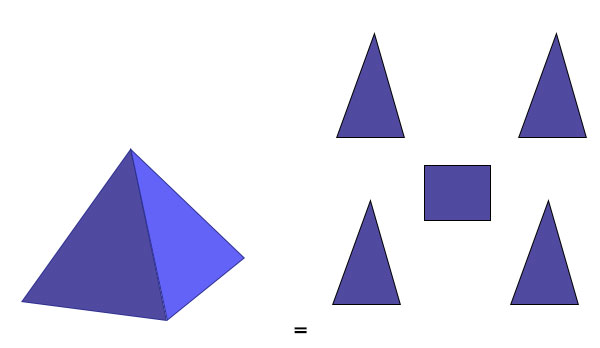
一個六稜柱是由6個矩形和兩個六邊形組成的。

即使是基本圖形也有不同的形式,例如三角形可以是等邊三角形、等腰三角形或不等邊三角形。類似地,四邊形可以是矩形、正方形或平行四邊形。

測量線段
線段的長度用毫米和釐米來測量。
觀察比較
如果我們將兩條線段並排放置,那麼只需觀察就可以很容易地比較它們的長度。

使用量角器比較
當兩條線段長度幾乎相等時,我們必須使用量角器來比較它們的長度。(原文此處應為“卡尺”或“圓規”,此處根據上下文進行調整)

使用尺子測量
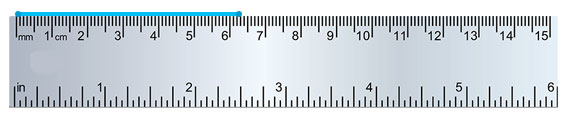
尺子標有釐米和毫米。尺子上兩個大刻度之間的差是1釐米,而兩個小刻度之間的差是1毫米。
將尺子沿著線段放置,尺子的零點與線段的一個端點對齊,測量另一個端點在尺子上的讀數,即可得到線段的長度。
使用尺子和量角器測量
首先,使用量角器,將其兩臂張開,固定線上段的兩端點上。(原文此處應為“卡尺”或“圓規”,此處根據上下文進行調整)

然後,拿起量角器,將其放在尺子上,使量角器的一臂與尺子的零點重合。(原文此處應為“卡尺”或“圓規”,此處根據上下文進行調整)從量角器的另一臂上讀取讀數。(原文此處應為“卡尺”或“圓規”,此處根據上下文進行調整)
角的型別
平行線
平行線永不相交。

相交線
當兩條線在一點相交時,它們被稱為相交線;交點被稱為交點。

兩條相交線形成四個角;通常是兩個銳角和兩個鈍角。
垂直線
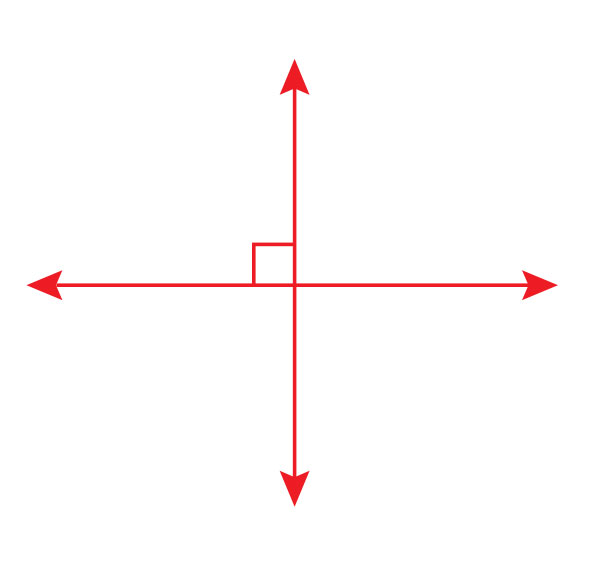
構成“+”號的兩條線稱為垂直線。垂直線形成的角稱為直角。
角
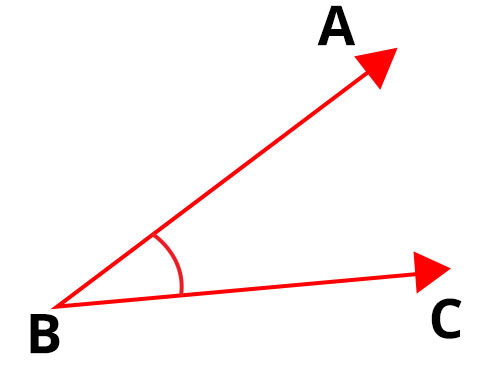
當兩條線段在一點相交時,它們形成一個角。線段稱為角的邊。ABC是一個角。
直角
呈“L”形的角稱為直角,角的兩邊互相垂直,或成90°。

銳角
小於直角(90度)的角稱為銳角。
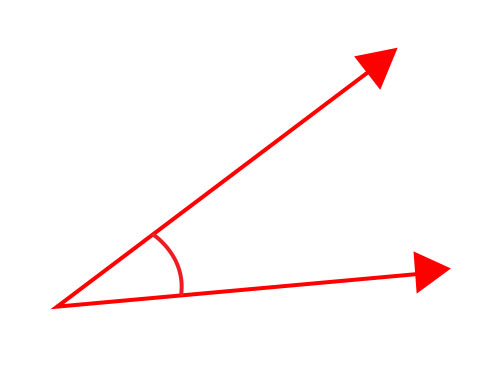
鈍角
大於直角(90度)但小於平角的角稱為鈍角。
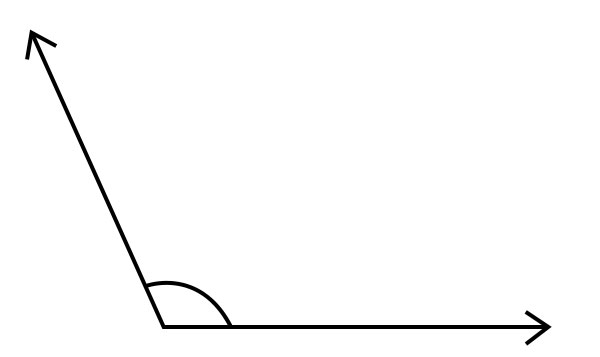
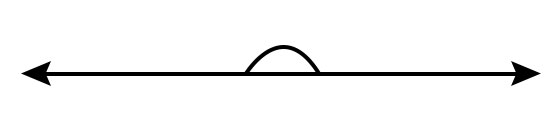
平角
當形成角的射線指向完全相反的方向時,就會形成平角。平角等於180°。
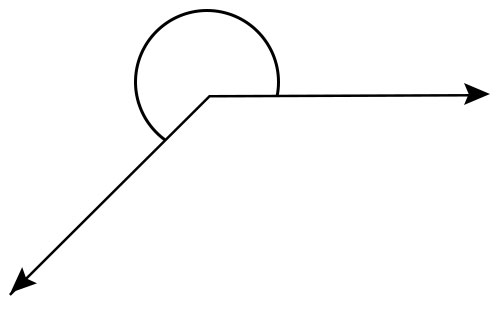
優角
介於180°和360°之間的角稱為優角。
周角
當角的一條邊繞著另一條邊(底邊)旋轉一週時,就會形成周角。周角等於360°。
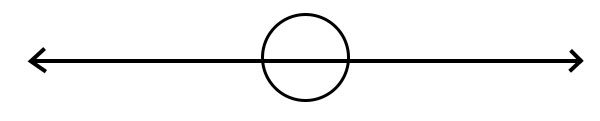
測量角
角是用一種叫做量角器的工具來測量的,這種工具可以在文具盒裡找到。
就像尺子一樣,量角器也有刻度,但形狀是半圓形。角的單位是度。刻度從0°開始,到180°結束。
測量銳角
將量角器放置在角的頂點處,使其中心與頂點重合。
確保量角器的0°線或基線與銳角的底邊重合。

從角的另一條邊在量角器上的位置記錄測量值。
測量直角
當角的另一條邊指向量角器上的90°時,它被稱為直角。

測量鈍角
當角的另一條邊指向量角器上90°到180°之間的任何位置時,它就是一個鈍角。

測量優角
優角的度數介於180°和360°之間。我們不能直接用量角器測量優角,因為它最大隻能測量180°。因此,優角是間接測量的。
銳角/鈍角的一對邊在相對側也形成一個優角。在這種情況下,銳角/鈍角的度數 = 360° - 優角的度數。

測量平角和周角
平角的度數為180°。使用量角器,可以測量平角,顯示180°的讀數。周角的度數為360°,是平角度數的兩倍。

垂直平分線
平分線是一條將另一條線段分成兩等份的線。如果一條線與另一條線成90°角,則稱這條線垂直於另一條線。然後稱這兩條線為垂直線。
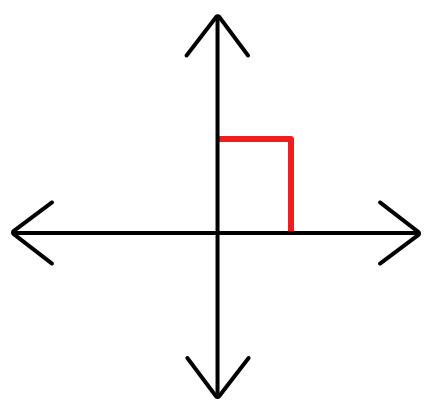
線段的垂直平分線必須垂直於它,並且也將其分成兩等份。
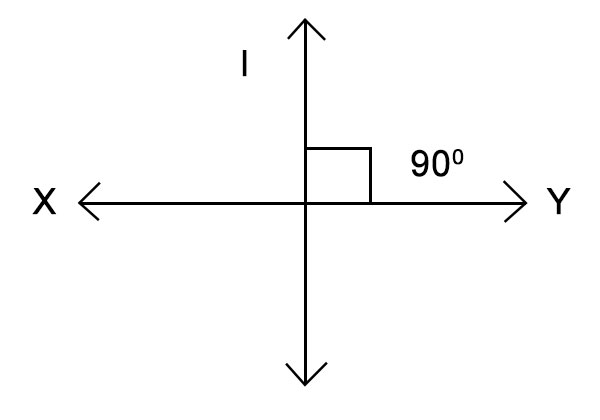
在下面的例子中,平分線不垂直於XY,所以它不是垂直平分線。

三角形的型別
三角形是一種基本圖形,它是邊數最少的幾何圖形。三角形有三條邊和三個角。
我們可以根據三角形的邊和角的特性對其進行分類。
銳角三角形
如果三角形的所有角都小於90°,則該三角形是銳角三角形或銳角三角形。

直角三角形
如果三角形的兩個角是銳角,第三個角是直角或90°,則這樣的三角形稱為直角三角形。

鈍角三角形
如果三角形的兩個角是銳角,第三個角是鈍角或大於90°的角,則這樣的三角形稱為鈍角三角形或鈍角三角形。
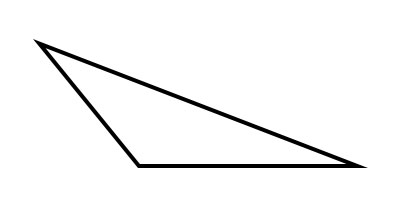
等邊三角形
在一個三角形中,如果三條邊的長度相等,則該三角形稱為等邊三角形。在等邊三角形中,所有角都等於60°。

等腰三角形
在一個三角形中,如果發現兩條邊的長度相等,則該三角形稱為等腰三角形。在等腰三角形中,與相等邊相對的角也相等。
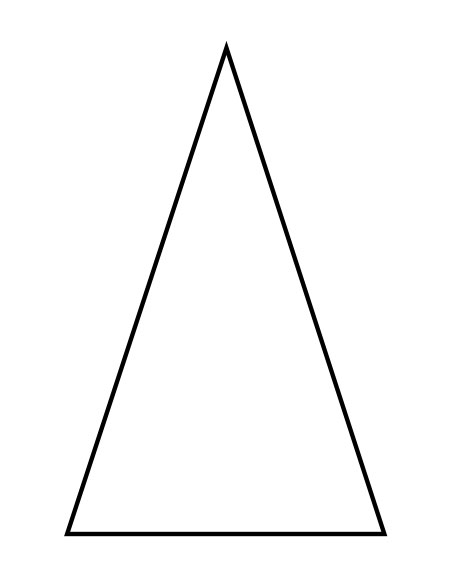
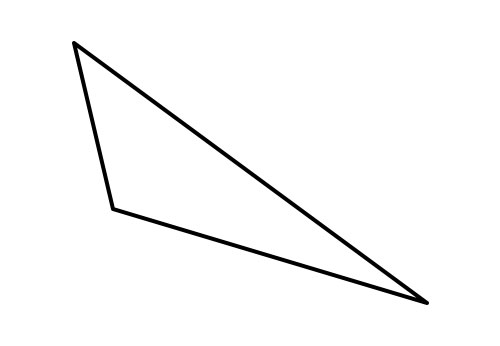
不等邊三角形
在一個三角形中,如果邊的長度不同或不相等,則該三角形稱為不等邊三角形。它的三個角也不相等。
四邊形的型別
四邊形是一種有四條邊和四個角的多邊形。四邊形有很多型別,例如矩形、正方形、平行四邊形、菱形和梯形。
矩形
矩形是一種四邊形。它有兩對邊長度相等且互相平行。所有角都等於90°。

矩形的對角線長度相等,並且互相平分。
正方形
正方形的所有邊都相等且互相平行。所有角都等於90°。

正方形是矩形的一種特殊情況,其中長和寬相等。對角線互相垂直平分。
平行四邊形
這是一種四邊形,其中對邊相等且互相平行。對角相等,鄰角不相等。
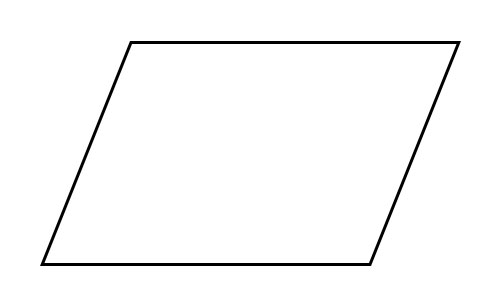
所有矩形和正方形都是平行四邊形。但並非所有平行四邊形都是矩形或正方形。
菱形
菱形是一種特殊的四邊形,它的所有邊都相等。
- 對邊相等且互相平行。
- 對角相等,但鄰角不相等。
- 對角線不相等,但互相垂直平分。

- 所有菱形都是平行四邊形,但並非所有平行四邊形都是菱形。
- 所有正方形都是菱形,但並非所有菱形都是正方形。
梯形
梯形是一種四邊形,其中有一對對邊平行。

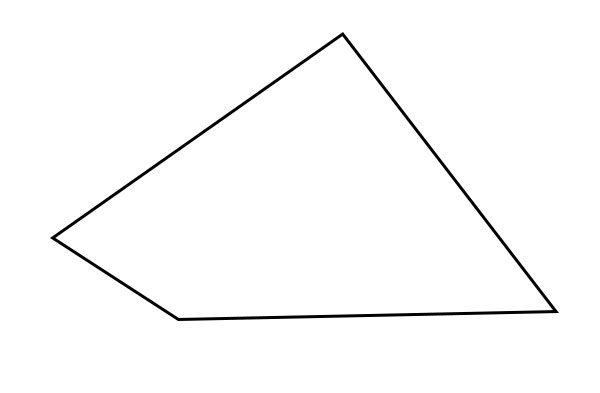
四邊形
任何四邊形都稱為四邊形。矩形、正方形、梯形、平行四邊形和菱形都是四邊形的特殊型別。沒有邊或角相等的四邊形是普通四邊形。
四邊形的對角線
- 矩形和正方形的對角線相等。
- 平行四邊形和菱形的對角線不相等。
- 正方形和菱形的對角線互相垂直。
- 矩形、正方形、平行四邊形和菱形的對角線互相平分。
多邊形的型別
多邊形是由線段組成的封閉圖形。多邊形的名稱取決於它們有多少條邊。
- 三角形是邊數最少的多邊形,即三條邊。
- 四邊形是有四條邊的多邊形。
- 五邊形是一個五邊多邊形。
- 六邊形是一個六邊多邊形。
- 八邊形是一個八邊多邊形。
正多邊形
邊長相等且角相等的多邊形稱為正多邊形。
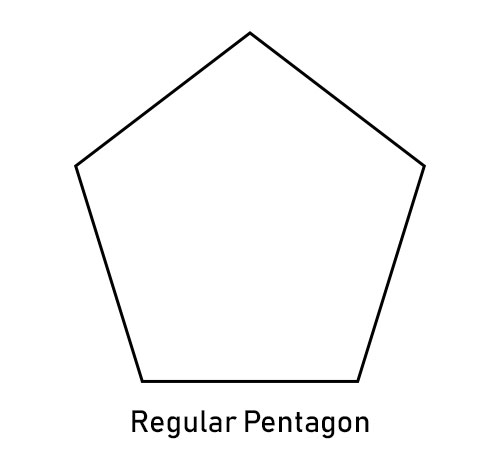
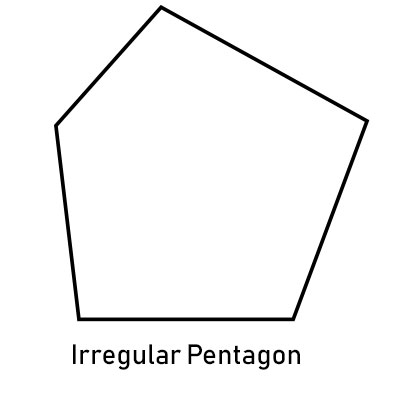
不正多邊形
邊長和角不相等的多邊形稱為不正多邊形。
隨著多邊形邊數的增加,其形狀越來越接近圓形。因此,圓可以看作是一個具有無限多條邊的多邊形。
多邊形的對角線
對角線是連線多邊形中任意兩條不相鄰頂點的線段。
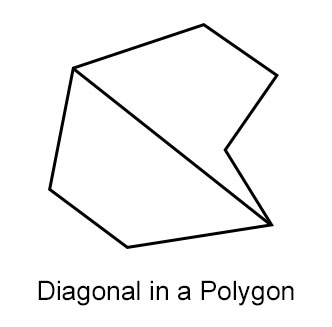
N邊形對角線的數量由公式 ${N (N − 3)}/{2}$ 給出。
五邊形的對角線條數 = ${5(5 − 3)}/{2}$ = 5
六邊形的對角線條數 = ${6(6 − 3)}/{2}$ = 9


三維形狀
維度
- 點是一個具有固定位置的微小點。它沒有維度。
- 線是一維點集,具有長度。
- 平面是線的集合。它具有兩個維度:**長度**和**寬度**。
- 長方體是線的集合,具有三個維度:**長度**、**寬度**和**高度**。
一些基本的二維基本形狀

我們可以用這些二維基本形狀構建三維形狀。
長方體
三維長方體是由許多矩形組合而成的。
- 它有6個面或平面。
- 這些面在稱為**稜**的線上相交。長方體有12條稜。
- 三條或更多條稜在稱為**頂點**的點上相交。長方體有8個頂點。

正方體
正方體是由許多正方形組合而成的。它也像長方體一樣有6個面、12條稜和8個頂點。
- 在正方體中,所有稜都相等。在長方體中,稜的長度不相等。
- 所有正方體都是長方體,但並非所有長方體都是正方體。

三角稜柱
三角稜柱是一個三維形狀,它有5個面,即兩個三角形底面和3個矩形側面。它有9條稜和6個頂點。

稜柱可以由矩形底面、正方形底面、五邊形底面和六邊形底面構成。

矩形稜柱只有長方體,正方形稜柱只有正方體。
正方形錐體
它是由正方形和三角形構成的三維形狀。它有一個正方形底面和4個三角形側面。它有5個面、8條稜和5個頂點。

三角錐體或四面體
它是由四個三角形構成的三維形狀。它有4個三角形面、6條稜和4個頂點。

圓柱體、圓錐體和球體
圓柱體、圓錐體和球體是沒有直邊的三維形狀。
- 圓柱體由兩個圓和一個矩形構成。它有兩個圓形底面。
- 圓錐體由一個圓形底面和一個扇形構成。
- 球體沒有底面、面、稜和頂點。球體是二維圓的三維版本。
