
第13章 - 對稱
對稱的介紹
對稱廣泛應用於幾何學和建築學的研究。從數學角度來說,對稱意味著一個形狀在某種移動方式下(旋轉、翻轉或滑動)可以完全與另一個形狀重合。
對稱物體
當一個影像或物體被分成兩個相等的半部分,其中一半是另一半的複製品時,我們可以說該影像或物體是對稱的。例如:

非對稱物體
不顯示對稱性的物體稱為非對稱物體。例如:

對稱軸
將二維物體分成映象兩半的直線稱為該物體的對稱軸。一個物體可以有多條對稱軸。例如:
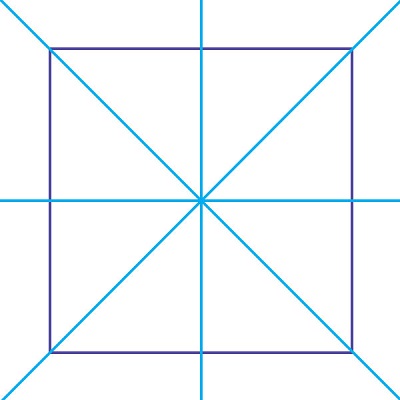
對稱軸
將二維物體分成映象兩半的直線稱為對稱軸。對稱軸不依賴於方向。它可以是垂直的、水平的或傾斜的。
對稱物體可以有多條對稱軸。非對稱物體沒有對稱軸。
1條對稱軸
如果只有一個直線可以將物體分成兩半,則該物體具有1條對稱軸。

2條對稱軸
如果有兩條直線可以將物體分成兩半,則該物體具有2條對稱軸。
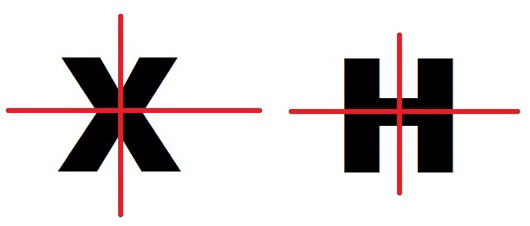
3條對稱軸
如果有三條直線可以將物體分成兩半,則該物體具有3條對稱軸。
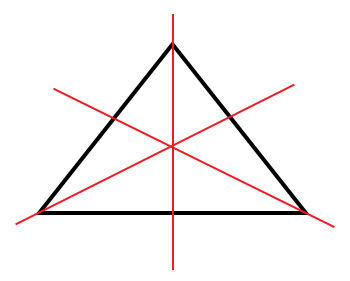
無限條對稱軸
如果有無限條直線可以將物體分成兩半,則該物體具有無限條對稱軸。
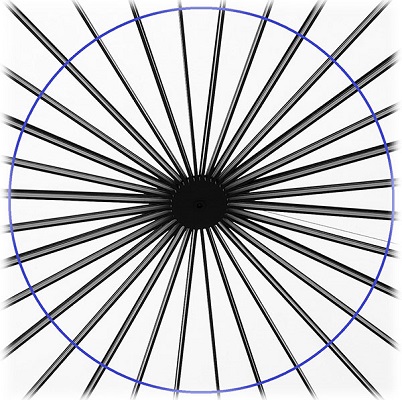
反射與對稱
物體及其映象
當物體放置在鏡子前時,會在鏡子上形成其映象。映象具有相同的高度、寬度和角度。
然而,物體和它的映象之間存在差異。也就是說,物體的左邊變成了映象的右邊,反之亦然。
例如,當我們在鏡子前舉起左手時,我們在映象中看到的是右手舉起。這種現象也被稱為**左右反轉**。
反射與對稱
原始物體及其映象彼此對稱,因此鏡子充當對稱軸。
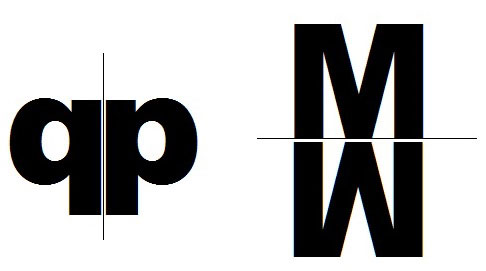
對稱的應用
對稱具有廣泛的應用。它在增強物體的美感方面起著重要作用。
Rangoli(印度傳統彩繪)
對稱的廣泛應用之一是Rangoli。使用對稱圖案製作的Rangoli,會產生美麗的圖案。

Rangoli可以有多條對稱軸,這增加了它們的美感。
紡織品
我們還可以在各種紡織品中看到對稱性。一些服裝嵌入了各種對稱圖案以增強其美感。

更多的對稱軸會產生更美麗的藝術作品。
紀念碑
世界上許多著名的建築和紀念碑都是利用各種形式的對稱性進行設計的。一些著名的例子包括泰姬陵、埃菲爾鐵塔、盧浮宮等。

很明顯,對稱物體比非對稱物體看起來更美。
製作對稱圖案
我們可以用簡單的方法建立對稱圖案。
墨跡魔鬼
可以使用墨跡在紙上繪製漂亮的對稱圖案。此過程稱為墨跡魔鬼。
- 取一張紙,對摺。
- 在一側滴幾滴墨水,然後將兩半壓在一起。
- 然後,展開紙張以檢視對稱圖案。
它的**對稱軸**將是紙張對摺的直線。
根據影像的型別,可能存在一條或多條對稱軸。

紙張對稱
有一種簡單的方法可以在紙上繪製對稱圖形。
- 取一張紙,對摺。
- 在紙張邊緣繪製一個形狀。
- 沿著圖案剪開紙張。
現在,開啟紙張以檢視對稱圖形。

萬花筒
這是一種圓柱形裝置,帶有鏡子,裡面包含不同顏色的物體,例如鵝卵石和玻璃碎片。當我們從一端觀看時,進入另一側的光線由於鏡子的反射而產生彩色的圖案。
