第6章 - 整數

正數

正數大於0。例如，5、11、87等數字位於0的右側，是正數。

負數

前面帶有負號或減號的數字稱為負數。例如，−4、−19、−112等數字位於0的左側，是負數。

0既不是正數也不是負數。

自然數

所有不包括分數的正數稱為自然數。自然數、零和負數統稱為**整數**。

整數在現實生活中的應用

溫度以攝氏度為單位測量，可以是正數或負數。水的冰點是0°C，低於此溫度則變為負數。因此，我們可以有−5°C、−21°C等溫度。

在電梯面板上，我們可以看到−1、−2、−3等負數。這裡我們將底層視為0，底層以下的樓層用負數表示。

在溫度計上，高於0度的溫度標記為正溫度，低於0度的溫度標記為負溫度。

我們使用正數表示利潤，使用負數表示虧損。例如，虧損20盧比可以認為是−20盧比。

數軸上整數的表示

自然數是1、2、3、4，依此類推。在數軸上，它們表示為

當我們向1的左側移動時，我們得到0，這組數字稱為**整數**。

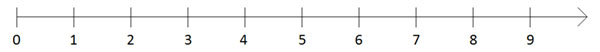
繼續向左移動，我們得到自然數的負數，即−1、−2、−3、−4，…

自然數、它們的負數和0一起構成**整數**集合。

垂直數軸

數軸也可以是垂直的，中間為0，正整數和負整數分別位於零的上方和下方。

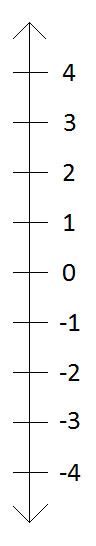
垂直數軸用於測量海拔高度和深度。這裡，平均海平面被視為參考點或0。

珠穆朗瑪峰的高度或海拔高度為平均海平面以上8,848米。
太平洋馬裡亞納海溝的深度約為−11,000米。

溫度計刻度就像一條垂直數軸。0度是中間的參考點。高於0度的溫度是高溫，低於0度的溫度是低溫。

比較整數

我們知道如何比較正整數。例如，

9 > 6 或 2 < 5

讓我們學習如何比較兩個負數。

**示例**：使用不等號（如<，>）比較2和5。

解答：比較數字的最佳方法是想象它們在數軸上的位置。

在數軸上，

位於右側的數字更大，並且
位於左側的數字更小。

例如，2位於5的左側，因此2 < 5。

同樣，5位於2的右側，因此，5 > 2。

**示例**：比較−2和−5。

解答：當我們在數軸上向0的左側移動時，我們看到−2位於−5的右側。

因此，−2 > −5。

或者，我們可以寫成−5 < −2。

升序和降序

當涉及兩個以上的數字時，我們在數軸上標記這些點，並從左到右排列這些數字。

如果數字從小到大排列，則稱為升序或遞增順序。
如果數字從大到小排列，則稱為降序或遞減順序。

**示例**：將數字−5、−3、0和1按升序和降序排列。

解答：首先在數軸上標記這些數字，如下所示。

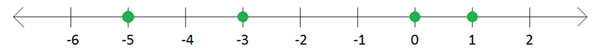
最左邊的數字−5是最小的，其他數字依次為−3、0和1。

升序

−5 < −3 < 0 < 1

降序

1 > 0 > −3 > −5

整數的加法

在數軸上向0的右側移動會增加值。這就像將兩個數字相加。

在數軸上向0的左側移動會減小數字的值，這就像將兩個數字相減。

兩個正整數相加

**示例**：計算3 + 5。

解答：從數軸上的3開始。

向右移動5個單位距離，落在數軸上的8上。

因此，我們有，

3 + 5 = 8

兩個負整數相加

**示例**：計算(−3) + (−5)

解答：從數軸上的−3開始。

向左移動5個單位距離，落在數軸上的−8上。

加法的結果，

−3 + (−5) = −8

一個正整數和一個負整數相加

**示例**：計算3 + (−5)

解答：從數軸上的3開始。

向左移動5個單位距離，落在數軸上的−2上。

結果是，

3 + (−5) = −2

三個或更多整數相加

**示例**：使用數軸計算(13) + (−7) + (−9)

解答：從數軸上13的位置開始。

由於要新增−7，因此向左移動7個單位。

13 + (−7) = 6

接下來，由於要進一步新增−9，因此從6向左移動9個單位。

6 + (−9) = −3

或者，

13 + (−7) + (−9) = −3

整數的減法

在數軸上向左移動就像進行減法。

正數（減）正整數

**示例**：從3中減去5。

解答：從3開始。向左移動5個位置。因此，

3 − 5 = −2

**示例**：(−3) + 5的結果是多少？

解答：從−3開始。由於有加號，因此向右移動5個單位。

結果是，

−3 + 5 = 2

正數（減）負整數

**示例**：考慮減法3 − (−5)。

解答：從一個正整數中減去一個負整數等價於將這兩個數字相加。

兩個減號放在一起構成一個加號。

(−) (−) = +

3 − (−5) = 3 + 5

從3開始，向右移動5個單位。結果是，

3 + 5 = 8

負數（減）負整數

**示例**：考慮減法(−3) − (5)。

解答：從另一個負整數中減去一個負整數等價於將這兩個數字相加，並在和前面加上一個負號。

從(−3)開始，然後向左移動5個單位。因此，

因此，

−3 − (5) = −3 − 5 = −8

三個或更多整數相減

示例

Question: Simplify −30 + 5 − (−17) − (−11)
Solution: It is known that
      (−) (−) = +
Rewriting the expression,
      −30 + 5 − (−17) − (−11)
      = −30 + 5 + 17 + 11
Adding all the positive integers,
      −30 + (5 + 17 + 11)
      = (−30) + 33
      = 3
The result is,
      −30 + 5 − (−17) − (−11) = 3

整數的乘法和除法

整數的乘法和除法類似於整數的乘法和除法，但有一些額外的步驟。

步驟如下

計算負號的數量。
忽略負號，執行數字的乘法或除法。
如果負號的數量為奇數，則結果為負數。
如果負號的數量為偶數，則結果為正數。

示例

Question: Solve −4 × 3
Solution: Number of negative integers = 1
Multiply the numbers, ignoring the negative sign,
      4 × 3 = 12
There are odd number of negative signs, so the product will be negative.
Thus, the answer is −12.

示例

Question: Solve (−4) × (−3)
Solution: The number of negative integers = 2
Ignore the negative signs and perform multiplication,
      4 × 3 = 12
There are even number of negative signs, so the product will be positive.
Thus, the answer is 12.

示例

Question: Solve (−9) ÷ 3
Solution: The number of negative integers = 1
Ignore the negative signs and perform division,
      9 ÷ 3 = 3
There are odd number of negative signs, so the quotient will be negative.
Thus, the answer is −3.

示例

Question: Solve (−9) ÷ (−3)
Solution: Count the number of negative signs: 2
Ignore the negative signs and perform the division of the numbers: 9 ÷ 3 = 3
There are even number of negative signs, so the quotient will be positive.
Thus, the answer is 3.

示例

Question: Solve (5 × 7) − (3 × 4 × −7)
Solution: Count the number negative signs in (3 × 4 × −7).
There is only 1 negative sign and it is odd
Ignore the sign and multiply to get,
      3 × 4 × 7 = 84
Since the number of negative signs is odd, the product is negative.
Rewriting the expression,
      (5 × 7) − (3 × 4 × −7)
      = 35 − (−84)
As (−) (−) = +,
      (5 × 7) − (3 × 4 × −7)
      = 35 − (−84)
      = 35 + 84
      = 119

列印頁面