第7章 - 分數

分數介紹

分數用兩個數字表示，一個在上，一個在下，用分隔線隔開。

分數的型別

根據分子是否大於分母，分數可以分為兩種型別。

分數的轉換

假分數和帶分數是同一數量的兩種不同表示方法。

數軸上分數的表示

就像整數一樣，分數也可以在數軸上表示。

問題

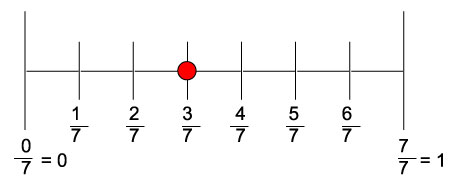
在數軸上表示真分數${3}/{7}$。

解答

分數的分母 = 7 所以，將0和1之間的間隔分成七個相等的部分。

等於分子值（即3）的部分等於真分數。所以，分數${3}/{7}$可以表示如下

數軸上假分數的表示

帶分數是在兩個整數之間的一個數。換句話說，它是一個整數和一個整體的一部分。

要表示假分數，

• 首先將假分數轉換為帶分數。
• 在帶分數中，整數部分表示該數後面的整數。

例子：在數軸上表示分數3${4}/{7}$。

解答:

3${4}/{7}$將位於整數3和4之間。

接下來，將間隔分成七個相等的部分（與分母相同）。

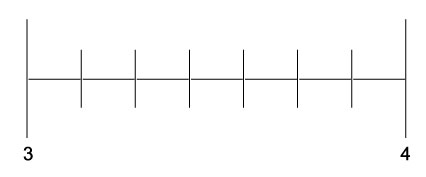
它們被編號為

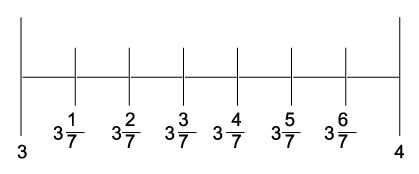
所以，3${4}/{7}$將是3個整體和3和4之間整體的第4部分。

等值分數

等值分數看起來不同，但它們的值相同或表示相同的數量。

例如，${2}/{4}$和${3}/{6}$在數軸上表示相同的點。它們是等值分數。

同樣，${3}/{7}$，${6}/{14}$，${9}/{21}$……是等值分數，它們都表示相同的數量${3}/{7}$。

尋找等值分數

要找到給定分數的等值分數，將原分數的分子和分母乘以或除以相同的數。

例子：找出${1}/{4}$的等值分數

解答:

${1}/{4}$的一些等值形式是

• ${1 × 2}/{4 × 2}$ = ${2}/{8}$
• ${1 × 3}/{4 × 3}$ = ${3}/{12}$
• ${1 × 4}/{4 × 4}$ = ${4}/{16}$
• ${1 × 5}/{4 × 5}$ = ${5}/{20}$

例子：找出${3}/{8}$的等值分數

解答:

${3}/{8}$的一些等值形式是

• ${3 × 2}/{8 × 2}$ = ${6}/{16}$
• ${3 × 3}/{8 × 3}$ = ${9}/{24}$
• ${3 × 4}/{8 × 4}$ = ${12}/{32}$
• ${3 × 5}/{8 × 5}$ = ${15}/{40}$

分數的簡化

分數${6}/{12}$可以用較大的數字表示為${100}/{200}$，也可以用較小的數字表示為${1}/{2}$。分數的簡化是尋找分數最簡等值形式的過程。

分數的最簡形式定義為分子和分母除了1以外沒有其他公因數的分數。例如，${2}/{3}$，${5}/{9}$，${23}/{97}$等等。

第一種方法

要找到分數的最簡形式，可以透過用相同的數去除分子和分母來找到它的等值形式。

例子：簡化分數${9}/{36}$。

解答:

由於9和36有公因數3，則一個簡化形式為

$${9}/{36} = {9}/{3} \: / \: {36}/{3} = {3}/{12}$$

3和12有公因數3，所以將繼續簡化

$${3}/{12} = {3}/{3} \: / \: {12}/{3} = {1}/{4}$$

由於1和4除了1以外沒有公因數，所以這是原分數的最簡形式。

第二種方法

我們可以透過用兩個數的最大公因數（HCF）去除分子和分母來找到分數的最簡形式。

例子：簡化分數${9}/{36}$

解答:

讓我們找出數字9和36的最大公因數。

因此，9和36的最大公因數是9。

用最大公因數去除分子和分母，

$${9}/{36} = {9}/{9} \: / \: {36}/{9} = {1}/{4}$$

${1}/{4}$是最簡形式的分數。

同分母分數和異分母分數

同分母分數

具有相同分母的分數稱為同分母分數。例如，

$${2}/{7}, {5}/{7}, {14}/{7}, {236}/{7}$$

是同分母分數，因為它們具有相同的分母“7”。

異分母分數

具有不同分母的分數稱為異分母分數。例如，

$${23}/{3}, {322}/{12}, {56}/{531}, {12}/{4}$$

是異分母分數，因為每個分數都有不同的分母。

例子：在一個生日聚會上，一個蛋糕被切成20個相等的部分。三個朋友分別得到5塊、2塊和1塊。朋友們分別得到了多少蛋糕？

解答:

朋友們得到的蛋糕分數是${5}/{20}$，${2}/{20}$和${1}/{20}$。

這些是同分母分數。

例子：如果將前面例子中的分數，即${5}/{20}$，${2}/{20}$和${1}/{20}$簡化為最簡形式，則得到${1}/{4}$，${1}/{10}$和${1}/{20}$。這些是什麼型別的分數？

解答:

分數${1}/{4}$，${1}/{10}$和${1}/{20}$的分母是不同的。

這些是異分母分數。

例子：將下列分數分類為同分母分數和異分母分數。

$${1}/{2}, {7}/{4}, {3}/{2}, {9}/{11}, {5}/{2}, {13}/{6}$$

解答:

在給定的分數中，

${1}/{2}$，${3}/{2}$，${5}/{2}$是同分母分數，因為它們具有相同的分母2。

${7}/{4}$，${9}/{11}$，${13}/{6}$是異分母分數，因為它們具有不同的分母。

分數的比較

同分母分數的比較

同分母分數的比較很簡單，因為它們的分母相同。要比較兩個同分母分數，只需比較它們的分子。

例：比較分數 ${2}/{7}$ 和 ${3}/{7}$

解答:

分數 ${2}/{7}$ 和 ${3}/{7}$ 有相同的分母。所以，由於 2 < 3，我們可以說 ${2}/{7}$ < ${3}/{7}$。

異分母分數的比較

要比較兩個異分母分數，

• 首先將異分母分數轉換為具有相同分母的等值同分母分數。
• 然後，比較等值分數的分子。

分數的分母透過乘法/除法轉換為它們的最小公倍數 (LCM)。

相應的分子乘以相同的數字，從而得到具有相同分母的等值分數。

例：比較分數 ${2}/{3}$ 和 ${5}/{7}$

解答:

我們有兩個異分母分數：${2}/{3}$ 和 ${5}/{7}$

讓我們使用等值分數將它們轉換為同分母分數。

兩個分母 3 和 7 的最小公倍數 = 21。

因此，等值分數將具有 21 作為分母。

轉換第一個分數

$${2 × 7}/{3 × 7} = {14}/{21}$$

轉換第二個分數

$${5 × 3}/{7 × 3} = {15}/{21}$$

現在，比較等值同分母分數的分子。

由於 14 < 15，

$${14}/{21} < {15}/{21} \: 或 \: {2}/{3} < {5}/{7}$$

例：比較 ${4}/{5}$ 和 ${16}/{20}$

解答:

我們有兩個異分母分數：${4}/{5}$ 和 ${16}/{20}$

分母 5 和 20 的最小公倍數 = 20

因此，等值分數將具有 20 作為分母。

轉換第一個分數

$${4 × 4}/{5 × 4} = {16}/{20}$$

轉換第二個分數

$${16 × 1}/{20 × 1} = {16}/{20}$$

現在，比較等值同分母分數的分子。

兩個數字都具有相同的分子和分母，因此

$${4}/{5} = {16}/{20}$$

分數的加法和減法

同分母分數的加法和減法

分數的加法與整數的加法不同。在加或減同分母分數時，分母保持不變，分子相加或相減。

例：加分數 ${3}/{16}$ + ${7}/{16}$

解：在加同分母分數時，只需將分子相加，保持分母不變。

$${3}/{16} + {7}/{16} = {3 + 7}/{16} = {10}/{16}$$

例：減分數 ${8}/{19}$ − ${7}/{19}$

解：在減同分母分數時，只需將分子相減，保持分母不變。

$${8}/{19} − {7}/{19} = {8 − 7}/{19} = {1}/{19}$$

異分母分數的加法和減法

在加或減異分母分數時，

• 首先將它們轉換為同分母分數，
• 然後將分子相加或相減，
• 分母保持不變。

例：加 ${3}/{8}$ + ${7}/{6}$

解答:

我們有兩個異分母分數，

$${3}/{8} \: 和 \: {7}/{6}$$

讓我們首先將它們轉換為同分母分數。

分母 8 和 6 的最小公倍數 = 24

因此，公分母將是 24。

${3}/{8}$ 和 ${7}/{6}$ 的等值同分母分數是

$${3}/{8} = {(3 × 3)}/{(8 × 3)} = {9}/{24}$$

$${7}/{6} = {(7 × 4)}/{(6 × 4)} = {28}/{24}$$

將分子相加，保持分母不變。

$${3}/{8} + {7}/{6} = {9}/{24} + {28}/{24} = {37}/{24}$$

例：減 ${7}/{6}$ − ${3}/{8}$

解答:

6 和 8 的最小公倍數 = 24

公分母將是 24

減去它們的等值同分母分數，

$${7}/{6} − {3}/{8} = {(7 × 4)}/{(6 × 4)} − {(3 × 3)}/{(8 × 3)}$$

$$ = {28}/{24} − {9}/{24} = {28 − 9}/{24}$$

$$ = {19}/{24}$$

加法和減法的特殊情況

整數加真分數

任何整數除以 1 等於它本身。例如，

$${12}/{1} = 12 \: 和 \: {4}/{1} = 4$$

因此，任何整數都可以透過將其分母設為 1 來表示為分數。

例：加 9 + ${2}/{7}$

解答:

$$9 + {2}/{7} = {9}/{1} + {2}/{7}$$

但這些是異分母分數。

讓我們將它們轉換為同分母分數。

$${9}/{1} = {9 × 7}/{1 × 7} = {63}/{7}$$

同樣地，

$${2}/{7} = {2 × 1}/{7 × 1} = {2}/{7}$$

現在加上同分母分數，

$${63}/{7} + {2}/{7} = {63 + 2}/{7} = {65}/{7}$$

將假分數轉換為帶分數，

$${65}/{7} = 9{2}/{7}$$

另一種方法

要加一個整數和一個真分數，去掉問題中的加號，將其寫成帶分數。例如，

$$9 + {2}/{7} = 9{2}/{7}$$

$$5 + {3}/{11} = 5{3}/{11}$$

整數減真分數

整數表示為分母為 1 的分數。

將異分母分數轉換為同分母分數，然後相減以獲得結果。

例：加 9 − ${2}/{7}$

解答:

$$9 − {2}/{7} = {9}/{1} − {2}/{7}$$

${9}/{1}$ 和 ${2}/{7}$ 的同分母分數是 ${63}/{7}$ 和 ${2}/{7}$

減去同分母分數，

$${63}/{7} − {2}/{7} = {63 − 2}/{7} = {61}/{7}$$

將假分數轉換為帶分數，

$${61}/{7} = 8{5}/{7}$$