
第10章 - 測量
測量學導論
我們使用不同的單位來測量不同的東西。例如,為了測量時間,我們使用分鐘、秒和小時。同樣,為了測量距離,我們使用公里、米等。
事實上,有一個專門的分支叫做計量學,專門處理測量問題。
什麼是測量學?
測量學是幾何學的一部分,它涉及到對不同幾何形狀及其測量的研究。我們使用測量學來計算不同幾何形狀的長度、寬度、深度、面積和體積。
幾何形狀有兩種型別:2D 和 3D。
2D 形狀
2D 形狀由三條或多條直線或平面上的封閉圓圈包圍。它們有兩個維度:長度和寬度,因此被稱為 2D 圖形或形狀。對於 2D 形狀,我們測量面積和周長。
2D 形狀的例子包括圓形、矩形、正方形、三角形、梯形等。
3D 形狀
3D 形狀由多個平面包圍。這些也被稱為立體形狀。
除了長度和寬度之外,3D 形狀還有高度(或深度)。
一些眾所周知的 3D 形狀:立方體、圓錐體、稜錐體、圓柱體、稜柱體和長方體。

周長
封閉曲線的邊界長度稱為周長。我們無法找到開放曲線的周長。
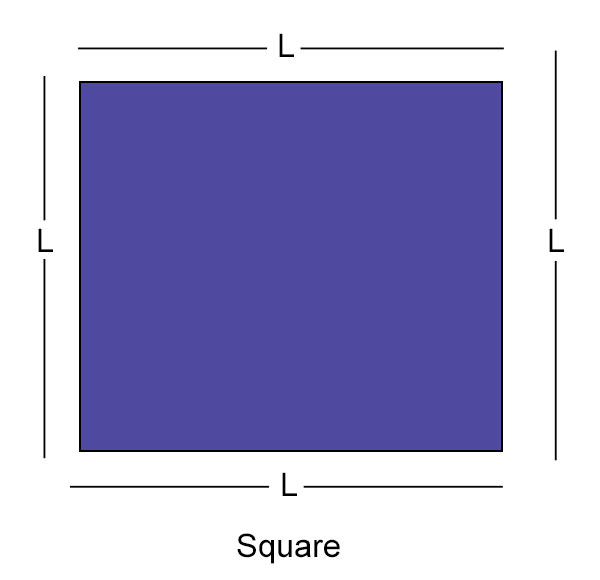
正方形的周長
正方形有四條相等邊。因此,我們有以下公式:
正方形的周長 = 其各邊的和
將每條邊的長度表示為 L,周長表示為 P,
P = 4 × L
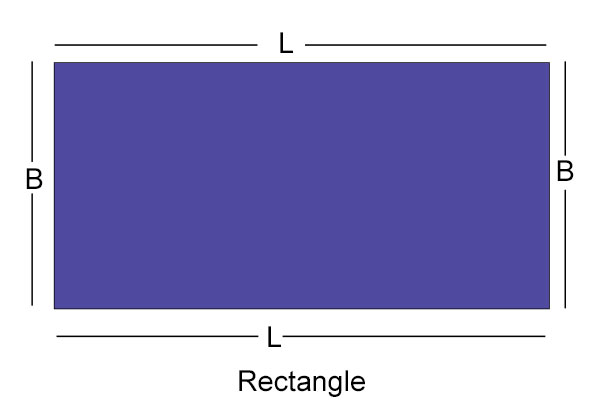
矩形的周長
矩形的對邊相等。
設 L = 長度,B = 寬度,則其周長為:
P = L + L + B + B
或 P = 2L + 2B
規則多邊形的周長
如果所有邊和角都相等,則多邊形稱為規則多邊形。
假設 L = 每條邊的長度,
等邊三角形的周長 = 3 × L = 3L
正方形的周長 = 4 × L = 4L
正五邊形的周長 = 5 × L = 5L
正六邊形的周長 = 6 × L = 6L
規則多邊形的周長是它具有的邊數乘以每條邊的長度。因此,
P = n × L
其中“n”是規則多邊形的邊數。
矩形和正方形的面積
矩形和正方形是兩種廣泛使用的規則形狀。我們可以使用方格紙或格點紙來找到矩形或正方形的面積。
矩形的面積
矩形的對邊長度相等。矩形的較長邊稱為長度,較短邊稱為寬度。
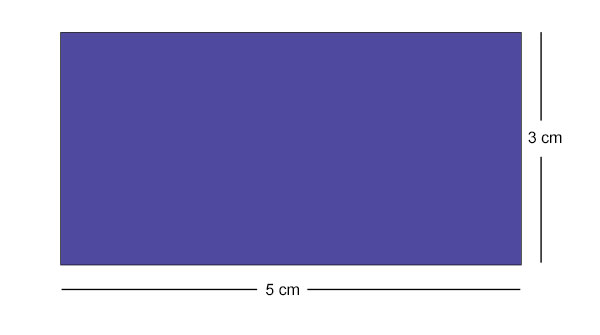
讓我們使用方格紙來找到它的面積。

矩形包含了 15 個完整的方格。
每個方格的尺寸為 1 平方釐米。
因此,矩形的面積為 15 平方釐米。
觀察到,
15 平方釐米 = (5 釐米 × 3 釐米) = (長度 × 寬度)
由此,我們可以得出結論,
矩形的面積 = (長度 × 寬度)
示例
A rectangle has a length of 8 cm and a breadth 5 cm. What is its area?
Area of the rectangle = Length × breadth
= 8 cm × 5 cm
= 40 sq. cm.
正方形的面積
正方形的四條邊長度相等。
讓我們取一個邊長為 8 釐米的正方形,並找到它的面積。

在方格紙上繪製正方形。
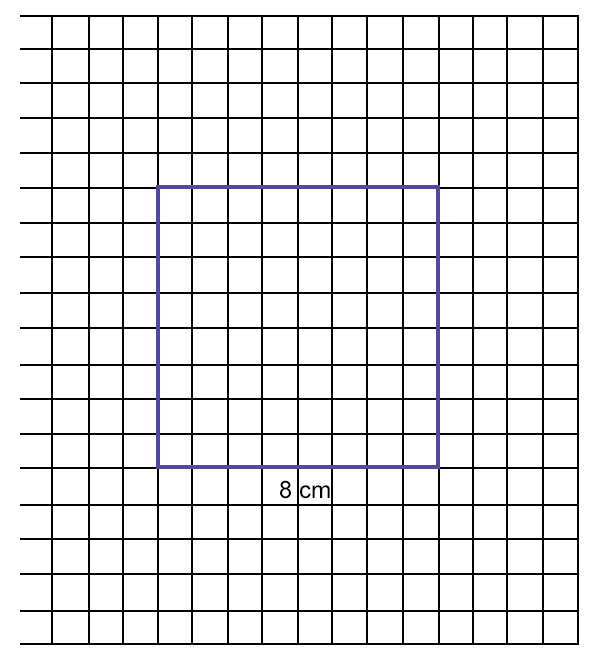
正方形包含了 64 個完整的方格。因此,它的面積為 64 平方釐米。
觀察到,正方形的面積為:
64 平方釐米 = (8 釐米 × 8 釐米) = (邊長 × 邊長)
我們可以得出結論,
正方形的面積 = 邊長 × 邊長
示例
A square has a side of length 10 cm. Find its area.
Area of the square = Side × Side
= 10 cm × 10 cm
= 100 sq. cm.
不規則圖形的面積
圖形邊界內包含的區域稱為其面積。我們通常使用方格紙(或格點紙)來找到規則和不規則圖形的面積。
如何使用方格紙?
有一些關於如何使用方格紙來找到封閉圖形的面積的規則。
- 完全覆蓋的方格 = 1 平方單位
- 覆蓋 ${1}/{2}$ 的方格 = ${1}/{2}$ 平方單位
- 覆蓋少於 ${1}/{2}$ 的方格 = 0 平方單位
- 覆蓋多於 ${1}/{2}$ 的方格 = 1 平方單位
不規則圖形的面積
讓我們使用上述規則來找到不規則圖形的面積。
示例:使用方格紙找到給定圖形的面積。

解答:讓我們繪製圖形的輪廓,並計算完全覆蓋、${1}/{2}$ 覆蓋、多於和少於 ${1}/{2}$ 覆蓋的方格的數量。

現在,讓我們應用規則來計算面積
| 覆蓋面積 | 數量 | 面積(平方單位) |
|---|---|---|
| 完全覆蓋 | 2 | 2 × 1 = 2 |
| ${1}/{2}$ 覆蓋 | 1 | 1 × ${1}/{2}$ = ${1}/{2}$ |
| 多於 ${1}/{2}$ 覆蓋 | 4 | 4 × 1 = 4 |
| 少於 ${1}/{2}$ 覆蓋 | 7 | 7 × 0 = 0 |
總面積 = 2 + ${1}/{2}$ + 4 = 6${1}/{2}$ 平方單位。