第14章 - 實踐幾何

實踐幾何簡介

從像桌子和書這樣的基本物體到世界著名的紀念碑，一切都可以用它們的幾何形狀來定義。

幾何盒

我們可以藉助幾何盒中提供的工具繪製基本幾何圖形，如線段、三角形、矩形和圓形。

尺子 - 使用此工具繪製均勻的線段。
圓規 - 使用此工具比較兩條線段的長度。
圓規 - 繪製弧線或圓形
三角板 - 繪製三角形或垂直線
量角器 - 測量角度
其他（鉛筆、橡皮擦、卷筆刀） - 使用這些工具進行繪圖。

幾何思想體現在所有形式的藝術、測量、建築、工程和設計中。

線段和圓的作圖

可以使用尺子繪製線段，可以使用圓規繪製圓形。

繪製線段

要使用尺子繪製線段，

考慮我們選擇的長度，例如 10 釐米。
取尺子，從 0 釐米到 10 釐米繪製一條線段。

我們還可以使用尺子來測量和比較不同線段的長度。

比較兩條線段

我們使用圓規來比較不同線段的長度。

將圓規兩腳的尖端固定線上段的兩端。
兩腳之間的間隙越大，線段越長。

也可以使用圓規和尺子來測量線段的長度。

使用圓規繪製圓形

讓我們將圓的半徑固定為 4 釐米。

取一把尺子，將圓規的兩臂伸展，使一隻臂固定在 0 處，另一隻臂固定在 4 釐米處。
用手握住圓規頂部，並將圓規的另一臂牢牢地固定在紙上，然後旋轉鉛筆臂。

這樣，我們就繪製了一個半徑為 4 釐米的完美圓形。

垂直線的作圖

與另一條線成 90° 角的線稱為該線的垂線。可以使用三角板或圓規繪製垂直線。

有四種方法可以繪製垂直線。

方法 1 - 使用尺子和三角板

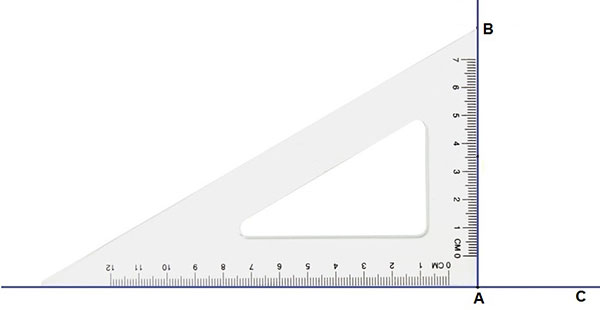
畫一條線 c 並在其上標記一個點 A。
將尺子的一條邊沿 l 放置。
將三角板放在線上，使其 90° 朝向的邊與線重合。
沿著尺子的邊緣滑動三角板，直到其直角角與 A 重合。
在三角板與 A 重合的地方畫一條想要的線，並將其端點命名為 B。
新線 AB 垂直於線 c。

方法 2 - 使用尺子和三角板

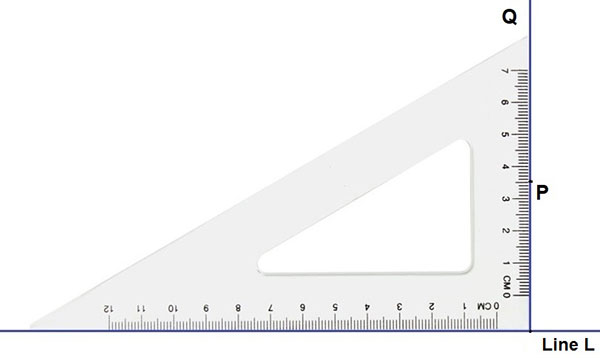
畫一條直線 l 並在其外部標記一個點 P。
將三角板放在 l 上，使其直角的一條邊與 l 對齊。
將尺子放在三角板直角對面的邊上。
固定尺子，然後沿尺子滑動三角板直到點 P。
當直角接觸到點 P 時停止滑動。
畫一條連線點 P 到線 l 的線段。

方法 3 - 使用尺子和圓規

畫一條線 l 並在其上標記一個點 P。
取圓規並選擇一個合適的半徑。
以 P 為圓心，使用圓規繪製一條弧線。
該弧線應與線 l 相交於兩點 A 和 B。
以 A 和 B 為圓心，以大於 AP 的半徑繪製兩條弧線，它們相交於 Q。
連線 PQ 以獲得所需的垂線。

方法 4 - 使用尺子和圓規

畫一條線 l 並在其外部標記一個點 P。
以 P 為圓心，畫一條弧線，該弧線與線 l 相交於兩點 A 和 B。
使用相同的半徑，以 A 和 B 為圓心，再繪製兩條弧線，它們在另一側相交於一點，例如 Q。
連線 PQ 以獲得所需的垂線。

垂直平分線的作圖

“平分”一詞表示分成兩等份。

如果我們使用一條垂直線將一條線分成兩等份，那麼這條垂直線稱為垂直平分線。

繪製垂直平分線

畫一條任意長度的線段 AB。
以 A 和 B 為圓心，用圓規在 AB 兩側繪製四條弧線，使它們相交於兩點。
將這兩個點命名為 P 和 Q。
半徑應大於 AB 長度的一半。
連線點 P 和 Q。它在 O 處與 AB 相交。
PQ 是 AB 的垂直平分線。

在上圖中，

AO = OB = ${1}/{2}$AB

您可以使用尺子驗證 AO = OB。

角的作圖

由兩條從一個共同點（頂點）發散的線或射線形成的圖形稱為角。

角可以具有不同的度數，例如 40°、60°、90°、180° 等。

使用量角器繪製角

假設我們要繪製一個 40° 的銳角。

我們使用量角器繪製角。

步驟如下

畫一條任意長度的線段 AB。
取量角器，將其中心放在點 A 上。
量角器的 0° 刻度應與線段 AB 重合。
現在，使用量角器標記 40°。將此點命名為 C。
由於線段落在中心的右側，因此標記右側的 40°。
連線點 A 和 C。
∠BAC 是所需的角。

如果線段位於中心的左側，則我們將標記量角器左側的 40°。

角平分線的作圖

角平分線是將一個角分成兩個相等部分的線。例如，60° 角的平分線將產生兩個各為 30° 的角。

繪製角平分線

步驟如下

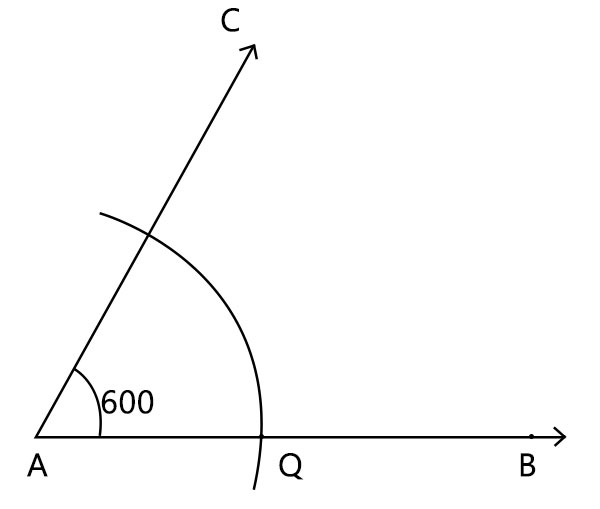
假設我們有一個角 ∠A。
取圓規，選擇您選擇的合適半徑，並以 A 為圓心繪製一條弧線
該弧線應與 ∠A 的兩條邊相交。
將交點標記為 P 和 Q。

使用相同的半徑，以 P 和 Q 為圓心，繪製兩條弧線，使它們在一點（∠A 的內部）處相交。

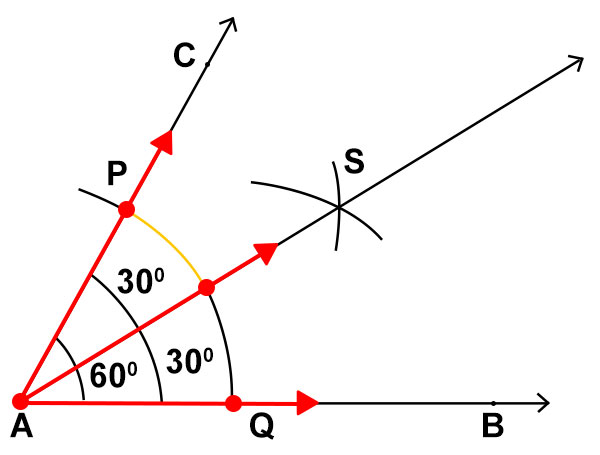
將交點命名為 S。
連線點 A 和 S。
線段 AS 是 ∠A 的角平分線。

AS 將角 ∠A 平分成兩個相等的部分。

列印頁面