
第3章 - 玩轉數字
玩轉數字 (引言)
乘法作為重複加法
乘法是重複加法。如果一個數字被重複加幾次,那麼你可以簡單地用它被加的次數乘以它。
示例
Adding 5 to itself 8 times to get 40 is same as multiplying 5 by 8 to get 40.
5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 40
Or,
5 × 8 = 40
因數和倍數
讓我們重新回顧一下乘法表
5 × 1 = 5
5 × 2 = 10
5 × 3 = 15
等號左邊的數字稱為因數,右邊的數字稱為倍數。
例如,在…的情況下
5 × 3 = 15
5和3是因數,15是倍數。
除法作為重複減法
除法是重複減法。
示例
If 4 is subtracted from 16 repeatedly for 4 times, we get zero at the end.
This is same as dividing 16 by 4.
16 − 4 − 4 − 4 − 4 = 0
Or,
16 ÷ 4 = 0
一個數(被除數)的精確除法是連續減去一個數(除數),直到得到零(餘數)。
因數和倍數
什麼是倍數?
X 的倍數是透過將X乘以其他數字(1, 2, 3, 4, 5...)獲得的結果數字。任何數字的倍數都是無限的。
示例
Consider the multiplication table of 3:
3 × 1 = 3
3 × 2 = 6
3 × 3 = 9
3 × 4 = 12
3 × 5 = 15
...........
將3乘以不同的數字獲得的結果數字,即3、6、9、12和15,稱為3的倍數。
什麼是因數?
X 的因數是一個能完美地整除X的數字。例如,3是12的因數,因為它能完美地整除12(沒有餘數)。
示例
Which of the two, 5 or 7, is a factor of 30?
30 ÷ 5
30 ÷ 7
In the first case,
30 ÷ 5 = 6
5 perfectly divides 30 with 0 as remainder and 6 as quotient. So 5 is a factor of 30.
In the second case,
30 ÷ 7
Produces a remainder 2. As 7 does not perfectly divide 30, it is not a factor of 30.
倍數與因數相反
讓我們舉個例子
3 × 9 = 27
在這種情況下,27是3和9的倍數。
同時,3和9是27的因數,因為它們都能完美地整除27。
有趣的事實
- 每個數字都是它自身的倍數。
- 每個數字都是它自身的因數。
- 一個數字的因數是有限的,而一個數字的倍數可以是無限的。
- 一個數字的每個因數都小於或等於該數字。
- 一個數字的每個倍數都大於或等於該數字。
- 1是所有數字的公因數。
質數和合數
質數
只有兩個因數的數字稱為質數。換句話說,質數只能被1和它自身整除。
例如,2、3、5、7、11...是質數。這些數字只有兩個因數:1和它們自身。
合數
有超過兩個因數的數字稱為合數。例如,4、6、8、9、10...是合數。
注意:數字1既不是質數也不是合數。
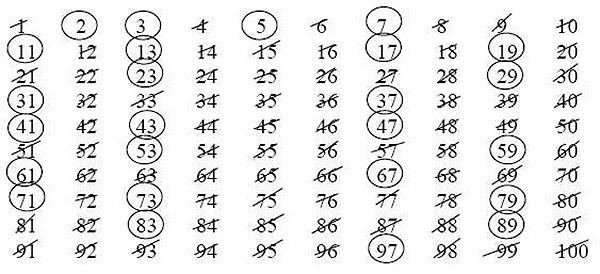
埃拉托色尼篩法
為了找到1到100之間的質數和合數,我們將使用倍數的概念而不是因數的概念。
一位希臘數學家埃拉托色尼使用倍數的概念來篩選出1到100之間的質數和合數。
- 在數字列表中,1既不是質數也不是合數,所以1被排除在外。
- 我們轉到1後面的數字,即2。列表中所有2的倍數,如4、6、8、10、12...都被劃掉。
- 我們轉到2後面的數字,即3,它沒有被劃掉。所有3的倍數,如6、9、12、15...都被劃掉。
- 我們移動到下一個沒有被劃掉的數字,即5。所有5的倍數,如10、15、20、25...都被劃掉。
- 請注意,在3之後,我們跳到5,因為4已經被劃掉了,因為它是的2的倍數。
- 這個過程重複進行,直到所有數字都被圈出或劃掉。
被圈出的數字是質數,所有被劃掉的數字都是合數。
偶數和奇數
偶數
所有能被2整除或是的2的倍數的數字都稱為偶數。
現在讓我們學習另一種根據數字末位數字或個位數字對數字進行分類的方法。
考慮一些2的倍數
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22 ....
我們在這裡看到一個模式。所有這些數字的末位數字都是0、2、4、6、8。
因此,所有以2、4、6、8或0結尾的數字都稱為偶數。
示例
450 is even, as it ends in a 0. 4986 is even number, as it ends in a 6. What about 9,99,998? This too is even, as it has 8 at the end.
奇數
以1、3、5、7或9結尾的數字稱為奇數。
奇數也定義為不能被2整除或不是2的倍數的數字。
考慮數列
1, 3, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25 ...
在這裡,我們看到一個模式,這些數字的末尾數字是1、3、5、7或9。正如我們已經定義的那樣,這樣的數字稱為奇數。
示例
789 is odd, as it ends with 9. Similarly, 4515 is odd, as it ends with 5. Let's take 673421821. This too is odd, as it ends with 1.
數字的可除性檢驗
2的可除性規則
如果一個數字以0、2、4、6或8結尾,則該數字能被2整除。
示例
Consider the number, 486. Since its last digit is 6, it is divisible by 2. Consider another number, 789. Its last digit is 9. So, 789 is not divisible by 2.
3和9的可除性規則
3和9的可除性規則相似。
- 將數字的各位數字加起來。
- 如果和是3的倍數,則該數字本身能被3整除。
示例
Consider the number, 486. Sum of digits, 4 + 8 + 6 = 18 18 is a multiple of 3. So, 486 is divisible by 3. 18 is a multiple of 9. So, 486 is divisible by 9 too. Now, consider another number, 29. Sum of digits, 2 + 9 = 11 11 is neither a multiple of 3 nor 9. So, 29 is neither divisible by 3 nor 9.
6的可除性規則
如果一個數字能被2和3整除,則它能被6整除。
示例
486 is divisible by both 2 and 3. Hence, 486 is divisible by 6 too! Let's take 488. It's divisible by 2, but not by 3. So, 488 is not divisible by 6.
4的可除性規則
如果一個兩位或多位數的最後兩位數字(從左向右數)能被4整除,則該數字能被4整除。
示例
Consider 552. 52 is divisible by 4. So, 552 is divisible by 4. What about 8261? 61 is not divisible by 4. So, 8261 is not divisible by 4.
8的可除性規則
如果一個三位或多位數的最後三位數字(從左向右數)能被8整除,則該數字能被8整除。
示例
Consider 5,55,552. The number formed by last three digits is 552. 552 is divisible by 8. So, 5,55,552 is divisible by 8.
5的可除性規則
如果一個數字以0或5結尾,則它能被5整除。例如,790和795能被5整除。
10的可除性規則
這是最簡單的可除性規則。如果一個數字只以0結尾,則它能被10整除。例如,790能被10整除,但795不能。
11的可除性規則
如果一個數字的偶數位數字之和與奇數位數字之和的差是0或11的倍數,則該數字能被11整除。
示例
Consider the number, 4565. Sum of digits in even places = 6 + 4 = 10 Sum of digits in odd places = 5 + 5 = 10 Difference of sums = 10 − 10 = 0 So, the number 4565 is divisible by 11.
公因數和公倍數
公因數
因數是能完美地整除一個給定數字的數字。例如,8的因數是1、2、4和8。
兩個或多個數字可以有很多共同點;例如,因數。
示例
Consider the numbers, 15 and 20. Factors of 15 are: 1, 3, 5, 15 Factors of 20 are 1, 2, 4, 5, 10, 20 The common factors of 15 and 20 are 1 and 5. Factor 1 is trivial, as it a factor of every number.
示例
Consider the numbers, 12 and 24 Factors of 12 are: 1, 2, 3, 4, 6, 12 Factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24 The common factors of these two numbers are 1, 2, 3, 4, 6, and 12.
互質數
只有1作為公因數的數字稱為互質數。例如,9和10是互質數。
同樣,215和216是互質數,因為它們唯一的公因數是1。
公倍數
一個數字(X)的倍數是我們用X乘以其他數字(如1、2、3、4...)得到的數字。例如,8、16、24、32...是8的倍數。
示例
Consider the multiples of the numbers, 4 and 8. Multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32... Multiples of 8 are: 8, 16, 24, 32... The common multiples of 4 and 8 are 8, 16, 24.... Common factors and common multiples are useful in understanding the concept of LCM and HCF.
質因數分解
什麼是質因數分解?
眾所周知,合數可以表示為其因數的乘積。
例如,合數20可以表示為:
4 × 5 = 20
2 × 10 = 20
因數4可以進一步表示為
2 × 2 = 4
同樣,10可以進一步分解為
2 × 5 = 10
這樣,我們將合數表示為其質因數的乘積。例如:
36 = 2 × 2 × 3 × 3
和
45 = 3 × 3 × 5
這個將一個數字分解為其質因數的過程稱為質因數分解。
示例
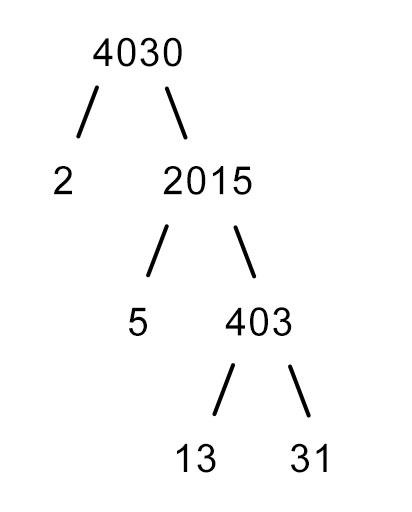
Question: Find the prime factorization of 4030. Solution: Using divisibility rules, we know that 4030 is divisible by 2 4030 ÷ 2 = 2015 2015 is not divisible by 3 because 2 + 0 + 1 + 5 = 8 And, 8 is not divisible by 3. However, 2015 is divisible by 5, as it ends with 5. 2015 ÷ 5 = 403 Trying out different numbers, it is found that 403 is divisible by 13. 403 ÷ 13 = 31 13 and 31 are prime numbers. Factorization ends here. Hence, we can express 4030 as, 4030 = 2 × 5 × 13 × 31 2, 5, 13, and 31 are the prime factors of 4030.
因數樹
可以使用因數樹的概念將一個數字表示為其質因數的形式。
4030的因數樹如下所示
用質因數分解法求最大公因數
定義:兩個或多個數字的最大公因數(HCF)是能完美地整除這些數字的最大數字。
我們可以使用質因數分解法來找到兩個或多個數字的最大公因數。
示例
Question: Find the HCF of 5, 10, and 15. Solution: 5 = 1 × 5 10 = 2 × 5 15 = 3 × 5 The common factor among these is 5 and it is the highest as well. Hence 5 is the HCF of 5, 10, and 15.
示例
Question: Find the HCF of 4, 8, and 16. Solution: 4 = 2 × 2 8 = 2 × 2 × 2 16 = 2 × 2 × 2 × 2 The HCF of these three numbers is = 2 × 2 = 4.
示例
Find the HCF of the numbers 14, 15, and 16. Solution: 14 = 2 × 7 15 = 3 × 5 16 = 2 × 2 × 2 × 2 There is no common factor except 1 for these numbers. Hence, 1 is the HCF of 14, 15, and 16.
用輾轉相除法求最大公因數
除了質因數分解法之外,還有一種方法可以找到兩個或多個數字的最大公因數。它被稱為輾轉相除法。
讓我們用例子來理解這個方法。
示例:求8、28和32的最大公因數。
解答:讓我們取前兩個數字8和28。
用8除28→餘數是4。
接下來,將除數(8)向下移動,並用餘數(4)除以它。
重複此過程,直到餘數為0。
記下產生餘數為0的除數。
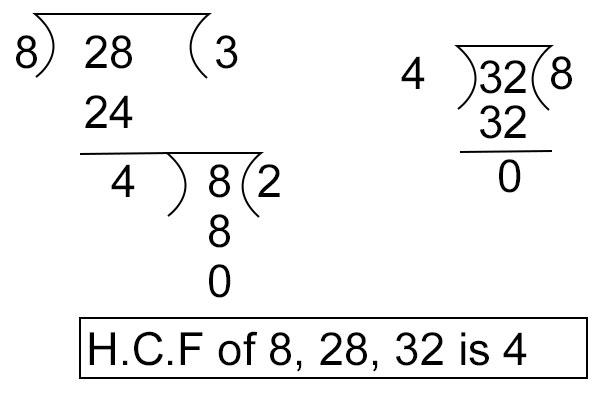
8和28的最大公因數是4。
接下來,取第三個數32,並用4除以它。
我們得到餘數為0。
因此,4是8、28和32的最大公因數。
理解最小公倍數
定義:最小公倍數(LCM)是兩個或多個數字的所有倍數中最小的倍數。
有兩種方法可以找到一組數字的最小公倍數
- 梯形法
- 質因數分解法
梯形法
- 將需要求最小公倍數的數字寫成以逗號分隔的序列。
- 用能整除最多數字的最小質數來除這組數字。
- 不能整除的數字作為餘數向下移動。
- 再次選擇一個質數作為除數,併除以所有餘數。
- 重複此過程,直到數字沒有任何公因數。
- 在除法過程中會形成一個數字梯。
- 然後,梯形外部數字的乘積給出給定數字的最小公倍數。
示例:使用梯度法求4、9和16的最小公倍數。
取最小的質數2,可以看到它可以整除三個數中的兩個,即4和16。由於9不能被2整除,因此將其直接向下移。再次取一個可以整除這些數的質數(2)作為除數,進行除法運算,得到1、9和4。至少有兩個數沒有相同的因子。
然後,梯形外部所有數字的乘積就是最小公倍數。
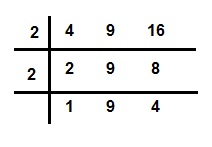
所以最小公倍數 = 2 × 2 × 9 × 4 = 144
質因數分解法
每個數字都可以表示為一個或多個質數的乘積。
在這種方法中,一組數字的最小公倍數是透過使用每個數字的質因數來找到的。
找到每個質因數出現的最大次數,這些數字的乘積就是最小公倍數。
示例
Question: Find the LCM of 6, 9, and 15. Solution: In prime factorization method, the numbers are written as product of their prime factors. 6 = 2 × 3 9 = 3 × 3 15 = 3 × 5 Prime factor 2 occurs only once in 6. The maximum number of times 2 occurs is only 1. Prime factor 3 occurs in all the three numbers, but it occurs twice in 9. It's the maximum. So, 3 is taken twice. Prime factor 5 occurs only once in 15. So, the LCM of 6, 9, and 15 is, 2 × 3 × 3 × 5 = 90
示例
Question: Find the LCM of 4, 8, and 16. Solution: Product of prime factors, 4 = 2 × 2 8 = 2 × 2 × 2 16 = 2 × 2 × 2 × 2 In all the given numbers, there is only one prime factor, i.e., 2. In 16, the prime factor 2 occurs for the maximum number of times, i.e., 4. So, the LCM of 4, 8, and 16 is, 2 × 2 × 2 × 2 = 16