
- TensorFlow 教程
- TensorFlow - 主頁
- TensorFlow - 介紹
- TensorFlow - 安裝
- 理解人工智慧
- 數學基礎
- 機器學習與深度學習
- TensorFlow - 基礎知識
- 卷積神經網路
- 迴圈神經網路
- TensorBoard 視覺化
- TensorFlow - 詞嵌入
- 單層感知器
- TensorFlow - 線性迴歸
- TFLearn 及其安裝
- CNN 和 RNN 的區別
- TensorFlow - Keras
- TensorFlow - 分散式計算
- TensorFlow - 匯出
- 多層感知器學習
- 感知器的隱藏層
- TensorFlow - 最佳化器
- TensorFlow - XOR 實現
- 梯度下降最佳化
- TensorFlow - 形成圖
- 使用 TensorFlow 進行影像識別
- 神經網路培訓建議
- TensorFlow 有用資源
- TensorFlow - 快速指南
- TensorFlow - 有用的資源
- TensorFlow - 討論
TensorFlow - XOR 實現
在本章中,我們將學習使用 TensorFlow 實現 XOR 的知識。在開始瞭解 TensorFlow 中的 XOR 實現之前,讓我們瞭解一下 XOR 表值。這將幫助我們瞭解加密和解密過程。
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XOR 密碼加密方法基本上用來加密很難用蠻力方法破解的資料,即生成匹配適當金鑰的隨機加密金鑰。
用 XOR 密碼實現的概念是定義一個 XOR 加密金鑰,然後用此金鑰對指定字串中的字元執行 XOR 運算,使用者試圖加密該字串。現在,我們將重點了解如何使用 TensorFlow 實現 XOR,方法如下 −
#Declaring necessary modules
import tensorflow as tf
import numpy as np
"""
A simple numpy implementation of a XOR gate to understand the backpropagation
algorithm
"""
x = tf.placeholder(tf.float64,shape = [4,2],name = "x")
#declaring a place holder for input x
y = tf.placeholder(tf.float64,shape = [4,1],name = "y")
#declaring a place holder for desired output y
m = np.shape(x)[0]#number of training examples
n = np.shape(x)[1]#number of features
hidden_s = 2 #number of nodes in the hidden layer
l_r = 1#learning rate initialization
theta1 = tf.cast(tf.Variable(tf.random_normal([3,hidden_s]),name = "theta1"),tf.float64)
theta2 = tf.cast(tf.Variable(tf.random_normal([hidden_s+1,1]),name = "theta2"),tf.float64)
#conducting forward propagation
a1 = tf.concat([np.c_[np.ones(x.shape[0])],x],1)
#the weights of the first layer are multiplied by the input of the first layer
z1 = tf.matmul(a1,theta1)
#the input of the second layer is the output of the first layer, passed through the
activation function and column of biases is added
a2 = tf.concat([np.c_[np.ones(x.shape[0])],tf.sigmoid(z1)],1)
#the input of the second layer is multiplied by the weights
z3 = tf.matmul(a2,theta2)
#the output is passed through the activation function to obtain the final probability
h3 = tf.sigmoid(z3)
cost_func = -tf.reduce_sum(y*tf.log(h3)+(1-y)*tf.log(1-h3),axis = 1)
#built in tensorflow optimizer that conducts gradient descent using specified
learning rate to obtain theta values
optimiser = tf.train.GradientDescentOptimizer(learning_rate = l_r).minimize(cost_func)
#setting required X and Y values to perform XOR operation
X = [[0,0],[0,1],[1,0],[1,1]]
Y = [[0],[1],[1],[0]]
#initializing all variables, creating a session and running a tensorflow session
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
#running gradient descent for each iteration and printing the hypothesis
obtained using the updated theta values
for i in range(100000):
sess.run(optimiser, feed_dict = {x:X,y:Y})#setting place holder values using feed_dict
if i%100==0:
print("Epoch:",i)
print("Hyp:",sess.run(h3,feed_dict = {x:X,y:Y}))
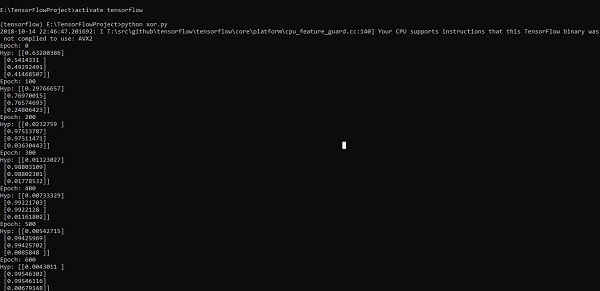
以上程式碼行生成的輸出如下圖所示 −
廣告