TensorFlow - 數學基礎

---

---

在 TensorFlow 中建立基本應用程式之前，瞭解 TensorFlow 所需的數學概念非常重要。數學被認為是任何機器學習演算法的核心。藉助數學的核心概念，可以定義特定機器學習演算法的解決方案。

向量

一個數字陣列，可以是連續的或離散的，被定義為向量。機器學習演算法處理固定長度的向量以獲得更好的輸出生成。

機器學習演算法處理多維資料，因此向量起著至關重要的作用。

向量模型的圖形表示如下所示：

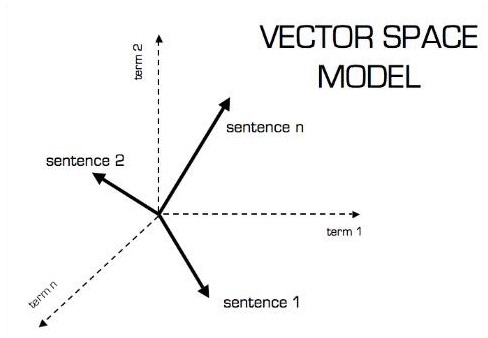
標量

標量可以定義為一維向量。標量是指僅包含大小而不包含方向的量。對於標量，我們只關注大小。

標量的示例包括兒童的體重和身高參數。

矩陣

矩陣可以定義為多維陣列，以行和列的形式排列。矩陣的大小由行長和列長定義。下圖顯示了任何指定矩陣的表示。

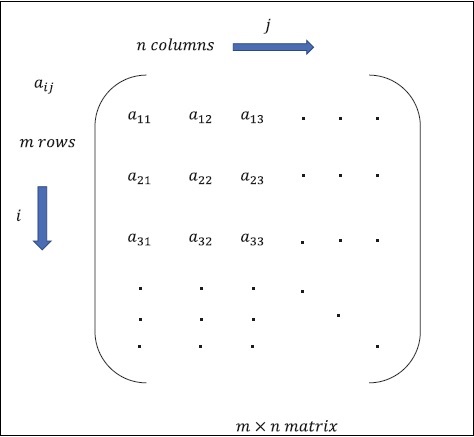
考慮上面提到的具有“m”行和“n”列的矩陣，矩陣表示將指定為“m*n 矩陣”，這也定義了矩陣的長度。

數學計算

在本節中，我們將學習 TensorFlow 中的不同數學計算。

矩陣加法

如果矩陣具有相同的維度，則可以對兩個或多個矩陣進行加法。加法意味著根據給定位置對每個元素進行加法。

考慮以下示例以瞭解矩陣加法的工作原理：

$$示例：A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B=\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}\:那麼\:A+B=\begin{bmatrix}1+5 & 2+6 \\3+7 & 4+8 \end{bmatrix}=\begin{bmatrix}6 & 8 \\10 & 12 \end{bmatrix}$$

矩陣減法

矩陣的減法操作方式類似於兩個矩陣的加法。使用者可以減去兩個矩陣，前提是維度相等。

$$示例：A-\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B-\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}\:那麼\:A-B-\begin{bmatrix}1-5 & 2-6 \\3-7 & 4-8 \end{bmatrix}-\begin{bmatrix}-4 & -4 \\-4 & -4 \end{bmatrix}$$

矩陣乘法

對於兩個矩陣 A m*n 和 B p*q 可乘，n 應該等於 p。生成的矩陣為：

C m*q

$$A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B=\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}$$

$$c_{11}=\begin{bmatrix}1 & 2 \end{bmatrix}\begin{bmatrix}5 \\7 \end{bmatrix}=1\times5+2\times7=19\:c_{12}=\begin{bmatrix}1 & 2 \end{bmatrix}\begin{bmatrix}6 \\8 \end{bmatrix}=1\times6+2\times8=22$$

$$c_{21}=\begin{bmatrix}3 & 4 \end{bmatrix}\begin{bmatrix}5 \\7 \end{bmatrix}=3\times5+4\times7=43\:c_{22}=\begin{bmatrix}3 & 4 \end{bmatrix}\begin{bmatrix}6 \\8 \end{bmatrix}=3\times6+4\times8=50$$

$$C=\begin{bmatrix}c_{11} & c_{12} \\c_{21} & c_{22} \end{bmatrix}=\begin{bmatrix}19 & 22 \\43 & 50 \end{bmatrix}$$

矩陣轉置

矩陣 A 的轉置，m*n 通常表示為 AT（轉置）n*m，透過將列向量轉置為行向量獲得。

$$示例：A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}\:那麼\:A^{T}\begin{bmatrix}1 & 3 \\2 & 4 \end{bmatrix}$$

向量的點積

任何維度為 n 的向量都可以表示為矩陣 v = R^n*1。

$$v_{1}=\begin{bmatrix}v_{11} \\v_{12} \\\cdot\\\cdot\\\cdot\\v_{1n}\end{bmatrix}v_{2}=\begin{bmatrix}v_{21} \\v_{22} \\\cdot\\\cdot\\\cdot\\v_{2n}\end{bmatrix}$$

兩個向量的點積是對應分量的乘積之和 - 沿相同維度的分量，可以表示為

$$v_{1}\cdot v_{2}=v_1^Tv_{2}=v_2^Tv_{1}=v_{11}v_{21}+v_{12}v_{22}+\cdot\cdot+v_{1n}v_{2n}=\displaystyle\sum\limits_{k=1}^n v_{1k}v_{2k}$$

下面提到了向量點積的示例：

$$示例：v_{1}=\begin{bmatrix}1 \\2 \\3\end{bmatrix}v_{2}=\begin{bmatrix}3 \\5 \\-1\end{bmatrix}v_{1}\cdot v_{2}=v_1^Tv_{2}=1\times3+2\times5-3\times1=10$$