TensorFlow - 線性迴歸

在本章中，我們將重點關注使用 TensorFlow 實現線性迴歸的基本示例。邏輯迴歸或線性迴歸是一種監督機器學習方法，用於對有序離散類別進行分類。我們本章的目標是構建一個模型，使用者可以透過該模型預測預測變數和一個或多個自變數之間的關係。

這兩個變數之間的關係被認為是線性的。如果 y 是因變數，x 被視為自變數，那麼這兩個變數的線性迴歸關係將如下式所示：

Y = Ax+b

我們將為線性迴歸設計一個演算法。這將使我們能夠理解以下兩個重要概念：

• 成本函式
• 梯度下降演算法

線性迴歸的示意圖如下所示：

線性迴歸方程的圖形檢視如下所示：

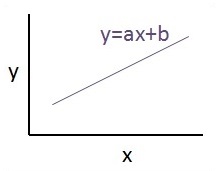
設計線性迴歸演算法的步驟

現在我們將學習有助於設計線性迴歸演算法的步驟。

步驟 1

匯入必要的模組以繪製線性迴歸模組非常重要。我們開始匯入 Python 庫 NumPy 和 Matplotlib。

import numpy as np 
import matplotlib.pyplot as plt

步驟 2

定義邏輯迴歸所需的係數數量。

number_of_points = 500 
x_point = [] 
y_point = [] 
a = 0.22 
b = 0.78

步驟 3

迭代變數以生成迴歸方程周圍的 300 個隨機點：

Y = 0.22x+0.78

for i in range(number_of_points): 
   x = np.random.normal(0.0,0.5) 
   y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) 
   y_point.append([y])

步驟 4

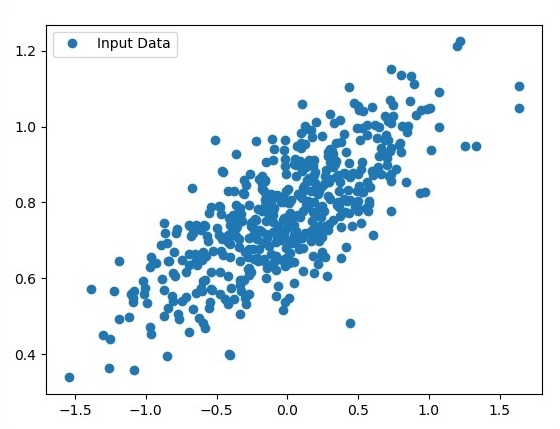
使用 Matplotlib 檢視生成的點。

fplt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() plt.show()

邏輯迴歸的完整程式碼如下：

import numpy as np 
import matplotlib.pyplot as plt 

number_of_points = 500 
x_point = [] 
y_point = [] 
a = 0.22 
b = 0.78 

for i in range(number_of_points): 
   x = np.random.normal(0.0,0.5) 
   y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) 
   y_point.append([y]) 
   
plt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() 
plt.show()

作為輸入獲取的點數被視為輸入資料。