- TensorFlow 教程
- TensorFlow - 首頁
- TensorFlow - 簡介
- TensorFlow - 安裝
- 理解人工智慧
- 數學基礎
- 機器學習與深度學習
- TensorFlow - 基礎
- 卷積神經網路
- 迴圈神經網路
- TensorBoard 視覺化
- TensorFlow - 詞嵌入
- 單層感知器
- TensorFlow - 線性迴歸
- TFLearn 及其安裝
- CNN 和 RNN 的區別
- TensorFlow - Keras
- TensorFlow - 分散式計算
- TensorFlow - 匯出
- 多層感知器學習
- 感知器的隱藏層
- TensorFlow - 最佳化器
- TensorFlow - XOR 實現
- 梯度下降最佳化
- TensorFlow - 構建圖
- 使用 TensorFlow 進行影像識別
- 神經網路訓練建議
- TensorFlow 有用資源
- TensorFlow 快速指南
- TensorFlow - 有用資源
- TensorFlow - 討論
TensorFlow 快速指南
TensorFlow - 簡介
TensorFlow 是一個軟體庫或框架,由 Google 團隊設計,以最簡單的方式實現機器學習和深度學習概念。它結合了最佳化技術的計算代數,可以輕鬆計算許多數學表示式。
TensorFlow 的官方網站如下所示:
現在讓我們考慮 TensorFlow 的以下重要特性:
它包含一個特性,可以藉助稱為張量的多維陣列輕鬆定義、最佳化和計算數學表示式。
它包含對深度神經網路和機器學習技術的程式設計支援。
它包含使用各種資料集進行計算的高可擴充套件性特性。
TensorFlow 使用 GPU 計算,並自動管理。它還包含一個獨特的特性,可以最佳化相同記憶體和使用的資料。
為什麼 TensorFlow 如此受歡迎?
TensorFlow 文件齊全,包含大量機器學習庫。它為此提供了一些重要的功能和方法。
TensorFlow 也被稱為“Google”產品。它包含各種機器學習和深度學習演算法。TensorFlow 可以訓練和執行深度神經網路,用於手寫數字分類、影像識別、詞嵌入以及建立各種序列模型。
TensorFlow - 安裝
要安裝 TensorFlow,系統中必須安裝“Python”。Python 3.4+ 版本被認為是開始安裝 TensorFlow 的最佳版本。
請考慮以下在 Windows 作業系統中安裝 TensorFlow 的步驟。
步驟 1 - 驗證已安裝的 python 版本。
步驟 2 - 使用者可以選擇任何機制在系統中安裝 TensorFlow。我們推薦“pip”和“Anaconda”。Pip 是一個用於在 Python 中執行和安裝模組的命令。
在安裝 TensorFlow 之前,我們需要在系統中安裝 Anaconda 框架。
安裝成功後,透過“conda”命令在命令提示符中進行檢查。命令執行如下所示:
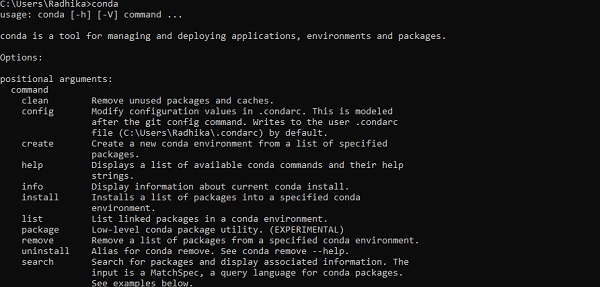
步驟 3 - 執行以下命令初始化 TensorFlow 的安裝:
conda create --name tensorflow python = 3.5
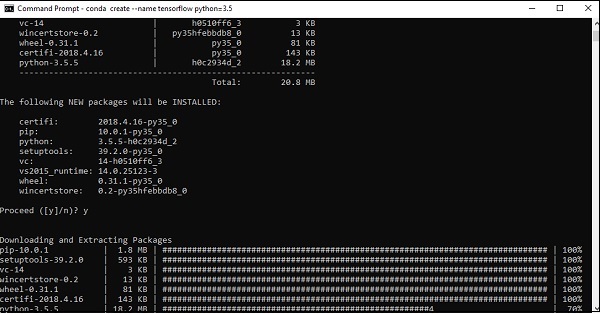
它會下載 TensorFlow 設定所需的必要軟體包。
步驟 4 - 環境設定成功後,務必啟用 TensorFlow 模組。
activate tensorflow
步驟 5 - 使用 pip 在系統中安裝“Tensorflow”。用於安裝的命令如下所示:
pip install tensorflow
並且,
pip install tensorflow-gpu
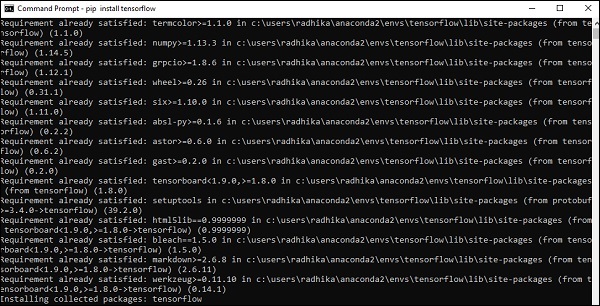
安裝成功後,瞭解 TensorFlow 的示例程式執行非常重要。
以下示例幫助我們理解 TensorFlow 中的基本程式建立“Hello World”。
第一個程式實現的程式碼如下所示:
>> activate tensorflow >> python (activating python shell) >> import tensorflow as tf >> hello = tf.constant(‘Hello, Tensorflow!’) >> sess = tf.Session() >> print(sess.run(hello))
理解人工智慧
人工智慧包括機器和特殊計算機系統模擬人類智慧的過程。人工智慧的例子包括學習、推理和自我糾正。AI 的應用包括語音識別、專家系統以及影像識別和機器視覺。
機器學習是人工智慧的一個分支,它處理可以學習任何新資料和資料模式的系統和演算法。
讓我們關注下面提到的韋恩圖,以理解機器學習和深度學習的概念。
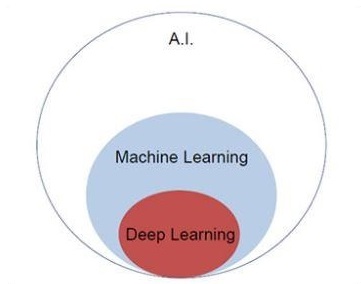
機器學習包含機器學習的一部分,深度學習是機器學習的一部分。遵循機器學習概念的程式的能力是提高其觀察資料的效能。資料轉換的主要動機是提高其知識,以便在未來獲得更好的結果,為該特定系統提供更接近所需輸出的輸出。機器學習包括“模式識別”,其中包括識別資料中模式的能力。
應訓練這些模式以以理想的方式顯示輸出。
機器學習可以透過兩種不同的方式進行訓練:
- 監督訓練
- 無監督訓練
監督學習
監督學習或監督訓練包括一個過程,其中訓練集作為輸入提供給系統,其中每個示例都用所需的輸出值進行標記。此型別的訓練是使用最小化特定損失函式來執行的,該函式表示相對於所需輸出系統的輸出誤差。
訓練完成後,根據與訓練集分離的示例(也稱為驗證集)衡量每個模型的準確性。
說明“監督學習”的最佳示例是一堆帶有包含在其中的資訊的圖片。在這裡,使用者可以訓練模型來識別新的圖片。
無監督學習
在無監督學習或無監督訓練中,包括訓練示例,這些示例未被系統標記為屬於哪個類別。系統查詢共享共同特徵的資料,並根據內部知識特徵更改它們。這種型別的學習演算法主要用於聚類問題。
說明“無監督學習”的最佳示例是一堆沒有包含資訊的圖片,使用者使用分類和聚類訓練模型。這種型別的訓練演算法在沒有提供資訊的情況下進行假設。
TensorFlow - 數學基礎
在建立 TensorFlow 中的基本應用程式之前,瞭解 TensorFlow 所需的數學概念非常重要。數學被認為是任何機器學習演算法的核心。藉助數學的核心概念,可以定義特定機器學習演算法的解決方案。
向量
定義為連續或離散的數字陣列。機器學習演算法處理固定長度的向量以生成更好的輸出。
機器學習演算法處理多維資料,因此向量起著至關重要的作用。

向量模型的圖形表示如下所示:
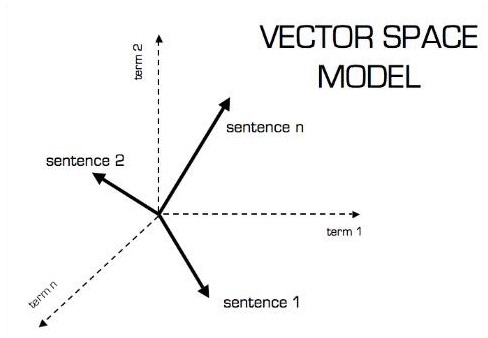
標量
標量可以定義為一維向量。標量是那些僅包含大小而不包含方向的標量。對於標量,我們只關心大小。
標量的示例包括兒童的體重和身高參數。
矩陣
矩陣可以定義為多維陣列,以行和列的形式排列。矩陣的大小由行長度和列長度定義。下圖顯示了任何指定矩陣的表示。
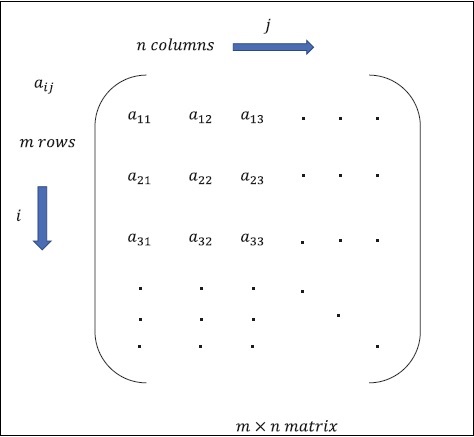
考慮上面提到的具有“m”行和“n”列的矩陣,矩陣表示將指定為“m*n 矩陣”,這也定義了矩陣的長度。
數學計算
在本節中,我們將學習 TensorFlow 中的不同數學計算。
矩陣加法
如果矩陣具有相同的維度,則可以對兩個或多個矩陣進行加法。加法意味著根據給定位置對每個元素進行加法。
請考慮以下示例以瞭解矩陣加法的工作原理:
$$示例:A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B=\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}\:那麼\:A+B=\begin{bmatrix}1+5 & 2+6 \\3+7 & 4+8 \end{bmatrix}=\begin{bmatrix}6 & 8 \\10 & 12 \end{bmatrix}$$
矩陣減法
矩陣減法與兩個矩陣的加法類似。使用者可以減去兩個矩陣,前提是維度相等。
$$示例:A-\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B-\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}\:那麼\:A-B-\begin{bmatrix}1-5 & 2-6 \\3-7 & 4-8 \end{bmatrix}-\begin{bmatrix}-4 & -4 \\-4 & -4 \end{bmatrix}$$
矩陣乘法
對於兩個矩陣 A m*n 和 B p*q 可以相乘,n 應等於 p。生成的矩陣為:
C m*q
$$A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B=\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}$$
$$c_{11}=\begin{bmatrix}1 & 2 \end{bmatrix}\begin{bmatrix}5 \\7 \end{bmatrix}=1\times5+2\times7=19\:c_{12}=\begin{bmatrix}1 & 2 \end{bmatrix}\begin{bmatrix}6 \\8 \end{bmatrix}=1\times6+2\times8=22$$
$$c_{21}=\begin{bmatrix}3 & 4 \end{bmatrix}\begin{bmatrix}5 \\7 \end{bmatrix}=3\times5+4\times7=43\:c_{22}=\begin{bmatrix}3 & 4 \end{bmatrix}\begin{bmatrix}6 \\8 \end{bmatrix}=3\times6+4\times8=50$$
$$C=\begin{bmatrix}c_{11} & c_{12} \\c_{21} & c_{22} \end{bmatrix}=\begin{bmatrix}19 & 22 \\43 & 50 \end{bmatrix}$$
矩陣轉置
矩陣 A 的轉置,m*n 通常用 AT(轉置)n*m 表示,它是透過將列向量轉置為行向量獲得的。
$$示例:A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}\:那麼\:A^{T}\begin{bmatrix}1 & 3 \\2 & 4 \end{bmatrix}$$
向量的點積
任何維度為 n 的向量都可以表示為矩陣 v = R^n*1。
$$v_{1}=\begin{bmatrix}v_{11} \\v_{12} \\\cdot\\\cdot\\\cdot\\v_{1n}\end{bmatrix}v_{2}=\begin{bmatrix}v_{21} \\v_{22} \\\cdot\\\cdot\\\cdot\\v_{2n}\end{bmatrix}$$
兩個向量的點積是對應分量的乘積之和 - 沿相同維度的分量,可以表示為
$$v_{1}\cdot v_{2}=v_1^Tv_{2}=v_2^Tv_{1}=v_{11}v_{21}+v_{12}v_{22}+\cdot\cdot+v_{1n}v_{2n}=\displaystyle\sum\limits_{k=1}^n v_{1k}v_{2k}$$
向量的點積示例如下所示:
$$示例:v_{1}=\begin{bmatrix}1 \\2 \\3\end{bmatrix}v_{2}=\begin{bmatrix}3 \\5 \\-1\end{bmatrix}v_{1}\cdot v_{2}=v_1^Tv_{2}=1\times3+2\times5-3\times1=10$$
機器學習和深度學習
人工智慧是近些年來最流行的趨勢之一。機器學習和深度學習構成了人工智慧。下面所示的韋恩圖解釋了機器學習和深度學習的關係:

機器學習
機器學習是讓計算機根據設計的演算法和程式進行操作的科學藝術。許多研究人員認為機器學習是朝著人類水平人工智慧取得進展的最佳途徑。機器學習包括以下型別的模式
- 監督學習模式
- 無監督學習模式
深度學習
深度學習是機器學習的一個子領域,其中相關的演算法受到稱為人工神經網路的大腦結構和功能的啟發。
深度學習今天所有的價值都是透過監督學習或從標記資料和演算法中學習獲得的。
深度學習中的每個演算法都經歷相同的過程。它包括輸入的非線性變換的層次結構,可用於生成作為輸出的統計模型。
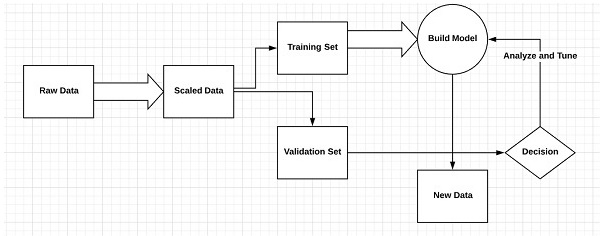
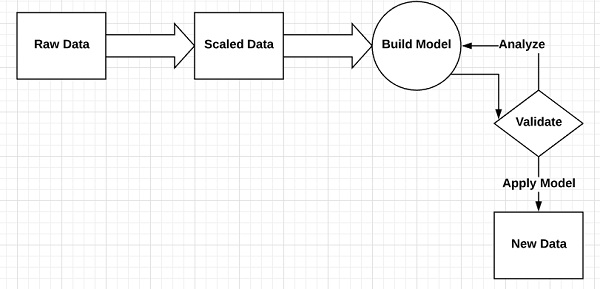
考慮定義機器學習過程的以下步驟
- 識別相關資料集並準備它們進行分析。
- 選擇要使用的演算法型別
- 基於所使用的演算法構建分析模型。
- 在測試資料集上訓練模型,並在需要時進行修改。
- 執行模型以生成測試分數。
機器學習和深度學習的區別
在本節中,我們將瞭解機器學習和深度學習之間的區別。
資料量
機器學習使用大量資料。它也適用於少量資料。另一方面,深度學習如果資料量迅速增加,則可以高效地工作。下圖顯示了機器學習和深度學習隨資料量變化的工作方式 -
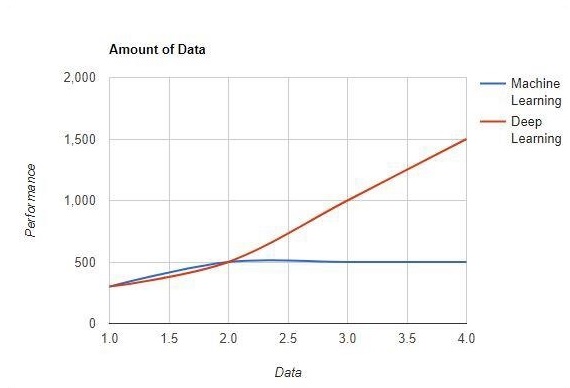
硬體依賴性
與傳統的機器學習演算法不同,深度學習演算法被設計為嚴重依賴於高階機器。深度學習演算法執行大量矩陣乘法運算,這需要大量的硬體支援。
特徵工程
特徵工程是將領域知識放入指定特徵中以降低資料複雜度並使學習演算法可見的模式的過程。
例如 - 傳統的機器學習模式側重於畫素和其他特徵工程過程所需的屬性。深度學習演算法專注於資料中的高階特徵。它減少了為每個新問題開發新的特徵提取器的任務。
問題解決方法
傳統的機器學習演算法遵循標準程式來解決問題。它將問題分解成多個部分,解決每個部分,並將它們組合起來以獲得所需的結果。深度學習專注於端到端地解決問題,而不是將其分解成多個部分。
執行時間
執行時間是訓練演算法所需的時間。深度學習需要大量時間來訓練,因為它包含大量引數,這比平時需要更長的時間。機器學習演算法相對需要較少的執行時間。
可解釋性
可解釋性是比較機器學習和深度學習演算法的主要因素。主要原因是深度學習在工業應用之前仍然需要謹慎考慮。
機器學習和深度學習的應用
在本節中,我們將學習機器學習和深度學習的不同應用。
計算機視覺,用於人臉識別和透過指紋或車牌識別車輛進行考勤標記。
從搜尋引擎中檢索資訊,例如文字搜尋以進行影像搜尋。
自動電子郵件營銷,並指定目標識別。
癌症腫瘤的醫學診斷或任何慢性疾病的異常識別。
自然語言處理,用於照片標記等應用。解釋這種情況的最佳示例是在 Facebook 中使用。
線上廣告。
未來趨勢
隨著資料科學和機器學習在行業中使用的趨勢不斷增強,每個組織將機器學習融入其業務變得越來越重要。
深度學習正變得比機器學習更重要。深度學習被證明是最新效能的最佳技術之一。
機器學習和深度學習將證明對研究和學術領域有益。
結論
在本文中,我們概述了機器學習和深度學習,並配以插圖和差異,也重點關注了未來趨勢。許多 AI 應用主要利用機器學習演算法來推動自助服務、提高座席工作效率以及使工作流程更可靠。機器學習和深度學習演算法為許多企業和行業領導者帶來了令人興奮的前景。
TensorFlow - 基礎
在本章中,我們將學習 TensorFlow 的基礎知識。我們將從瞭解張量的 資料結構開始。
張量資料結構
張量在 TensorFlow 語言中用作基本資料結構。張量表示任何稱為資料流圖的流程圖中的連線邊。張量被定義為多維陣列或列表。
張量由以下三個引數標識 -
秩
張量中描述的維度單位稱為秩。它標識張量的維度數。張量的秩可以描述為張量定義的階數或 n 維。
形狀
行數和列數一起定義張量的形狀。
型別
型別描述分配給張量元素的資料型別。
使用者需要考慮以下活動來構建張量 -
- 構建一個 n 維陣列
- 轉換 n 維陣列。
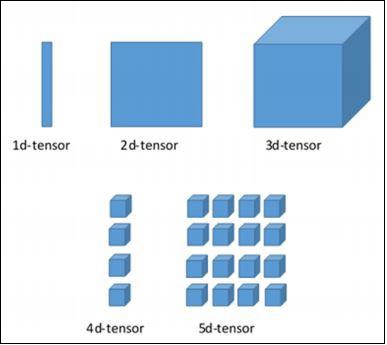
TensorFlow 的各個維度
TensorFlow 包括各種維度。下面簡要描述了這些維度 -
一維張量
一維張量是一種普通的陣列結構,它包含一組相同資料型別的值。
宣告
>>> import numpy as np >>> tensor_1d = np.array([1.3, 1, 4.0, 23.99]) >>> print tensor_1d
下面螢幕截圖中顯示了帶有輸出的實現 -
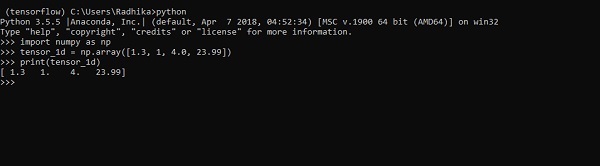
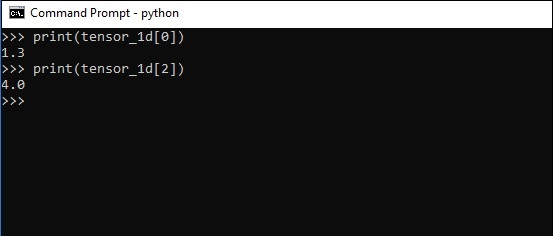
元素的索引與 Python 列表相同。第一個元素的索引從 0 開始;要透過索引列印值,您只需提及索引號。
>>> print tensor_1d[0] 1.3 >>> print tensor_1d[2] 4.0
二維張量
一系列陣列用於建立“二維張量”。
下面描述了二維張量的建立 -
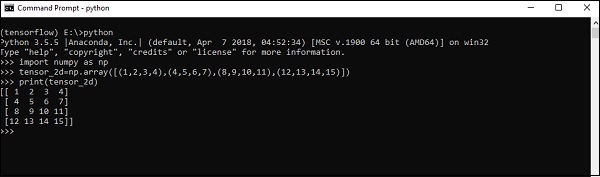
以下是建立二維陣列的完整語法 -
>>> import numpy as np >>> tensor_2d = np.array([(1,2,3,4),(4,5,6,7),(8,9,10,11),(12,13,14,15)]) >>> print(tensor_2d) [[ 1 2 3 4] [ 4 5 6 7] [ 8 9 10 11] [12 13 14 15]] >>>
可以透過指定為索引號的行號和列號來跟蹤二維張量的特定元素。
>>> tensor_2d[3][2] 14
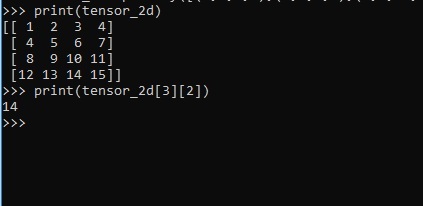
張量處理和操作
在本節中,我們將學習張量處理和操作。
首先,讓我們考慮以下程式碼 -
import tensorflow as tf import numpy as np matrix1 = np.array([(2,2,2),(2,2,2),(2,2,2)],dtype = 'int32') matrix2 = np.array([(1,1,1),(1,1,1),(1,1,1)],dtype = 'int32') print (matrix1) print (matrix2) matrix1 = tf.constant(matrix1) matrix2 = tf.constant(matrix2) matrix_product = tf.matmul(matrix1, matrix2) matrix_sum = tf.add(matrix1,matrix2) matrix_3 = np.array([(2,7,2),(1,4,2),(9,0,2)],dtype = 'float32') print (matrix_3) matrix_det = tf.matrix_determinant(matrix_3) with tf.Session() as sess: result1 = sess.run(matrix_product) result2 = sess.run(matrix_sum) result3 = sess.run(matrix_det) print (result1) print (result2) print (result3)
輸出
以上程式碼將生成以下輸出 -
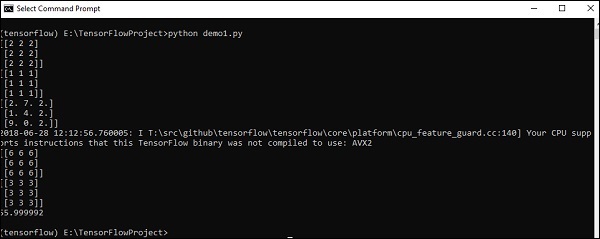
解釋
我們在上面的原始碼中建立了多維陣列。現在,重要的是要理解我們建立了圖和會話,它們管理張量並生成相應的輸出。藉助圖,我們獲得了指定張量之間數學計算的輸出。
TensorFlow - 卷積神經網路
在理解機器學習概念之後,我們現在可以將注意力轉移到深度學習概念上。深度學習是機器學習的一個分支,被認為是近幾十年來研究人員採取的關鍵步驟。深度學習實現的示例包括影像識別和語音識別等應用。
以下是兩種重要的深度神經網路型別 -
- 卷積神經網路
- 迴圈神經網路
在本章中,我們將重點關注 CNN,即卷積神經網路。
卷積神經網路
卷積神經網路旨在透過多層陣列處理資料。這種型別的神經網路用於影像識別或人臉識別等應用。CNN 與任何其他普通神經網路的主要區別在於,CNN 將輸入作為二維陣列,並直接對影像進行操作,而不是專注於其他神經網路所關注的特徵提取。
CNN 的主要方法包括解決識別問題的方案。谷歌和 Facebook 等頂級公司已投資於識別專案的研發,以更快地完成活動。
卷積神經網路使用三個基本思想 -
- 區域性感受野
- 卷積
- 池化
讓我們詳細瞭解這些想法。
CNN 利用輸入資料中存在的空間相關性。神經網路的每個併發層都連線一些輸入神經元。這個特定區域稱為區域性感受野。區域性感受野側重於隱藏神經元。隱藏神經元處理上述欄位內的輸入資料,而沒有意識到特定邊界之外的變化。
以下是生成區域性感受野的圖表表示 -
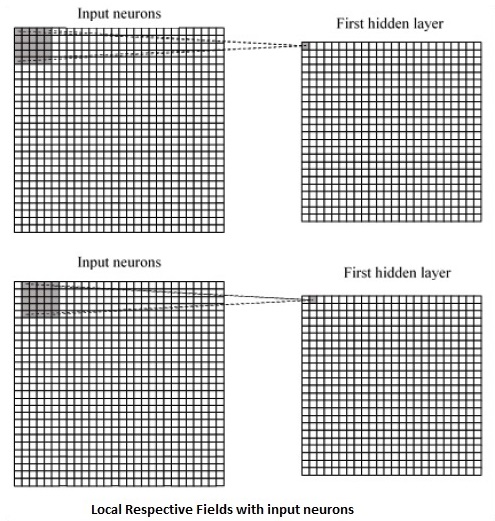
如果我們觀察上述表示,每個連線都會學習隱藏神經元與從一層到另一層移動的相關連線的權重。在這裡,單個神經元會不時地發生偏移。此過程稱為“卷積”。
從輸入層到隱藏特徵圖的連線對映被定義為“共享權重”,包含的偏差稱為“共享偏差”。
CNN 或卷積神經網路使用池化層,這些層是 CNN 聲明後立即放置的層。它將使用者的輸入作為來自卷積網路的特徵圖,並準備一個濃縮的特徵圖。池化層有助於建立具有前一層神經元的層。
CNN 的 TensorFlow 實現
在本節中,我們將學習 CNN 的 TensorFlow 實現。執行整個網路並使其具有適當維度所需的步驟如下所示 -
步驟 1 - 包括 TensorFlow 和資料集模組所需的模組,這些模組是計算 CNN 模型所必需的。
import tensorflow as tf import numpy as np from tensorflow.examples.tutorials.mnist import input_data
步驟 2 - 宣告一個名為 run_cnn() 的函式,該函式包含各種引數和最佳化變數以及資料佔位符的宣告。這些最佳化變數將宣告訓練模式。
def run_cnn():
mnist = input_data.read_data_sets("MNIST_data/", one_hot = True)
learning_rate = 0.0001
epochs = 10
batch_size = 50
步驟 3 - 在此步驟中,我們將使用輸入引數宣告訓練資料佔位符 - 對於 28 x 28 畫素 = 784。這是從 mnist.train.nextbatch() 中提取的扁平化影像資料。
我們可以根據需要重新整形張量。第一個值 (-1) 告訴函式根據傳遞給它的資料量動態地整形該維度。兩個中間維度設定為影像大小(即 28 x 28)。
x = tf.placeholder(tf.float32, [None, 784]) x_shaped = tf.reshape(x, [-1, 28, 28, 1]) y = tf.placeholder(tf.float32, [None, 10])
步驟 4 - 現在,重要的是建立一些卷積層 -
layer1 = create_new_conv_layer(x_shaped, 1, 32, [5, 5], [2, 2], name = 'layer1') layer2 = create_new_conv_layer(layer1, 32, 64, [5, 5], [2, 2], name = 'layer2')
步驟 5 - 讓我們將輸出展平以準備好用於全連線輸出階段 - 在兩層步長為 2 的池化之後,維度為 28 x 28,到維度為 14 x 14 或最小 7 x 7 x,y 座標,但有 64 個輸出通道。要使用“密集”層建立全連線,新形狀需要為 [-1, 7 x 7 x 64]。我們可以為此層設定一些權重和偏差值,然後使用 ReLU 啟用。
flattened = tf.reshape(layer2, [-1, 7 * 7 * 64]) wd1 = tf.Variable(tf.truncated_normal([7 * 7 * 64, 1000], stddev = 0.03), name = 'wd1') bd1 = tf.Variable(tf.truncated_normal([1000], stddev = 0.01), name = 'bd1') dense_layer1 = tf.matmul(flattened, wd1) + bd1 dense_layer1 = tf.nn.relu(dense_layer1)
步驟 6 - 另一個具有特定 softmax 啟用的層以及所需的最佳化器定義了準確性評估,這使得初始化運算子的設定成為可能。
wd2 = tf.Variable(tf.truncated_normal([1000, 10], stddev = 0.03), name = 'wd2') bd2 = tf.Variable(tf.truncated_normal([10], stddev = 0.01), name = 'bd2') dense_layer2 = tf.matmul(dense_layer1, wd2) + bd2 y_ = tf.nn.softmax(dense_layer2) cross_entropy = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits(logits = dense_layer2, labels = y)) optimiser = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cross_entropy) correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) init_op = tf.global_variables_initializer()
步驟 7 - 我們應該設定記錄變數。這增加了一個摘要來儲存資料的準確性。
tf.summary.scalar('accuracy', accuracy)
merged = tf.summary.merge_all()
writer = tf.summary.FileWriter('E:\TensorFlowProject')
with tf.Session() as sess:
sess.run(init_op)
total_batch = int(len(mnist.train.labels) / batch_size)
for epoch in range(epochs):
avg_cost = 0
for i in range(total_batch):
batch_x, batch_y = mnist.train.next_batch(batch_size = batch_size)
_, c = sess.run([optimiser, cross_entropy], feed_dict = {
x:batch_x, y: batch_y})
avg_cost += c / total_batch
test_acc = sess.run(accuracy, feed_dict = {x: mnist.test.images, y:
mnist.test.labels})
summary = sess.run(merged, feed_dict = {x: mnist.test.images, y:
mnist.test.labels})
writer.add_summary(summary, epoch)
print("\nTraining complete!")
writer.add_graph(sess.graph)
print(sess.run(accuracy, feed_dict = {x: mnist.test.images, y:
mnist.test.labels}))
def create_new_conv_layer(
input_data, num_input_channels, num_filters,filter_shape, pool_shape, name):
conv_filt_shape = [
filter_shape[0], filter_shape[1], num_input_channels, num_filters]
weights = tf.Variable(
tf.truncated_normal(conv_filt_shape, stddev = 0.03), name = name+'_W')
bias = tf.Variable(tf.truncated_normal([num_filters]), name = name+'_b')
#Out layer defines the output
out_layer =
tf.nn.conv2d(input_data, weights, [1, 1, 1, 1], padding = 'SAME')
out_layer += bias
out_layer = tf.nn.relu(out_layer)
ksize = [1, pool_shape[0], pool_shape[1], 1]
strides = [1, 2, 2, 1]
out_layer = tf.nn.max_pool(
out_layer, ksize = ksize, strides = strides, padding = 'SAME')
return out_layer
if __name__ == "__main__":
run_cnn()
以下是上述程式碼生成的輸出 -
See @{tf.nn.softmax_cross_entropy_with_logits_v2}.
2018-09-19 17:22:58.802268: I
T:\src\github\tensorflow\tensorflow\core\platform\cpu_feature_guard.cc:140]
Your CPU supports instructions that this TensorFlow binary was not compiled to
use: AVX2
2018-09-19 17:25:41.522845: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 1003520000 exceeds 10% of system memory.
2018-09-19 17:25:44.630941: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 501760000 exceeds 10% of system memory.
Epoch: 1 cost = 0.676 test accuracy: 0.940
2018-09-19 17:26:51.987554: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 1003520000 exceeds 10% of system memory.
TensorFlow - 迴圈神經網路
迴圈神經網路是一種面向深度學習的演算法,它遵循順序方法。在神經網路中,我們總是假設每個輸入和輸出都獨立於所有其他層。這類神經網路被稱為迴圈神經網路,因為它們以順序方式執行數學計算。
考慮以下訓練迴圈神經網路的步驟:
步驟 1 - 從資料集中輸入一個特定示例。
步驟 2 - 網路將獲取一個示例,並使用隨機初始化的變數進行一些計算。
步驟 3 - 然後計算預測結果。
步驟 4 - 生成的實際結果與期望值的比較將產生誤差。
步驟 5 - 為了跟蹤誤差,它會透過相同的路徑傳播,其中變數也會被調整。
步驟 6 - 重複步驟 1 到 5,直到我們確信宣告以獲取輸出的變數已正確定義。
步驟 7 - 透過應用這些變數來獲取新的未見輸入,從而進行系統預測。
下面描述了表示迴圈神經網路的示意圖方法:
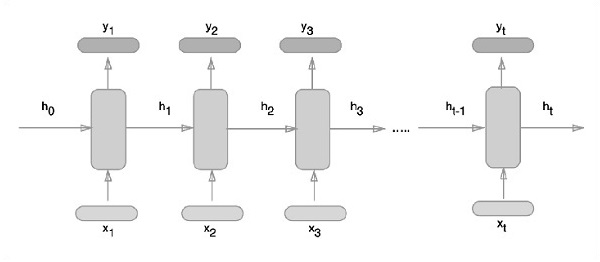
使用 TensorFlow 實現迴圈神經網路
在本節中,我們將學習如何使用 TensorFlow 實現迴圈神經網路。
步驟 1 - TensorFlow 包含用於迴圈神經網路模組的特定實現的各種庫。
#Import necessary modules
from __future__ import print_function
import tensorflow as tf
from tensorflow.contrib import rnn
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)
如上所述,這些庫有助於定義輸入資料,這是迴圈神經網路實現的主要部分。
步驟 2 - 我們的主要目的是使用迴圈神經網路對影像進行分類,其中我們將每張影像的行視為畫素序列。MNIST 影像形狀被特別定義為 28*28 px。現在我們將處理每個樣本提到的 28 個序列的 28 個步驟。我們將定義輸入引數以完成順序模式。
n_input = 28 # MNIST data input with img shape 28*28
n_steps = 28
n_hidden = 128
n_classes = 10
# tf Graph input
x = tf.placeholder("float", [None, n_steps, n_input])
y = tf.placeholder("float", [None, n_classes]
weights = {
'out': tf.Variable(tf.random_normal([n_hidden, n_classes]))
}
biases = {
'out': tf.Variable(tf.random_normal([n_classes]))
}
步驟 3 - 使用 RNN 中定義的函式計算結果以獲得最佳結果。在這裡,每個資料形狀都與當前輸入形狀進行比較,並計算結果以保持準確率。
def RNN(x, weights, biases): x = tf.unstack(x, n_steps, 1) # Define a lstm cell with tensorflow lstm_cell = rnn.BasicLSTMCell(n_hidden, forget_bias=1.0) # Get lstm cell output outputs, states = rnn.static_rnn(lstm_cell, x, dtype = tf.float32) # Linear activation, using rnn inner loop last output return tf.matmul(outputs[-1], weights['out']) + biases['out'] pred = RNN(x, weights, biases) # Define loss and optimizer cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = pred, labels = y)) optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost) # Evaluate model correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1)) accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32)) # Initializing the variables init = tf.global_variables_initializer()
步驟 4 - 在此步驟中,我們將啟動圖形以獲取計算結果。這也有助於計算測試結果的準確性。
with tf.Session() as sess:
sess.run(init)
step = 1
# Keep training until reach max iterations
while step * batch_size < training_iters:
batch_x, batch_y = mnist.train.next_batch(batch_size)
batch_x = batch_x.reshape((batch_size, n_steps, n_input))
sess.run(optimizer, feed_dict={x: batch_x, y: batch_y})
if step % display_step == 0:
# Calculate batch accuracy
acc = sess.run(accuracy, feed_dict={x: batch_x, y: batch_y})
# Calculate batch loss
loss = sess.run(cost, feed_dict={x: batch_x, y: batch_y})
print("Iter " + str(step*batch_size) + ", Minibatch Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
step += 1
print("Optimization Finished!")
test_len = 128
test_data = mnist.test.images[:test_len].reshape((-1, n_steps, n_input))
test_label = mnist.test.labels[:test_len]
print("Testing Accuracy:", \
sess.run(accuracy, feed_dict={x: test_data, y: test_label}))
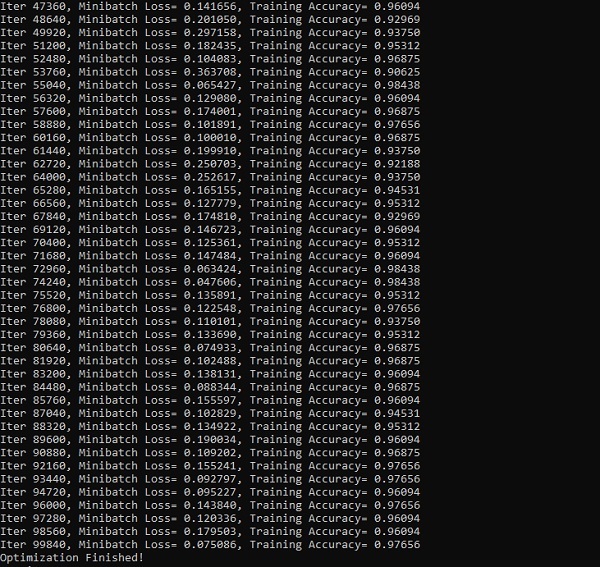
以下螢幕截圖顯示了生成的輸出:
TensorFlow - TensorBoard 視覺化
TensorFlow 包含一個視覺化工具,稱為 TensorBoard。它用於分析資料流圖,也用於理解機器學習模型。TensorBoard 的重要功能包括檢視關於引數的不同型別的統計資訊以及任何圖形的垂直對齊細節。
深度神經網路包含多達 36,000 個節點。TensorBoard 有助於將這些節點摺疊到高階塊中並突出顯示相同的結構。這允許更好地分析圖形,重點關注計算圖的主要部分。TensorBoard 視覺化被認為是非常互動式的,使用者可以平移、縮放和展開節點以顯示詳細資訊。
以下示意圖表示顯示了 TensorBoard 視覺化的完整工作原理:
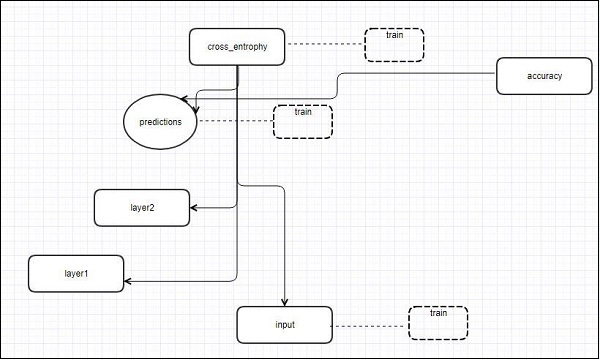
這些演算法將節點摺疊成高階塊,並突出顯示具有相同結構的特定組,這些組將高階節點分開。因此建立的 TensorBoard 很有用,並且被視為調整機器學習模型同等重要。此視覺化工具專為包含摘要資訊和需要顯示的詳細資訊的配置日誌檔案而設計。
讓我們藉助以下程式碼重點關注 TensorBoard 視覺化的演示示例:
import tensorflow as tf
# Constants creation for TensorBoard visualization
a = tf.constant(10,name = "a")
b = tf.constant(90,name = "b")
y = tf.Variable(a+b*2,name = 'y')
model = tf.initialize_all_variables() #Creation of model
with tf.Session() as session:
merged = tf.merge_all_summaries()
writer = tf.train.SummaryWriter("/tmp/tensorflowlogs",session.graph)
session.run(model)
print(session.run(y))
下表顯示了用於節點表示的 TensorBoard 視覺化的各種符號:

TensorFlow - 詞嵌入
詞嵌入是將離散物件(如單詞)對映到向量和實數的概念。它對於機器學習的輸入很重要。該概念包括標準函式,這些函式可以有效地將離散輸入物件轉換為有用的向量。
詞嵌入輸入的示例圖如下所示:
blue: (0.01359, 0.00075997, 0.24608, ..., -0.2524, 1.0048, 0.06259) blues: (0.01396, 0.11887, -0.48963, ..., 0.033483, -0.10007, 0.1158) orange: (-0.24776, -0.12359, 0.20986, ..., 0.079717, 0.23865, -0.014213) oranges: (-0.35609, 0.21854, 0.080944, ..., -0.35413, 0.38511, -0.070976)
Word2vec
Word2vec 是用於無監督詞嵌入技術的最常用方法。它以這樣一種方式訓練模型:給定一個輸入詞,透過使用跳躍語法來預測該詞的上下文。
TensorFlow 提供了許多方法來實現這種模型,這些方法具有越來越高的複雜性和最佳化水平,並使用多執行緒概念和更高級別的抽象。
import os
import math
import numpy as np
import tensorflow as tf
from tensorflow.contrib.tensorboard.plugins import projector
batch_size = 64
embedding_dimension = 5
negative_samples = 8
LOG_DIR = "logs/word2vec_intro"
digit_to_word_map = {
1: "One",
2: "Two",
3: "Three",
4: "Four",
5: "Five",
6: "Six",
7: "Seven",
8: "Eight",
9: "Nine"}
sentences = []
# Create two kinds of sentences - sequences of odd and even digits.
for i in range(10000):
rand_odd_ints = np.random.choice(range(1, 10, 2), 3)
sentences.append(" ".join([digit_to_word_map[r] for r in rand_odd_ints]))
rand_even_ints = np.random.choice(range(2, 10, 2), 3)
sentences.append(" ".join([digit_to_word_map[r] for r in rand_even_ints]))
# Map words to indices
word2index_map = {}
index = 0
for sent in sentences:
for word in sent.lower().split():
if word not in word2index_map:
word2index_map[word] = index
index += 1
index2word_map = {index: word for word, index in word2index_map.items()}
vocabulary_size = len(index2word_map)
# Generate skip-gram pairs
skip_gram_pairs = []
for sent in sentences:
tokenized_sent = sent.lower().split()
for i in range(1, len(tokenized_sent)-1):
word_context_pair = [[word2index_map[tokenized_sent[i-1]],
word2index_map[tokenized_sent[i+1]]], word2index_map[tokenized_sent[i]]]
skip_gram_pairs.append([word_context_pair[1], word_context_pair[0][0]])
skip_gram_pairs.append([word_context_pair[1], word_context_pair[0][1]])
def get_skipgram_batch(batch_size):
instance_indices = list(range(len(skip_gram_pairs)))
np.random.shuffle(instance_indices)
batch = instance_indices[:batch_size]
x = [skip_gram_pairs[i][0] for i in batch]
y = [[skip_gram_pairs[i][1]] for i in batch]
return x, y
# batch example
x_batch, y_batch = get_skipgram_batch(8)
x_batch
y_batch
[index2word_map[word] for word in x_batch] [index2word_map[word[0]] for word in y_batch]
# Input data, labels train_inputs = tf.placeholder(tf.int32, shape = [batch_size])
train_labels = tf.placeholder(tf.int32, shape = [batch_size, 1])
# Embedding lookup table currently only implemented in CPU with
tf.name_scope("embeddings"):
embeddings = tf.Variable(
tf.random_uniform([vocabulary_size, embedding_dimension], -1.0, 1.0),
name = 'embedding')
# This is essentialy a lookup table
embed = tf.nn.embedding_lookup(embeddings, train_inputs)
# Create variables for the NCE loss
nce_weights = tf.Variable(
tf.truncated_normal([vocabulary_size, embedding_dimension], stddev = 1.0 /
math.sqrt(embedding_dimension)))
nce_biases = tf.Variable(tf.zeros([vocabulary_size]))
loss = tf.reduce_mean(
tf.nn.nce_loss(weights = nce_weights, biases = nce_biases, inputs = embed,
labels = train_labels,num_sampled = negative_samples,
num_classes = vocabulary_size)) tf.summary.scalar("NCE_loss", loss)
# Learning rate decay
global_step = tf.Variable(0, trainable = False)
learningRate = tf.train.exponential_decay(learning_rate = 0.1,
global_step = global_step, decay_steps = 1000, decay_rate = 0.95, staircase = True)
train_step = tf.train.GradientDescentOptimizer(learningRate).minimize(loss)
merged = tf.summary.merge_all()
with tf.Session() as sess:
train_writer = tf.summary.FileWriter(LOG_DIR,
graph = tf.get_default_graph())
saver = tf.train.Saver()
with open(os.path.join(LOG_DIR, 'metadata.tsv'), "w") as metadata:
metadata.write('Name\tClass\n') for k, v in index2word_map.items():
metadata.write('%s\t%d\n' % (v, k))
config = projector.ProjectorConfig()
embedding = config.embeddings.add() embedding.tensor_name = embeddings.name
# Link this tensor to its metadata file (e.g. labels).
embedding.metadata_path = os.path.join(LOG_DIR, 'metadata.tsv')
projector.visualize_embeddings(train_writer, config)
tf.global_variables_initializer().run()
for step in range(1000):
x_batch, y_batch = get_skipgram_batch(batch_size) summary, _ = sess.run(
[merged, train_step], feed_dict = {train_inputs: x_batch, train_labels: y_batch})
train_writer.add_summary(summary, step)
if step % 100 == 0:
saver.save(sess, os.path.join(LOG_DIR, "w2v_model.ckpt"), step)
loss_value = sess.run(loss, feed_dict = {
train_inputs: x_batch, train_labels: y_batch})
print("Loss at %d: %.5f" % (step, loss_value))
# Normalize embeddings before using
norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims = True))
normalized_embeddings = embeddings /
norm normalized_embeddings_matrix = sess.run(normalized_embeddings)
ref_word = normalized_embeddings_matrix[word2index_map["one"]]
cosine_dists = np.dot(normalized_embeddings_matrix, ref_word)
ff = np.argsort(cosine_dists)[::-1][1:10] for f in ff: print(index2word_map[f])
print(cosine_dists[f])
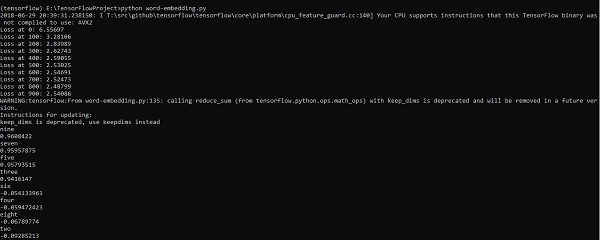
輸出
以上程式碼生成以下輸出:
TensorFlow - 單層感知器
為了理解單層感知器,瞭解人工神經網路 (ANN) 非常重要。人工神經網路是一種資訊處理系統,其機制受到生物神經迴路功能的啟發。人工神經網路擁有許多相互連線的處理單元。以下是人工神經網路的示意圖:
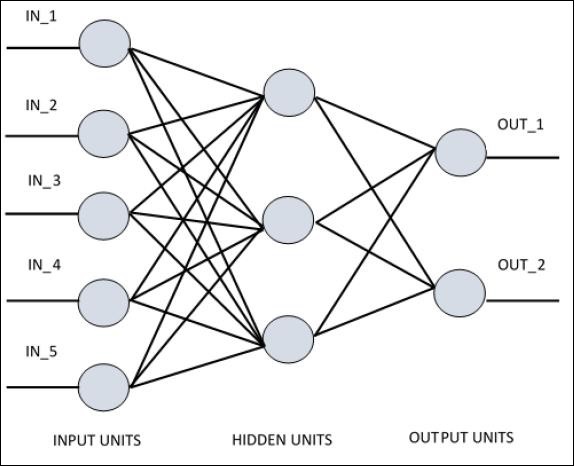
該圖顯示隱藏單元與外部層通訊。而輸入和輸出單元僅透過網路的隱藏層進行通訊。
節點的連線模式、層的總數和輸入與輸出之間節點的級別以及每層的神經元數量定義了神經網路的架構。
有兩種架構型別。這些型別側重於人工神經網路的功能,如下所示:
- 單層感知器
- 多層感知器
單層感知器
單層感知器是第一個提出的神經模型。神經元的本地儲存器的內容包含一個權重向量。單層感知器的計算是在輸入向量之和上執行的,每個輸入向量都乘以權重向量的對應元素。輸出中顯示的值將成為啟用函式的輸入。
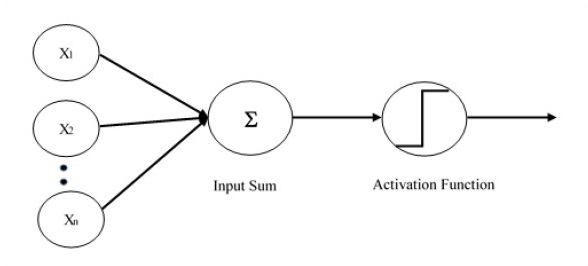
讓我們重點關注使用 TensorFlow 對影像分類問題實現單層感知器。透過“邏輯迴歸”的表示來說明單層感知器的最佳示例。
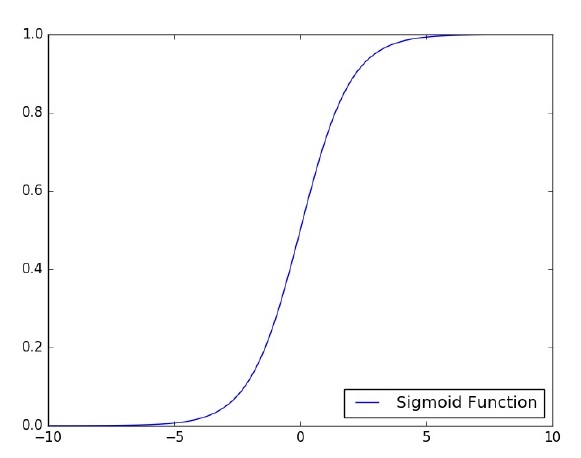
現在,讓我們考慮訓練邏輯迴歸的基本步驟:
在訓練開始時,權重以隨機值初始化。
對於訓練集中的每個元素,都計算誤差,誤差是期望輸出與實際輸出之間的差異。計算出的誤差用於調整權重。
重複此過程,直到整個訓練集上的誤差不大於指定的閾值,或者達到最大迭代次數。
下面提到了用於評估邏輯迴歸的完整程式碼:
# Import MINST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)
import tensorflow as tf
import matplotlib.pyplot as plt
# Parameters
learning_rate = 0.01
training_epochs = 25
batch_size = 100
display_step = 1
# tf Graph Input
x = tf.placeholder("float", [None, 784]) # mnist data image of shape 28*28 = 784
y = tf.placeholder("float", [None, 10]) # 0-9 digits recognition => 10 classes
# Create model
# Set model weights
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
# Construct model
activation = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax
# Minimize error using cross entropy
cross_entropy = y*tf.log(activation)
cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices = 1))
optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost)
#Plot settings
avg_set = []
epoch_set = []
# Initializing the variables init = tf.initialize_all_variables()
# Launch the graph
with tf.Session() as sess:
sess.run(init)
# Training cycle
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples/batch_size)
# Loop over all batches
for i in range(total_batch):
batch_xs, batch_ys = \ mnist.train.next_batch(batch_size)
# Fit training using batch data sess.run(optimizer, \ feed_dict = {
x: batch_xs, y: batch_ys})
# Compute average loss avg_cost += sess.run(cost, \ feed_dict = {
x: batch_xs, \ y: batch_ys})/total_batch
# Display logs per epoch step
if epoch % display_step == 0:
print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
avg_set.append(avg_cost) epoch_set.append(epoch+1)
print ("Training phase finished")
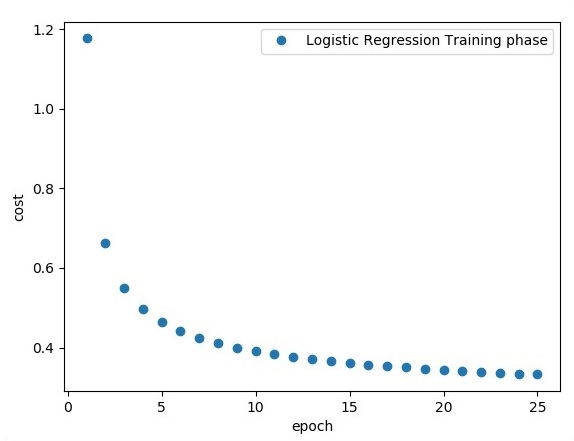
plt.plot(epoch_set,avg_set, 'o', label = 'Logistic Regression Training phase')
plt.ylabel('cost')
plt.xlabel('epoch')
plt.legend()
plt.show()
# Test model
correct_prediction = tf.equal(tf.argmax(activation, 1), tf.argmax(y, 1))
# Calculate accuracy
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print
("Model accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))
輸出
以上程式碼生成以下輸出:
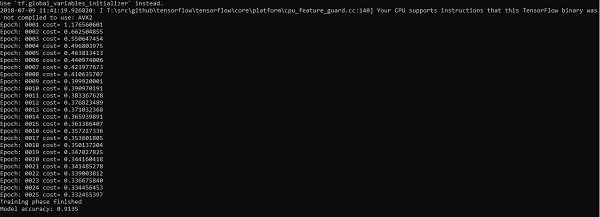
邏輯迴歸被認為是一種預測分析。邏輯迴歸用於描述資料並解釋一個二元因變數與一個或多個名義或自變數之間的關係。
TensorFlow - 線性迴歸
在本章中,我們將重點關注使用 TensorFlow 實現線性迴歸的基本示例。邏輯迴歸或線性迴歸是一種監督機器學習方法,用於對有序離散類別進行分類。我們本章的目標是構建一個模型,使用者可以透過該模型預測預測變數與一個或多個自變數之間的關係。
這兩個變數之間的關係被認為是線性的。如果 y 是因變數,x 被認為是自變數,那麼這兩個變數的線性迴歸關係將如下所示:
Y = Ax+b
我們將設計一種線性迴歸演算法。這將使我們能夠理解以下兩個重要概念:
- 成本函式
- 梯度下降演算法
線性迴歸的示意圖如下所示:

線性迴歸方程的圖形檢視如下所示:
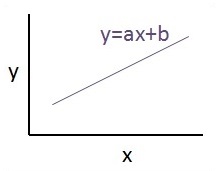
設計線性迴歸演算法的步驟
我們現在將學習有助於設計線性迴歸演算法的步驟。
步驟 1
匯入繪製線性迴歸模組所需的必要模組非常重要。我們首先匯入 Python 庫 NumPy 和 Matplotlib。
import numpy as np import matplotlib.pyplot as plt
步驟 2
定義邏輯迴歸所需的係數數量。
number_of_points = 500 x_point = [] y_point = [] a = 0.22 b = 0.78
步驟 3
迭代變數以生成迴歸方程周圍的 300 個隨機點:
Y = 0.22x+0.78
for i in range(number_of_points): x = np.random.normal(0.0,0.5) y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) y_point.append([y])
步驟 4
使用 Matplotlib 檢視生成的點。
fplt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() plt.show()
邏輯迴歸的完整程式碼如下所示:
import numpy as np import matplotlib.pyplot as plt number_of_points = 500 x_point = [] y_point = [] a = 0.22 b = 0.78 for i in range(number_of_points): x = np.random.normal(0.0,0.5) y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) y_point.append([y]) plt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() plt.show()
作為輸入獲取的點數被視為輸入資料。
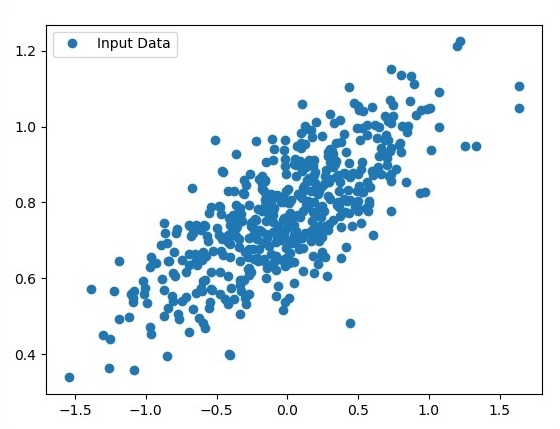
TensorFlow - TFLearn 及其安裝
TFLearn 可以定義為 TensorFlow 框架中使用的模組化且透明的深度學習方面。TFLearn 的主要動機是為 TensorFlow 提供更高級別的 API,以促進和展示新的實驗。
考慮以下 TFLearn 的重要功能:
TFLearn 易於使用和理解。
它包括易於構建高度模組化網路層、最佳化器和嵌入其中的各種指標的概念。
它包括與 TensorFlow 工作系統的完全透明性。
它包括強大的輔助函式來訓練內建張量,這些張量接受多個輸入、輸出和最佳化器。
它包括簡單而漂亮的圖形視覺化。
圖形視覺化包括權重、梯度和啟用的各種詳細資訊。
透過執行以下命令安裝 TFLearn:
pip install tflearn
執行上述程式碼後,將生成以下輸出:
以下插圖顯示了使用隨機森林分類器實現 TFLearn:
from __future__ import division, print_function, absolute_import
#TFLearn module implementation
import tflearn
from tflearn.estimators import RandomForestClassifier
# Data loading and pre-processing with respect to dataset
import tflearn.datasets.mnist as mnist
X, Y, testX, testY = mnist.load_data(one_hot = False)
m = RandomForestClassifier(n_estimators = 100, max_nodes = 1000)
m.fit(X, Y, batch_size = 10000, display_step = 10)
print("Compute the accuracy on train data:")
print(m.evaluate(X, Y, tflearn.accuracy_op))
print("Compute the accuracy on test set:")
print(m.evaluate(testX, testY, tflearn.accuracy_op))
print("Digits for test images id 0 to 5:")
print(m.predict(testX[:5]))
print("True digits:")
print(testY[:5])
TensorFlow - CNN 和 RNN 的區別
在本章中,我們將重點關注 CNN 和 RNN 之間的區別:
| CNN | RNN |
|---|---|
| 它適用於空間資料,例如影像。 | RNN 適用於時間資料,也稱為順序資料。 |
| CNN 被認為比 RNN 更強大。 | 與 CNN 相比,RNN 的功能相容性較差。 |
| 此網路採用固定大小的輸入並生成固定大小的輸出。 | RNN 可以處理任意輸入/輸出長度。 |
| CNN 是一種前饋人工神經網路,具有多層感知器的變體,旨在使用最少的預處理量。 | 與前饋神經網路不同,RNN 可以利用其內部記憶來處理任意輸入序列。 |
| CNN 利用神經元之間的連線模式。這受到動物視覺皮層的組織結構的啟發,動物視覺皮層的單個神經元以某種方式排列,以便對視覺場的重疊區域做出反應。 | 迴圈神經網路使用時間序列資訊 - 使用者上次說了什麼會影響他/她接下來會說什麼。 |
| CNN 非常適合影像和影片處理。 | RNN 非常適合文字和語音分析。 |
下圖顯示了 CNN 和 RNN 的示意圖 -
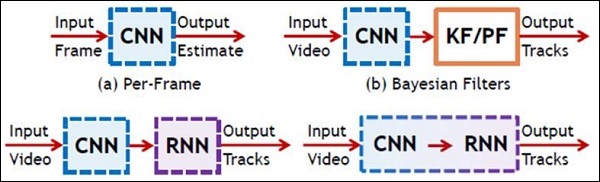
TensorFlow - Keras
Keras 是一個緊湊、易於學習的高階 Python 庫,執行在 TensorFlow 框架之上。它專注於理解深度學習技術,例如為神經網路建立層,同時保持形狀和數學細節的概念。框架的建立可以分為以下兩種型別 -
- 順序 API
- 函式式 API
考慮以下八個步驟在 Keras 中建立深度學習模型 -
- 載入資料
- 預處理載入的資料
- 模型定義
- 編譯模型
- 擬合指定的模型
- 評估模型
- 做出所需的預測
- 儲存模型
我們將使用 Jupyter Notebook 來執行和顯示輸出,如下所示 -
步驟 1 - 首先載入資料並預處理載入的資料,以執行深度學習模型。
import warnings
warnings.filterwarnings('ignore')
import numpy as np
np.random.seed(123) # for reproducibility
from keras.models import Sequential
from keras.layers import Flatten, MaxPool2D, Conv2D, Dense, Reshape, Dropout
from keras.utils import np_utils
Using TensorFlow backend.
from keras.datasets import mnist
# Load pre-shuffled MNIST data into train and test sets
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(X_train.shape[0], 28, 28, 1)
X_test = X_test.reshape(X_test.shape[0], 28, 28, 1)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
Y_train = np_utils.to_categorical(y_train, 10)
Y_test = np_utils.to_categorical(y_test, 10)
此步驟可以定義為“匯入庫和模組”,這意味著所有庫和模組都作為初始步驟匯入。
步驟 2 - 在此步驟中,我們將定義模型架構 -
model = Sequential() model.add(Conv2D(32, 3, 3, activation = 'relu', input_shape = (28,28,1))) model.add(Conv2D(32, 3, 3, activation = 'relu')) model.add(MaxPool2D(pool_size = (2,2))) model.add(Dropout(0.25)) model.add(Flatten()) model.add(Dense(128, activation = 'relu')) model.add(Dropout(0.5)) model.add(Dense(10, activation = 'softmax'))
步驟 3 - 現在讓我們編譯指定的模型 -
model.compile(loss = 'categorical_crossentropy', optimizer = 'adam', metrics = ['accuracy'])
步驟 4 - 我們現在將使用訓練資料擬合模型 -
model.fit(X_train, Y_train, batch_size = 32, epochs = 10, verbose = 1)
建立的迭代輸出如下 -
Epoch 1/10 60000/60000 [==============================] - 65s - loss: 0.2124 - acc: 0.9345 Epoch 2/10 60000/60000 [==============================] - 62s - loss: 0.0893 - acc: 0.9740 Epoch 3/10 60000/60000 [==============================] - 58s - loss: 0.0665 - acc: 0.9802 Epoch 4/10 60000/60000 [==============================] - 62s - loss: 0.0571 - acc: 0.9830 Epoch 5/10 60000/60000 [==============================] - 62s - loss: 0.0474 - acc: 0.9855 Epoch 6/10 60000/60000 [==============================] - 59s - loss: 0.0416 - acc: 0.9871 Epoch 7/10 60000/60000 [==============================] - 61s - loss: 0.0380 - acc: 0.9877 Epoch 8/10 60000/60000 [==============================] - 63s - loss: 0.0333 - acc: 0.9895 Epoch 9/10 60000/60000 [==============================] - 64s - loss: 0.0325 - acc: 0.9898 Epoch 10/10 60000/60000 [==============================] - 60s - loss: 0.0284 - acc: 0.9910
TensorFlow - 分散式計算
本章將重點介紹如何開始使用分散式 TensorFlow。目的是幫助開發人員理解反覆出現的分散式 TF 基本概念,例如 TF 伺服器。我們將使用 Jupyter Notebook 來評估分散式 TensorFlow。TensorFlow 的分散式計算實現如下 -
步驟 1 - 匯入分散式計算所需的必要模組 -
import tensorflow as tf
步驟 2 - 建立一個具有一個節點的 TensorFlow 叢集。讓此節點負責一個名為“worker”的任務,該任務將在 localhost:2222 上執行一個操作。
cluster_spec = tf.train.ClusterSpec({'worker' : ['localhost:2222']})
server = tf.train.Server(cluster_spec)
server.target
以上指令碼生成以下輸出 -
'grpc://:2222' The server is currently running.
步驟 3 - 可以透過執行以下命令來計算相應的會話的伺服器配置 -
server.server_def
以上命令生成以下輸出 -
cluster {
job {
name: "worker"
tasks {
value: "localhost:2222"
}
}
}
job_name: "worker"
protocol: "grpc"
步驟 4 - 啟動一個 TensorFlow 會話,其執行引擎為伺服器。使用 TensorFlow 建立一個本地伺服器,並使用lsof找出伺服器的位置。
sess = tf.Session(target = server.target) server = tf.train.Server.create_local_server()
步驟 5 - 檢視此會話中可用的裝置,並關閉相應的會話。
devices = sess.list_devices() for d in devices: print(d.name) sess.close()
以上命令生成以下輸出 -
/job:worker/replica:0/task:0/device:CPU:0
TensorFlow - 匯出
在這裡,我們將重點關注 TensorFlow 中的 MetaGraph 形成。這將有助於我們理解 TensorFlow 中的匯出模組。MetaGraph 包含基本資訊,這些資訊是訓練、執行評估或在先前訓練的圖上執行推理所必需的。
以下是相同的程式碼片段 -
def export_meta_graph(filename = None, collection_list = None, as_text = False):
"""this code writes `MetaGraphDef` to save_path/filename.
Arguments:
filename: Optional meta_graph filename including the path. collection_list:
List of string keys to collect. as_text: If `True`,
writes the meta_graph as an ASCII proto.
Returns:
A `MetaGraphDef` proto. """
下面提到了一個典型的用法模型 -
# Build the model ... with tf.Session() as sess: # Use the model ... # Export the model to /tmp/my-model.meta. meta_graph_def = tf.train.export_meta_graph(filename = '/tmp/my-model.meta')
TensorFlow - 多層感知器學習
多層感知器定義了人工神經網路中最複雜的架構。它基本上由多層感知器組成。
多層感知器學習的圖示如下所示 -
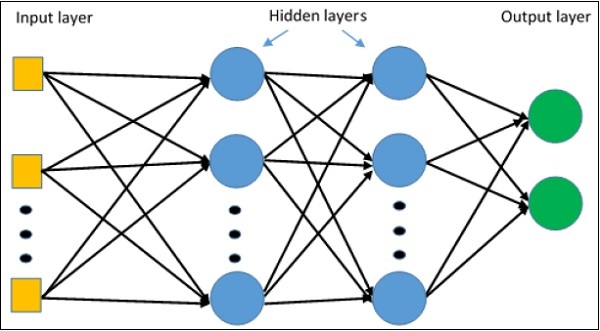
MLP 網路通常用於監督學習格式。MLP 網路的典型學習演算法也稱為反向傳播演算法。
現在,我們將重點關注使用 MLP 解決影像分類問題的實現。
# Import MINST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)
import tensorflow as tf
import matplotlib.pyplot as plt
# Parameters
learning_rate = 0.001
training_epochs = 20
batch_size = 100
display_step = 1
# Network Parameters
n_hidden_1 = 256
# 1st layer num features
n_hidden_2 = 256 # 2nd layer num features
n_input = 784 # MNIST data input (img shape: 28*28) n_classes = 10
# MNIST total classes (0-9 digits)
# tf Graph input
x = tf.placeholder("float", [None, n_input])
y = tf.placeholder("float", [None, n_classes])
# weights layer 1
h = tf.Variable(tf.random_normal([n_input, n_hidden_1])) # bias layer 1
bias_layer_1 = tf.Variable(tf.random_normal([n_hidden_1]))
# layer 1 layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, h), bias_layer_1))
# weights layer 2
w = tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2]))
# bias layer 2
bias_layer_2 = tf.Variable(tf.random_normal([n_hidden_2]))
# layer 2
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, w), bias_layer_2))
# weights output layer
output = tf.Variable(tf.random_normal([n_hidden_2, n_classes]))
# biar output layer
bias_output = tf.Variable(tf.random_normal([n_classes])) # output layer
output_layer = tf.matmul(layer_2, output) + bias_output
# cost function
cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
logits = output_layer, labels = y))
#cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(output_layer, y))
# optimizer
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost)
# optimizer = tf.train.GradientDescentOptimizer(
learning_rate = learning_rate).minimize(cost)
# Plot settings
avg_set = []
epoch_set = []
# Initializing the variables
init = tf.global_variables_initializer()
# Launch the graph
with tf.Session() as sess:
sess.run(init)
# Training cycle
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples / batch_size)
# Loop over all batches
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# Fit training using batch data sess.run(optimizer, feed_dict = {
x: batch_xs, y: batch_ys})
# Compute average loss
avg_cost += sess.run(cost, feed_dict = {x: batch_xs, y: batch_ys}) / total_batch
# Display logs per epoch step
if epoch % display_step == 0:
print
Epoch:", '%04d' % (epoch + 1), "cost=", "{:.9f}".format(avg_cost)
avg_set.append(avg_cost)
epoch_set.append(epoch + 1)
print
"Training phase finished"
plt.plot(epoch_set, avg_set, 'o', label = 'MLP Training phase')
plt.ylabel('cost')
plt.xlabel('epoch')
plt.legend()
plt.show()
# Test model
correct_prediction = tf.equal(tf.argmax(output_layer, 1), tf.argmax(y, 1))
# Calculate accuracy
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print
"Model Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels})
以上程式碼行生成以下輸出 -
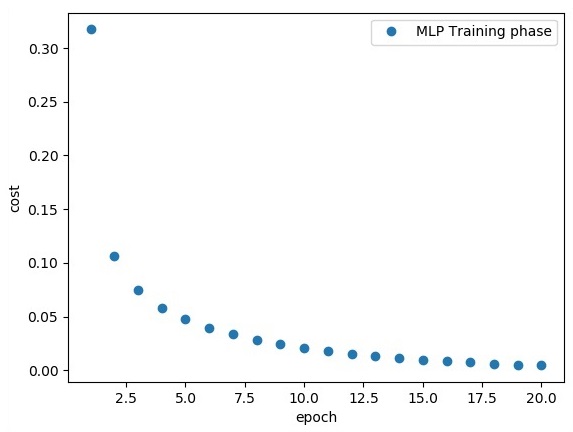
TensorFlow - 感知器的隱藏層
在本章中,我們將重點關注我們必須從稱為 x 和 f(x) 的已知點集中學習的網路。一個隱藏層將構建這個簡單的網路。
感知器隱藏層解釋的程式碼如下所示 -
#Importing the necessary modules
import tensorflow as tf
import numpy as np
import math, random
import matplotlib.pyplot as plt
np.random.seed(1000)
function_to_learn = lambda x: np.cos(x) + 0.1*np.random.randn(*x.shape)
layer_1_neurons = 10
NUM_points = 1000
#Training the parameters
batch_size = 100
NUM_EPOCHS = 1500
all_x = np.float32(np.random.uniform(-2*math.pi, 2*math.pi, (1, NUM_points))).T
np.random.shuffle(all_x)
train_size = int(900)
#Training the first 700 points in the given set x_training = all_x[:train_size]
y_training = function_to_learn(x_training)
#Training the last 300 points in the given set x_validation = all_x[train_size:]
y_validation = function_to_learn(x_validation)
plt.figure(1)
plt.scatter(x_training, y_training, c = 'blue', label = 'train')
plt.scatter(x_validation, y_validation, c = 'pink', label = 'validation')
plt.legend()
plt.show()
X = tf.placeholder(tf.float32, [None, 1], name = "X")
Y = tf.placeholder(tf.float32, [None, 1], name = "Y")
#first layer
#Number of neurons = 10
w_h = tf.Variable(
tf.random_uniform([1, layer_1_neurons],\ minval = -1, maxval = 1, dtype = tf.float32))
b_h = tf.Variable(tf.zeros([1, layer_1_neurons], dtype = tf.float32))
h = tf.nn.sigmoid(tf.matmul(X, w_h) + b_h)
#output layer
#Number of neurons = 10
w_o = tf.Variable(
tf.random_uniform([layer_1_neurons, 1],\ minval = -1, maxval = 1, dtype = tf.float32))
b_o = tf.Variable(tf.zeros([1, 1], dtype = tf.float32))
#build the model
model = tf.matmul(h, w_o) + b_o
#minimize the cost function (model - Y)
train_op = tf.train.AdamOptimizer().minimize(tf.nn.l2_loss(model - Y))
#Start the Learning phase
sess = tf.Session() sess.run(tf.initialize_all_variables())
errors = []
for i in range(NUM_EPOCHS):
for start, end in zip(range(0, len(x_training), batch_size),\
range(batch_size, len(x_training), batch_size)):
sess.run(train_op, feed_dict = {X: x_training[start:end],\ Y: y_training[start:end]})
cost = sess.run(tf.nn.l2_loss(model - y_validation),\ feed_dict = {X:x_validation})
errors.append(cost)
if i%100 == 0:
print("epoch %d, cost = %g" % (i, cost))
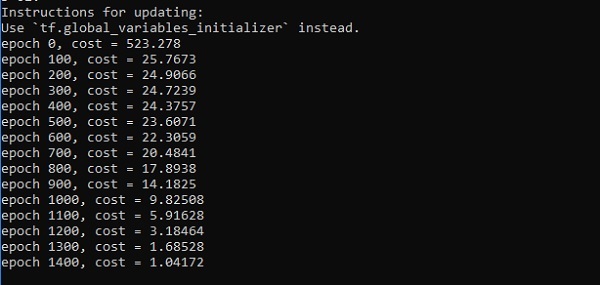
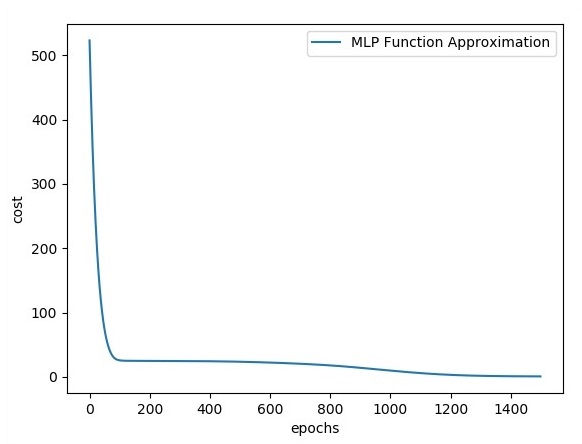
plt.plot(errors,label='MLP Function Approximation') plt.xlabel('epochs')
plt.ylabel('cost')
plt.legend()
plt.show()
輸出
以下是函式層近似的表示 -
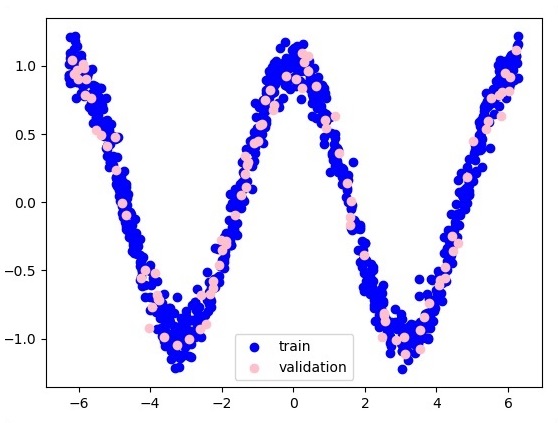
這裡兩個資料以 W 的形狀表示。這兩個資料是:訓練和驗證,它們以不同的顏色表示,如圖例部分所示。
TensorFlow - 最佳化器
最佳化器是擴充套件類,其中包含用於訓練特定模型的附加資訊。最佳化器類使用給定引數進行初始化,但重要的是要記住不需要張量。最佳化器用於提高訓練特定模型的速度和效能。
TensorFlow 的基本最佳化器是 -
tf.train.Optimizer
此類在 tensorflow/python/training/optimizer.py 的指定路徑中定義。
以下是 TensorFlow 中的一些最佳化器 -
- 隨機梯度下降
- 帶有梯度裁剪的隨機梯度下降
- 動量
- Nesterov 動量
- Adagrad
- Adadelta
- RMSProp
- Adam
- Adamax
- SMORMS3
我們將重點關注隨機梯度下降。為其建立最佳化器的圖示如下所示 -
def sgd(cost, params, lr = np.float32(0.01)):
g_params = tf.gradients(cost, params)
updates = []
for param, g_param in zip(params, g_params):
updates.append(param.assign(param - lr*g_param))
return updates
基本引數在特定函式內定義。在我們接下來的章節中,我們將重點關注梯度下降最佳化以及最佳化器的實現。
TensorFlow - XOR 實現
在本章中,我們將學習有關使用 TensorFlow 實現 XOR 的知識。在開始使用 TensorFlow 實現 XOR 之前,讓我們看看 XOR 表的值。這將幫助我們理解加密和解密過程。
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XOR 密碼加密方法基本上用於加密難以用蠻力方法破解的資料,即透過生成與適當金鑰匹配的隨機加密金鑰。
使用 XOR 密碼進行實現的概念是定義一個 XOR 加密金鑰,然後使用此金鑰對指定字串中的字元執行 XOR 操作,使用者嘗試使用此金鑰加密資料。現在我們將重點介紹使用 TensorFlow 實現 XOR,如下所示 -
#Declaring necessary modules
import tensorflow as tf
import numpy as np
"""
A simple numpy implementation of a XOR gate to understand the backpropagation
algorithm
"""
x = tf.placeholder(tf.float64,shape = [4,2],name = "x")
#declaring a place holder for input x
y = tf.placeholder(tf.float64,shape = [4,1],name = "y")
#declaring a place holder for desired output y
m = np.shape(x)[0]#number of training examples
n = np.shape(x)[1]#number of features
hidden_s = 2 #number of nodes in the hidden layer
l_r = 1#learning rate initialization
theta1 = tf.cast(tf.Variable(tf.random_normal([3,hidden_s]),name = "theta1"),tf.float64)
theta2 = tf.cast(tf.Variable(tf.random_normal([hidden_s+1,1]),name = "theta2"),tf.float64)
#conducting forward propagation
a1 = tf.concat([np.c_[np.ones(x.shape[0])],x],1)
#the weights of the first layer are multiplied by the input of the first layer
z1 = tf.matmul(a1,theta1)
#the input of the second layer is the output of the first layer, passed through the
activation function and column of biases is added
a2 = tf.concat([np.c_[np.ones(x.shape[0])],tf.sigmoid(z1)],1)
#the input of the second layer is multiplied by the weights
z3 = tf.matmul(a2,theta2)
#the output is passed through the activation function to obtain the final probability
h3 = tf.sigmoid(z3)
cost_func = -tf.reduce_sum(y*tf.log(h3)+(1-y)*tf.log(1-h3),axis = 1)
#built in tensorflow optimizer that conducts gradient descent using specified
learning rate to obtain theta values
optimiser = tf.train.GradientDescentOptimizer(learning_rate = l_r).minimize(cost_func)
#setting required X and Y values to perform XOR operation
X = [[0,0],[0,1],[1,0],[1,1]]
Y = [[0],[1],[1],[0]]
#initializing all variables, creating a session and running a tensorflow session
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
#running gradient descent for each iteration and printing the hypothesis
obtained using the updated theta values
for i in range(100000):
sess.run(optimiser, feed_dict = {x:X,y:Y})#setting place holder values using feed_dict
if i%100==0:
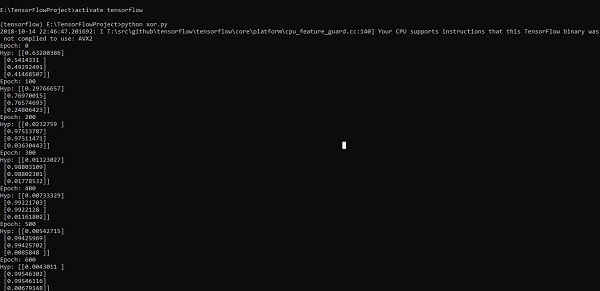
print("Epoch:",i)
print("Hyp:",sess.run(h3,feed_dict = {x:X,y:Y}))
以上程式碼行生成如下截圖所示的輸出 -
TensorFlow - 梯度下降最佳化
梯度下降最佳化被認為是資料科學中的一個重要概念。
考慮以下步驟以瞭解梯度下降最佳化的實現 -
步驟 1
包含必要的模組並透過我們將要定義梯度下降最佳化的 x 和 y 變數進行宣告。
import tensorflow as tf x = tf.Variable(2, name = 'x', dtype = tf.float32) log_x = tf.log(x) log_x_squared = tf.square(log_x) optimizer = tf.train.GradientDescentOptimizer(0.5) train = optimizer.minimize(log_x_squared)
步驟 2
初始化必要的變數並呼叫最佳化器以定義並使用相應的函式呼叫它。
init = tf.initialize_all_variables()
def optimize():
with tf.Session() as session:
session.run(init)
print("starting at", "x:", session.run(x), "log(x)^2:", session.run(log_x_squared))
for step in range(10):
session.run(train)
print("step", step, "x:", session.run(x), "log(x)^2:", session.run(log_x_squared))
optimize()
以上程式碼行生成如下截圖所示的輸出 -
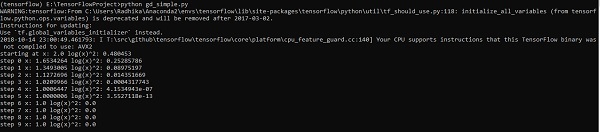
我們可以看到必要的 epoch 和迭代次數已如輸出所示計算出來。
TensorFlow - 構建圖
偏微分方程 (PDE) 是一種微分方程,它涉及具有多個自變數的未知函式的偏導數。關於偏微分方程,我們將重點關注建立新的圖形。
讓我們假設有一個尺寸為 500*500 平方英尺的水池 -
N = 500
現在,我們將計算偏微分方程並使用它形成相應的圖形。考慮以下步驟以計算圖形。
步驟 1 - 匯入用於模擬的庫。
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt
步驟 2 - 包含將 2D 陣列轉換為卷積核和簡化的 2D 卷積運算的函式。
def make_kernel(a): a = np.asarray(a) a = a.reshape(list(a.shape) + [1,1]) return tf.constant(a, dtype=1) def simple_conv(x, k): """A simplified 2D convolution operation""" x = tf.expand_dims(tf.expand_dims(x, 0), -1) y = tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding = 'SAME') return y[0, :, :, 0] def laplace(x): """Compute the 2D laplacian of an array""" laplace_k = make_kernel([[0.5, 1.0, 0.5], [1.0, -6., 1.0], [0.5, 1.0, 0.5]]) return simple_conv(x, laplace_k) sess = tf.InteractiveSession()
步驟 3 - 包含迭代次數並計算圖形以相應地顯示記錄。
N = 500
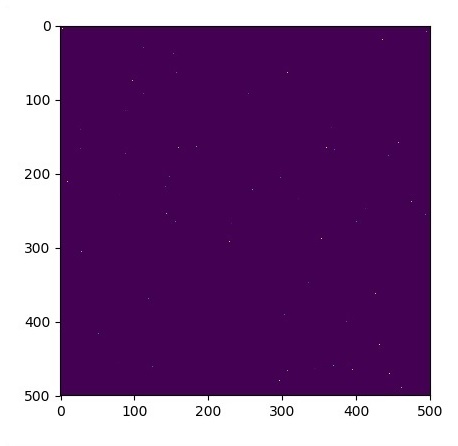
# Initial Conditions -- some rain drops hit a pond
# Set everything to zero
u_init = np.zeros([N, N], dtype = np.float32)
ut_init = np.zeros([N, N], dtype = np.float32)
# Some rain drops hit a pond at random points
for n in range(100):
a,b = np.random.randint(0, N, 2)
u_init[a,b] = np.random.uniform()
plt.imshow(u_init)
plt.show()
# Parameters:
# eps -- time resolution
# damping -- wave damping
eps = tf.placeholder(tf.float32, shape = ())
damping = tf.placeholder(tf.float32, shape = ())
# Create variables for simulation state
U = tf.Variable(u_init)
Ut = tf.Variable(ut_init)
# Discretized PDE update rules
U_ = U + eps * Ut
Ut_ = Ut + eps * (laplace(U) - damping * Ut)
# Operation to update the state
step = tf.group(U.assign(U_), Ut.assign(Ut_))
# Initialize state to initial conditions
tf.initialize_all_variables().run()
# Run 1000 steps of PDE
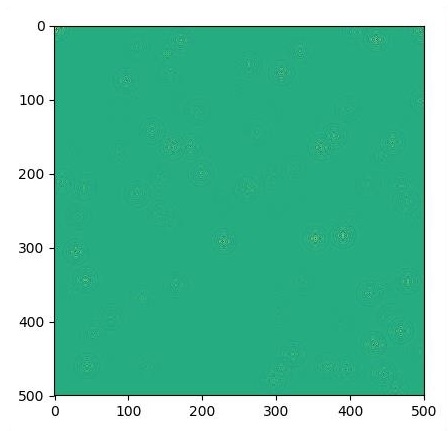
for i in range(1000):
# Step simulation
step.run({eps: 0.03, damping: 0.04})
# Visualize every 50 steps
if i % 500 == 0:
plt.imshow(U.eval())
plt.show()
圖形繪製如下所示 -
使用 TensorFlow 進行影像識別
TensorFlow 包含一個特殊的影像識別功能,這些影像儲存在特定資料夾中。對於相對相同的影像,將很容易為安全目的實現此邏輯。
影像識別程式碼實現的資料夾結構如下所示 -
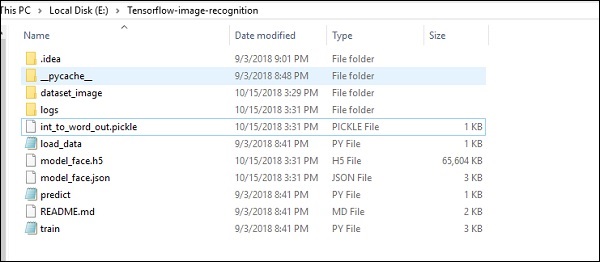
dataset_image 包含需要載入的相關影像。我們將重點關注使用我們定義的徽標進行影像識別。影像使用“load_data.py”指令碼載入,這有助於記錄其中的各種影像識別模組。
import pickle
from sklearn.model_selection import train_test_split
from scipy import misc
import numpy as np
import os
label = os.listdir("dataset_image")
label = label[1:]
dataset = []
for image_label in label:
images = os.listdir("dataset_image/"+image_label)
for image in images:
img = misc.imread("dataset_image/"+image_label+"/"+image)
img = misc.imresize(img, (64, 64))
dataset.append((img,image_label))
X = []
Y = []
for input,image_label in dataset:
X.append(input)
Y.append(label.index(image_label))
X = np.array(X)
Y = np.array(Y)
X_train,y_train, = X,Y
data_set = (X_train,y_train)
save_label = open("int_to_word_out.pickle","wb")
pickle.dump(label, save_label)
save_label.close()
影像的訓練有助於將可識別的模式儲存在指定的資料夾中。
import numpy
import matplotlib.pyplot as plt
from keras.layers import Dropout
from keras.layers import Flatten
from keras.constraints import maxnorm
from keras.optimizers import SGD
from keras.layers import Conv2D
from keras.layers.convolutional import MaxPooling2D
from keras.utils import np_utils
from keras import backend as K
import load_data
from keras.models import Sequential
from keras.layers import Dense
import keras
K.set_image_dim_ordering('tf')
# fix random seed for reproducibility
seed = 7
numpy.random.seed(seed)
# load data
(X_train,y_train) = load_data.data_set
# normalize inputs from 0-255 to 0.0-1.0
X_train = X_train.astype('float32')
#X_test = X_test.astype('float32')
X_train = X_train / 255.0
#X_test = X_test / 255.0
# one hot encode outputs
y_train = np_utils.to_categorical(y_train)
#y_test = np_utils.to_categorical(y_test)
num_classes = y_train.shape[1]
# Create the model
model = Sequential()
model.add(Conv2D(32, (3, 3), input_shape = (64, 64, 3), padding = 'same',
activation = 'relu', kernel_constraint = maxnorm(3)))
model.add(Dropout(0.2))
model.add(Conv2D(32, (3, 3), activation = 'relu', padding = 'same',
kernel_constraint = maxnorm(3)))
model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Flatten())
model.add(Dense(512, activation = 'relu', kernel_constraint = maxnorm(3)))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation = 'softmax'))
# Compile model
epochs = 10
lrate = 0.01
decay = lrate/epochs
sgd = SGD(lr = lrate, momentum = 0.9, decay = decay, nesterov = False)
model.compile(loss = 'categorical_crossentropy', optimizer = sgd, metrics = ['accuracy'])
print(model.summary())
#callbacks = [keras.callbacks.EarlyStopping(
monitor = 'val_loss', min_delta = 0, patience = 0, verbose = 0, mode = 'auto')]
callbacks = [keras.callbacks.TensorBoard(log_dir='./logs',
histogram_freq = 0, batch_size = 32, write_graph = True, write_grads = False,
write_images = True, embeddings_freq = 0, embeddings_layer_names = None,
embeddings_metadata = None)]
# Fit the model
model.fit(X_train, y_train, epochs = epochs,
batch_size = 32,shuffle = True,callbacks = callbacks)
# Final evaluation of the model
scores = model.evaluate(X_train, y_train, verbose = 0)
print("Accuracy: %.2f%%" % (scores[1]*100))
# serialize model to JSONx
model_json = model.to_json()
with open("model_face.json", "w") as json_file:
json_file.write(model_json)
# serialize weights to HDF5
model.save_weights("model_face.h5")
print("Saved model to disk")
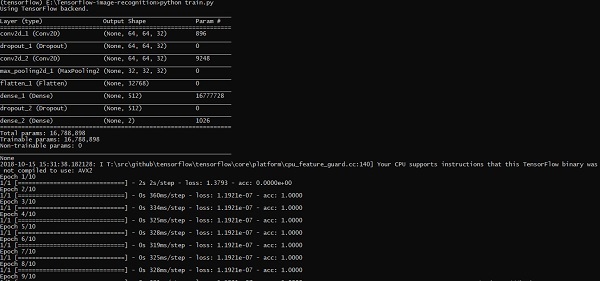
以上程式碼行生成如下所示的輸出 -
神經網路訓練建議
在本章中,我們將瞭解可以使用 TensorFlow 框架實現的神經網路訓練的各個方面。
以下是可以評估的十項建議 -
反向傳播
反向傳播是一種計算偏導數的簡單方法,它包括最適合神經網路的基本合成形式。
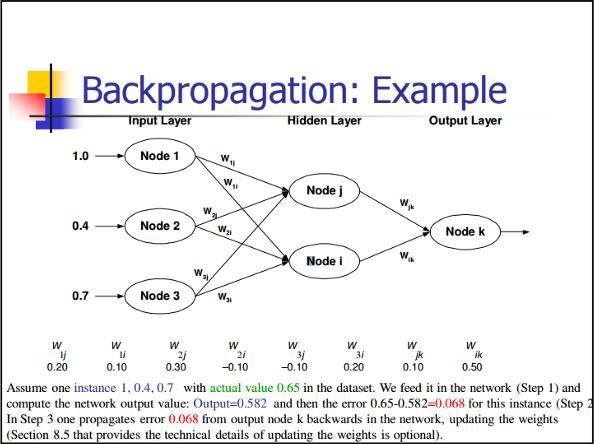
隨機梯度下降
在隨機梯度下降中,**批次**是使用者在單個迭代中用於計算梯度的示例總數。到目前為止,假設批次已成為整個資料集。最好的說明是在 Google 規模下工作;資料集通常包含數十億甚至數百億個示例。
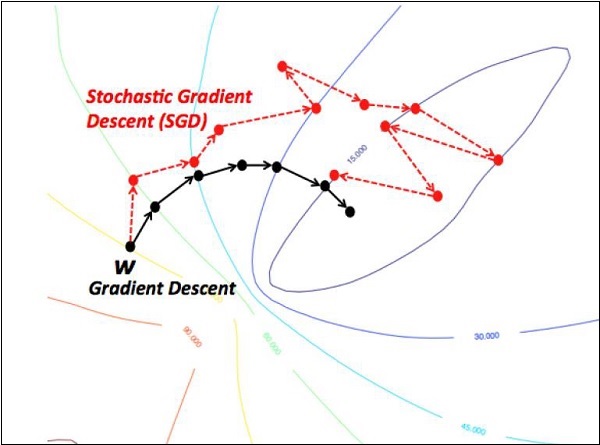
學習率衰減
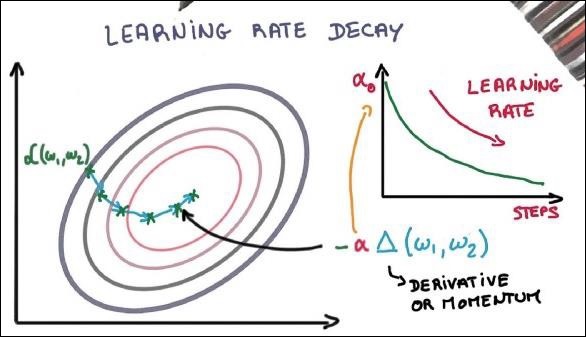
調整學習率是梯度下降最佳化最重要的功能之一。這對 TensorFlow 實現至關重要。
Dropout
具有大量引數的深度神經網路形成了強大的機器學習系統。但是,過擬合是此類網路中的一個嚴重問題。
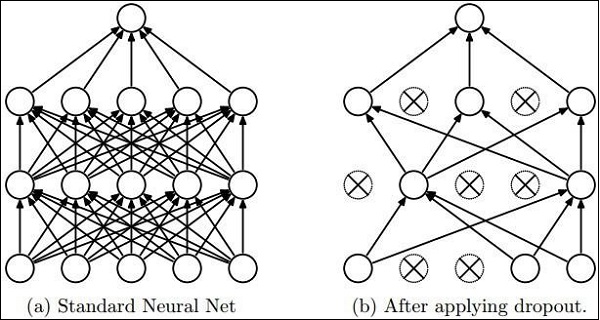
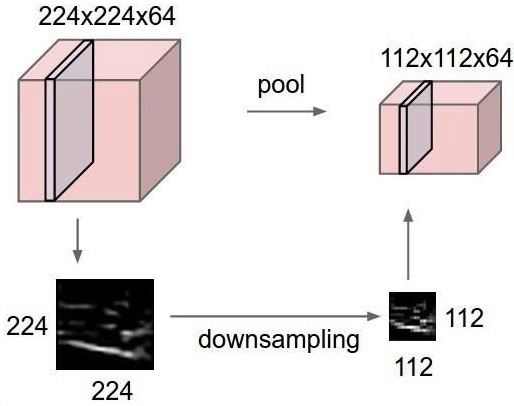
最大池化
最大池化是一個基於樣本的離散化過程。目的是對輸入表示進行下采樣,這在必要的假設下降低了維度。
長短期記憶 (LSTM)
LSTM 控制對在指定神經元中應採用哪些輸入的決策。它包括控制決定應該計算什麼以及應該生成什麼輸出。