R - 正態分佈

在從獨立來源隨機收集的資料中，通常觀察到資料的分佈是正態的。這意味著，在繪製一個圖表，其中變數的值位於橫軸上，而值的數量位於縱軸上時，我們得到一個鐘形曲線。曲線的中心表示資料集的平均值。在圖表中，50% 的值位於平均值的左側，而另外 50% 的值位於圖表的右側。這在統計學中被稱為正態分佈。

R 有四個內建函式來生成正態分佈。它們在下面描述。

dnorm(x, mean, sd)
pnorm(x, mean, sd)
qnorm(p, mean, sd)
rnorm(n, mean, sd)

以下是上述函式中使用的引數的描述：

• x 是一個數字向量。

• p 是一個機率向量。

• n 是觀測值的數量（樣本量）。

• mean 是樣本資料的平均值。其預設值為零。

• sd 是標準差。其預設值為 1。

dnorm()

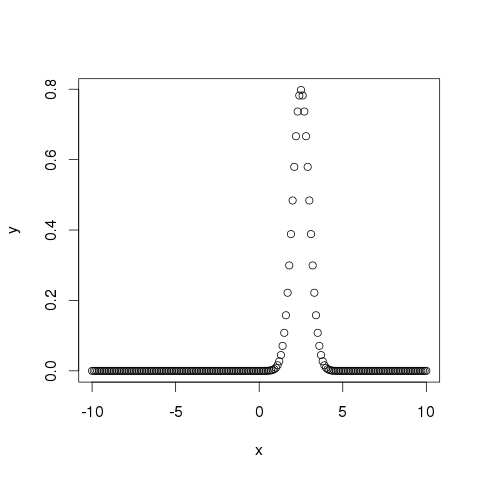
此函式給出了給定均值和標準差下每個點的機率分佈的高度。

# Create a sequence of numbers between -10 and 10 incrementing by 0.1.
x <- seq(-10, 10, by = .1)

# Choose the mean as 2.5 and standard deviation as 0.5.
y <- dnorm(x, mean = 2.5, sd = 0.5)

# Give the chart file a name.
png(file = "dnorm.png")

plot(x,y)

# Save the file.
dev.off()

當我們執行以上程式碼時，它會產生以下結果：

pnorm()

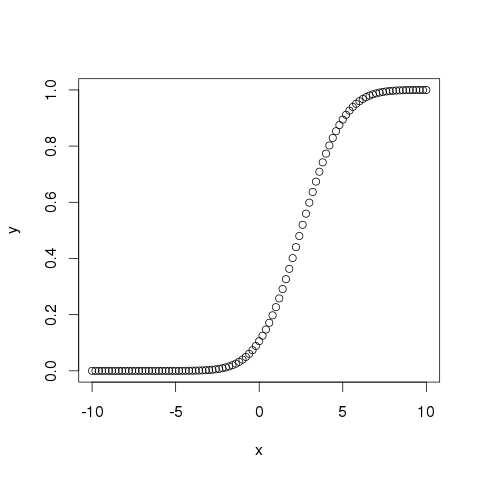
此函式給出了正態分佈的隨機數小於給定數字的值的機率。它也稱為“累積分佈函式”。

# Create a sequence of numbers between -10 and 10 incrementing by 0.2.
x <- seq(-10,10,by = .2)
 
# Choose the mean as 2.5 and standard deviation as 2. 
y <- pnorm(x, mean = 2.5, sd = 2)

# Give the chart file a name.
png(file = "pnorm.png")

# Plot the graph.
plot(x,y)

# Save the file.
dev.off()

當我們執行以上程式碼時，它會產生以下結果：

qnorm()

此函式採用機率值並給出一個其累積值與機率值匹配的數字。

# Create a sequence of probability values incrementing by 0.02.
x <- seq(0, 1, by = 0.02)

# Choose the mean as 2 and standard deviation as 3.
y <- qnorm(x, mean = 2, sd = 1)

# Give the chart file a name.
png(file = "qnorm.png")

# Plot the graph.
plot(x,y)

# Save the file.
dev.off()

當我們執行以上程式碼時，它會產生以下結果：

rnorm()

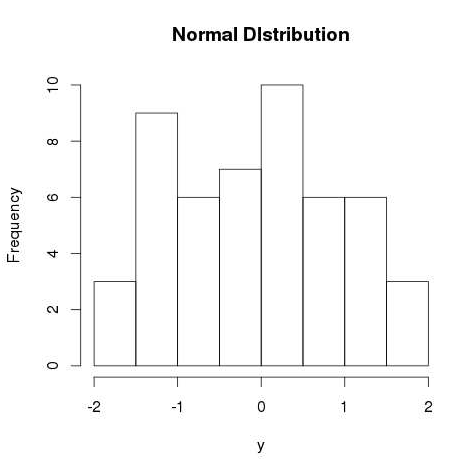
此函式用於生成分佈為正態的隨機數。它將樣本量作為輸入並生成那麼多隨機數。我們繪製一個直方圖來顯示生成的數字的分佈。

# Create a sample of 50 numbers which are normally distributed.
y <- rnorm(50)

# Give the chart file a name.
png(file = "rnorm.png")

# Plot the histogram for this sample.
hist(y, main = "Normal DIstribution")

# Save the file.
dev.off()

當我們執行以上程式碼時，它會產生以下結果：