R - 二項分佈

二項分佈模型用於計算在多次實驗中，只有兩種可能結果的事件成功的機率。例如，拋硬幣總是得到正面或反面。二項分佈用於估計在連續拋擲硬幣 10 次中恰好得到 3 個正面的機率。

R 有四個內建函式可以生成二項分佈。它們描述如下。

dbinom(x, size, prob)
pbinom(x, size, prob)
qbinom(p, size, prob)
rbinom(n, size, prob)

以下是所用引數的描述：

• x 是一個數字向量。

• p 是一個機率向量。

• n 是觀測數。

• size 是試驗次數。

• prob 是每次試驗成功的機率。

dbinom()

此函式給出每個點的機率密度分佈。

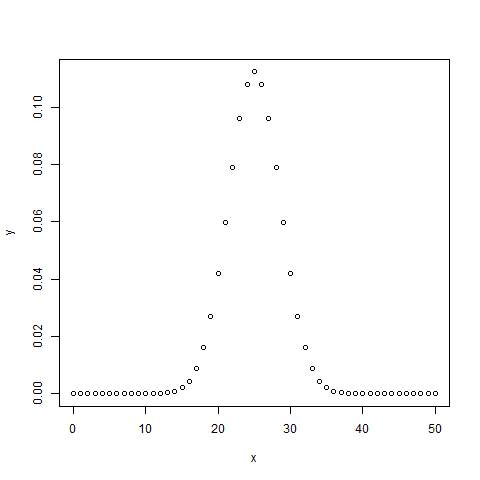
# Create a sample of 50 numbers which are incremented by 1.
x <- seq(0,50,by = 1)

# Create the binomial distribution.
y <- dbinom(x,50,0.5)

# Give the chart file a name.
png(file = "dbinom.png")

# Plot the graph for this sample.
plot(x,y)

# Save the file.
dev.off()

當我們執行上述程式碼時，它會產生以下結果：

pbinom()

此函式給出事件的累積機率。它是一個表示機率的單個值。

# Probability of getting 26 or less heads from a 51 tosses of a coin.
x <- pbinom(26,51,0.5)

print(x)

當我們執行上述程式碼時，它會產生以下結果：

[1] 0.610116

qbinom()

此函式取機率值並給出一個其累積值與機率值匹配的數字。

# How many heads will have a probability of 0.25 will come out when a coin
# is tossed 51 times.
x <- qbinom(0.25,51,1/2)

print(x)

當我們執行上述程式碼時，它會產生以下結果：

[1] 23

rbinom()

此函式根據給定樣本生成給定機率的所需數量的隨機值。

# Find 8 random values from a sample of 150 with probability of 0.4.
x <- rbinom(8,150,.4)

print(x)

當我們執行上述程式碼時，它會產生以下結果：

[1] 58 61 59 66 55 60 61 67