資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究證明從圓外一點引出的兩條切線之間的夾角與連線切點並在圓心處所成的角互補。
待辦事項
我們需要證明從圓外一點引出的兩條切線之間的夾角與連線切點並在圓心處所成的角互補。
解答
設 $PA$ 和 $PB$ 是兩條切線，$A$ 和 $B$ 是切點的座標。
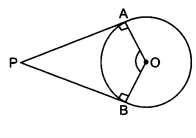
$\mathrm{OA} \perp \mathrm{AP}$
$\mathrm{OB} \perp \mathrm{BP}$
$\angle \mathrm{OAP}=\angle \mathrm{OBP}=90^{\circ}$
在四邊形 $\mathrm{OAPB}$ 中
$\angle \mathrm{OAP}+\angle \mathrm{OBP}+\angle \mathrm{APB}+\angle \mathrm{AOB}=360^{\circ}$
$90^{\circ}+90^{\circ}+\angle \mathrm{APB}+\angle \mathrm{AOB}=360^{\circ}$
$\angle \mathrm{APB}+\angle \mathrm{AOB}=360^{\circ}-180^{\circ}$
$=180^{\circ}$
因此，
$\angle \mathrm{APB}$ 和 $\angle \mathrm{AOB}$ 是互補角。
證畢。
更新於: 2022年10月10日
113 次瀏覽
廣告