資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
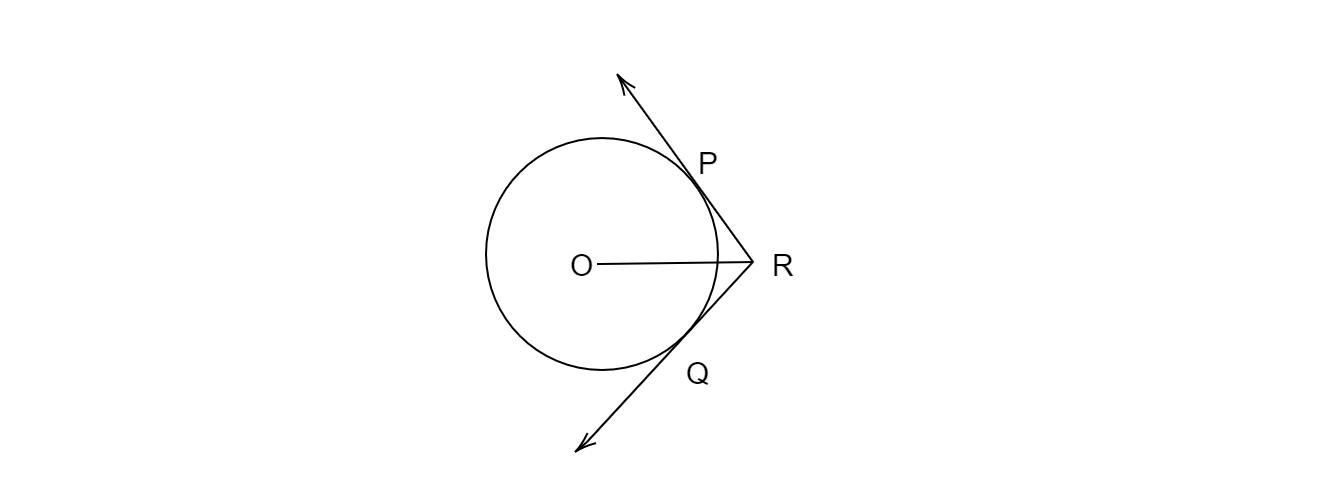
法律研究在下圖中，從圓外一點 R 引兩條切線 RQ 和 RP 到圓心為 O 的圓，如果∠PRQ=120°，則證明 OR=PR+RQ。
"\n
已知：從圓外一點 R 引兩條切線 RQ 和 RP 到圓心為 O 的圓，如果∠PRQ = 120°。
要求：證明 OR = PR + RQ。
解答
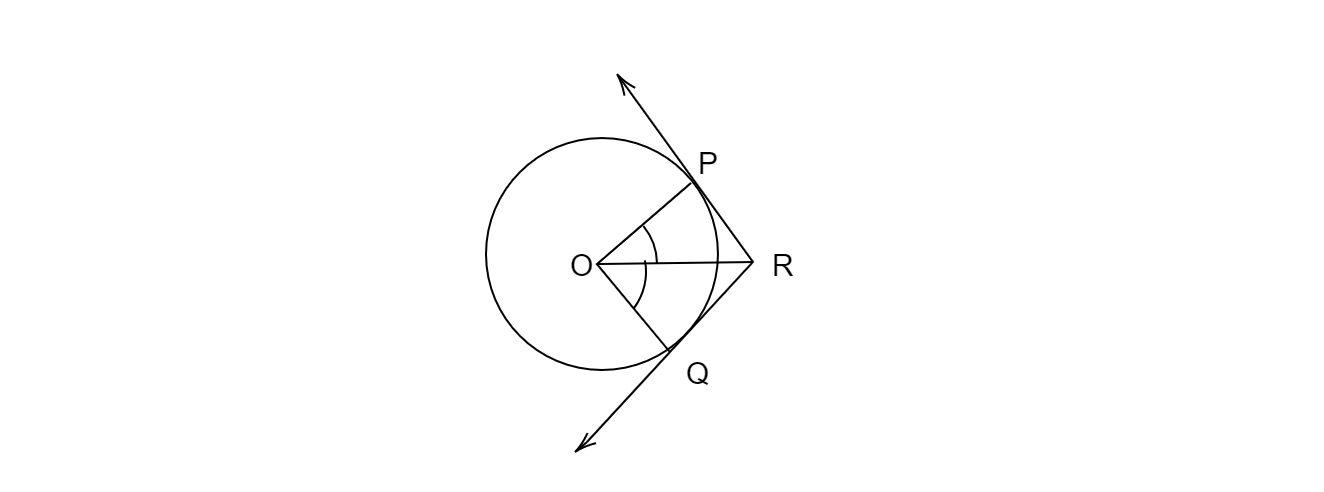
連線 OR。
已知連線圓心和外一點的直線是切線之間角的角平分線。
這裡給出∠PRQ = 120°
∠PRO=∠QRO=120°/2 =60°
我們也知道，從圓外一點引出的切線的長度相等。
因此，PR=RQ。
連線 OP 和 OQ。
由於 OP 和 OQ 是從圓心 O 引出的半徑，
OP⊥PR 和 OQ⊥RQ。
因此，△OPR 和 △OQR 是直角全等三角形。
∴ ∠POR=90°-∠PRO=90°-60°=30°
同樣地，∠QOR=90°-60°=30°
sin(∠POR) =sin30° =1/2 =PR/OR
⇒ 1/2 =PR/OR
⇒ OR=2PR
⇒ OR=PR+QR
因此證明了 OR=PR+QR
更新於： 2022年10月10日
100 次瀏覽
廣告