資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
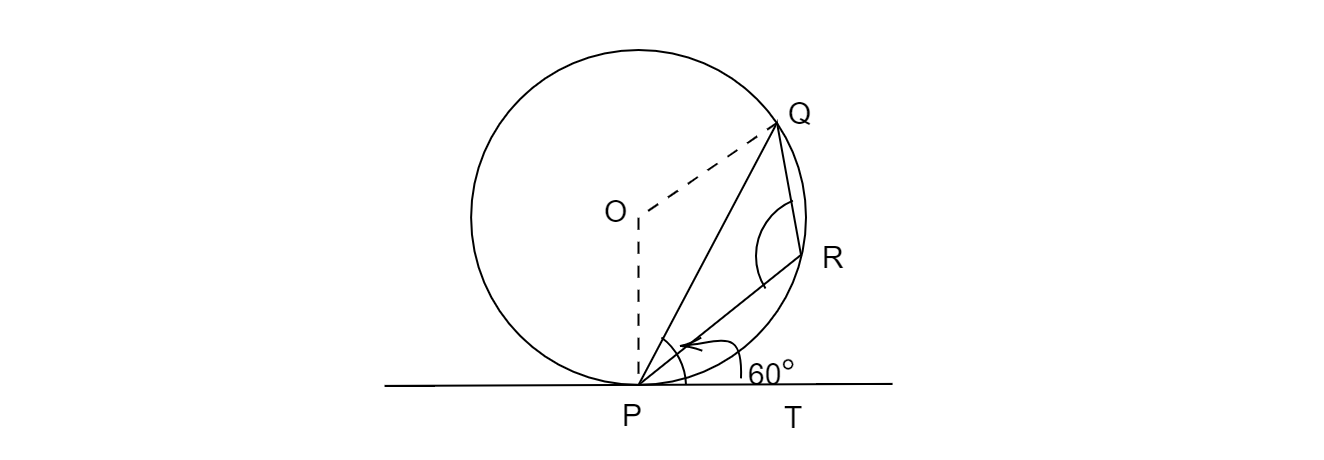
法律研究在下圖中，PQ 是圓 O 的弦，PT 是切線。如果∠QPT = 60°，求∠PRQ。
"\n
已知：圓 O 的弦 PQ 和切線 PT。其中 P 為切點。∠QPT=60°
求解：求∠PRQ=?
解
∠OPT=90° （∵半徑始終垂直於切點處的切線）
所以，∠OPQ=∠OPT-∠QPT
=90°-60°
=30°
現在在△OPQ 中，
∠OPQ=∠OQP=30° （∵OP=OQ=圓的半徑）
∴ ∠POQ=180°-（30° + 30°）
=120°
眾所周知，△OPQ 有一個反射△PEQ。
∴ ∠POQ=∠PRQ=120°
因此∠PRQ=120°。
更新於： 2022年10月10日
64 次瀏覽
廣告