資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
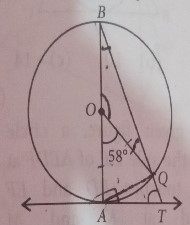
法學在給定的圖形中，\(AB\)是圓的直徑，圓心為\(O\)，\(AT\)是切線。如果\(∠AOQ=58°\)，求\(∠ATQ\)。
已知
AB是給定圓的直徑，AT是切線。
∠AOQ=58°。
要求
我們必須求出∠ATQ。
解答
AB是直徑。這意味著它是一條直線。
∠AOQ + ∠BOQ = 180°
∠BOQ = 180° - 58°
∠BOQ = 122°
在三角形BOQ中，
OB = OQ (圓的半徑)
∠OBQ = ∠OQB (等邊對等角)
∠OBQ + ∠OQB + ∠BOQ = 180°
122° + 2(∠OBQ) = 180°
2∠OBQ = 180° - 122°
∠OBQ = 58°/2
∠OBQ = 29°
在三角形ABT中，
∠ABT + ∠BAT + ∠BTA = 180°
29° + 90° + ∠BTA = 180° (∠ABT = ∠OBQ，且∠BAT = 90°，因為AT是圓的切線)
∠ATQ = 180° - 119° (∠BTA = ∠ATQ)
∠ATQ = 61°
∠ATQ的度數是61°。
更新於：2022年10月10日
73 次瀏覽
廣告