如圖所示，$O$是圓的圓心。如果$\angle BAC=130^{\circ}$，則求$\angle BOC$。"\n

已知：在給定圖形中，$O$是圓的圓心，$\angle BAC=130^{\circ}$。

求解：求$\angle BOC$。

解

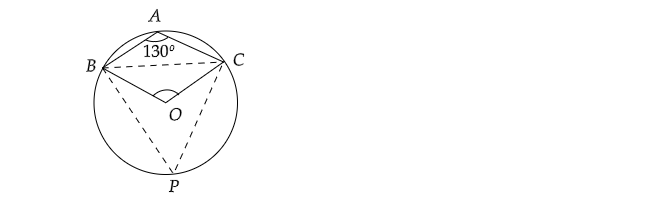
連線$BC$。現在，在圓周上取一點$P$，並連線$PB$和$PC$。

$PBAC$是一個圓內接四邊形。

已知四邊形中對角和為$180^{\circ}$。

$\therefore \angle BAC+\angle BPC=180^{\circ}$

$\Rightarrow 130^{\circ}+\angle BPC=180^{\circ}-130^{\circ}=50^{\circ}$

我們知道，$BC$是圓的弦。

圓的弦在圓心處所對的角是它在圓周上所對的角的兩倍。

因此，$\angle BOC=2\angle BPC$

$\Rightarrow \angle BOC=50^{\circ}\times2=100^{\circ}$

因此，$\angle BOC=100^{\circ}$。

教程點

更新於： 2022年10月10日

170 次瀏覽

開啟你的 職業生涯

完成課程獲得認證

開始學習