如圖所示，從圓外一點 \( P \) 引圓的切線 \( P Q \) 和 \( P R \)，使得 \( \angle R P Q=30^{\circ} \)。作弦 \( R S \) 平行於切線 \( P Q \)。求 \( \angle R Q S \)。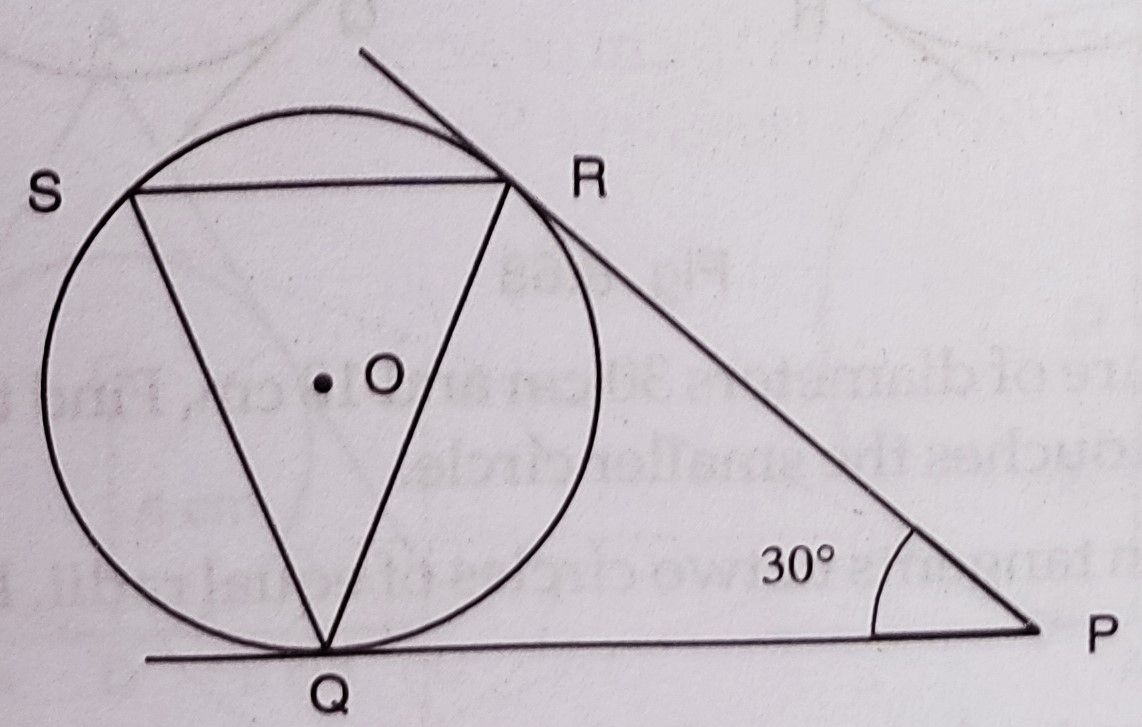"\n

已知

如圖所示，從圓外一點 \( P \) 引圓的切線 \( P Q \) 和 \( P R \)，使得 \( \angle R P Q=30^{\circ} \)。作弦 \( R S \) 平行於切線 \( P Q \)。

要求

我們要求 \( \angle R Q S \)。

解答

$PQ$ 和 $PR$ 是從點 $P$ 引出的圓心為 $O$ 的圓的切線，且 $\angle RPQ = 30^o$

$RS\ \parallel\ PQ$.
$PQ = PR$    (從圓外一點引出的圓的切線相等)

$\angle PRQ = \angle PQR$

$\angle PRQ=\angle PQR=\frac{180^{\circ}-30^{\circ}}{2}$

$=\frac{150^{\circ}}{2}=75^{\circ}$

$\angle SRQ=\angle PQR=75^{\circ}$

$\angle RSQ=\angle QRS$      (因為 $QR=QS$)

$=75^{\circ}$

在 $\Delta QRS$ 中，

$\angle RQS=180^{\circ}-(\angle RSQ+\angle QRS)$

$=180^{\circ}-(75^{\circ}+75^{\circ})$

$=180^{\circ}-150^{\circ}$

$=30^{\circ}$

因此，$\angle RQS=30^{\circ}$.

教程點

更新於: 2022年10月10日

85 次瀏覽

開啟你的職業生涯

完成課程，獲得認證

立即開始