如圖所示，\( O Q: P Q=3: 4 \)，且\( \Delta P O Q \)的周長為\( 60 \mathrm{~cm} \)。求\( P Q, Q R \)和\( O P \)的值。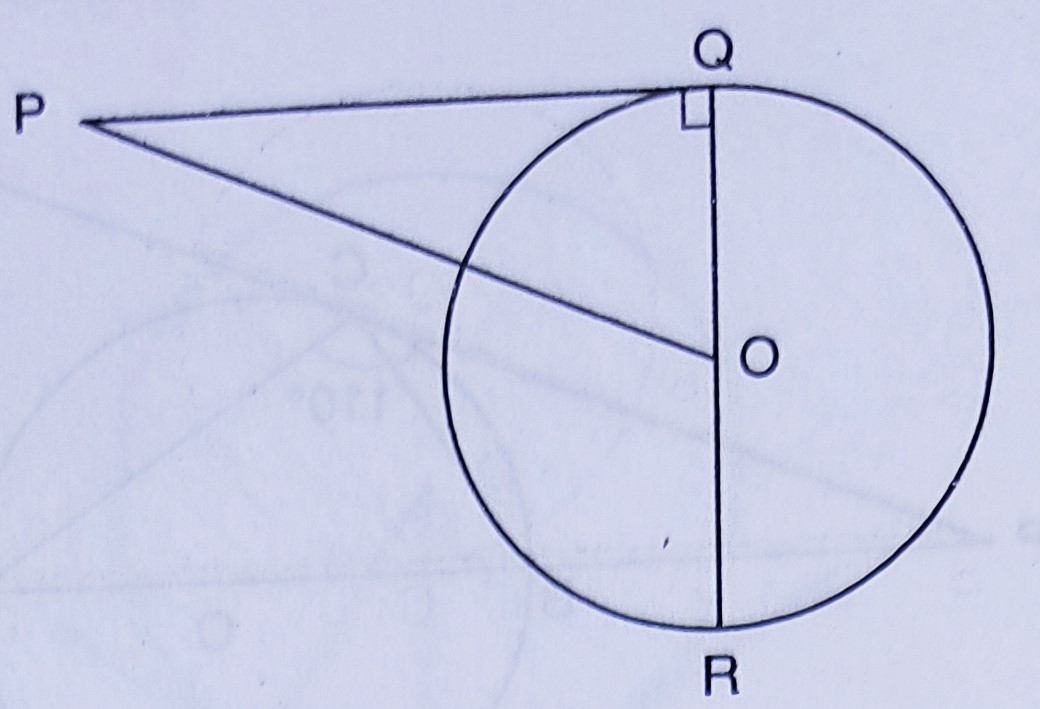

已知

如圖所示，\( O Q: P Q=3: 4 \)，且\( \Delta P O Q \)的周長為\( 60 \mathrm{~cm} \).

解題步驟：
我們需要求出\( P Q, Q R \)和\( O P \)的值。

 解答

如圖所示：

$OQ : PQ = 3:4$

$\triangle POQ$的周長 = 60 cm

設 $OQ = 3x$，$PQ = 4x$

在直角三角形 $OPQ$ 中：

$OP^2 = OQ^2 + PQ^2$

$= (3x)^2 + (4x)^2$

$= 9x^2 + 16x^2$

$= 25x^2$

$= (5x)^2$

$\Rightarrow OP = 5x$

$OQ + QP + OP = 60\ cm$

$3x + 4x + 5x = 60$

$12x = 60$

$x = 5$

$PQ = 4x = 4 \times 5 = 20\ cm$

$QR = 2 OQ = 2(3x) = 6 \times 5 = 30\ cm$

$OP = 5x = 5 \times 5 = 25\ cm$

因此，\(PQ=20\ cm\)，\(QR= 30\ cm\)，\(OP=25\ cm\).

教程點

更新於：2022年10月10日

76 次瀏覽

開啟你的職業生涯

完成課程並獲得認證

開始學習