如圖所示，有兩個同心圓，圓心為 O。\( P R T \) 和 \( P Q S \) 是從外圓上一點 \( P \) 引到內圓的切線。如果 \( P R=5 \mathrm{~cm} \)，求 \( P S \) 的長度。"\n

已知

如圖所示，有兩個同心圓，圓心為 O。\( P R T \) 和 \( P Q S \) 是從外圓上一點 \( P \) 引到內圓的切線。

\( P R=5 \mathrm{~cm} \).

要求：
我們需要求出 \( P S \) 的長度。

 解答

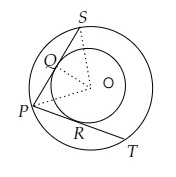
連線 $OS$ 和 $OP$。

在 $\triangle POS$ 中，

$PO = OS$

這意味著，

$\triangle POS$ 是一個等腰三角形。

我們知道，

在一個等腰三角形中，如果從等腰三角形兩腰的公共頂點向底邊作垂線，那麼這條垂線將平分底邊。

$PQ = PR = 5\ cm$   ($PRT$ 和 $PQS$ 是從外圓上一點 $P$ 引到內圓的切線)

$PQ = QS$

$PQ = 5\ cm$

$QS = 5\ cm$

從圖中可以看出，

$PS = PQ + QS$

$PS = 5 + 5$

$PS = 10\ cm$

\( P S \) 的長度為 $10\ cm$。

Tutorialspoint

更新於： 2022年10月10日

80 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習