資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究從外部一點\( P \)，作圓的切線\( P A \)和\( P B \)，圓心為\( O \)。在圓上一點\( E \)處作切線，該切線分別與\( P A \)和\( P B \)相交於\( C \)和\( D \)。如果\( P A=14 \mathrm{~cm} \)，求\( \triangle P C D \)的周長。
已知
從外部一點\( P \)，作圓的切線\( P A \)和\( P B \)，圓心為\( O \)。在圓上一點\( E \)處作切線，該切線分別與\( P A \)和\( P B \)相交於\( C \)和\( D \)。
\( P A=14 \mathrm{~cm} \)。
要求
我們要求出\( \triangle P C D \)的周長。
解答
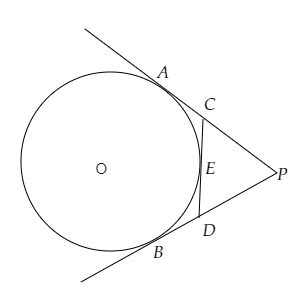
$PA$ 和 $PB$ 是從圓外一點 $P$ 引出的圓的切線，圓心為 $O$。
$CD$ 是圓在點 $E$ 處的另一條切線，它分別與 $PA$ 和 $PB$ 相交於 $C$ 和 $D$。
$PA = 14\ cm$
$PA$ 和 $PB$ 是從 $P$ 引出的圓的切線
$PA = PB = 14\ cm$
$CA$ 和 $CE$ 是從 $C$ 引出的切線
這意味著，
$CA = CE$...….(i)
類似地，
$DB$ 和 $DE$ 是從 $D$ 引出的切線
$DB = DE$....….(ii)
$\triangle PCD$ 的周長 $= PC + PD + CD$
$= PC + PD + CE + DE$
$= PC + CE + PD + DE$
$= PC + CA + PD + DB$ [根據 (i) 和 (ii)]
$= PA + PB$
$= 14 + 14$
$= 28\ cm$
$\triangle PCD$ 的周長是 $28\ cm$。
更新於: 2022年10月10日
114 次瀏覽
廣告