從點\( P \)引出兩條切線\( PA \)和\( PB \)與圓心為\( O \)的圓相切。如果\( OP \)等於圓的直徑，證明\( \triangle APB \)是等邊三角形。

已知

從點\( P \)引出兩條切線\( PA \)和\( PB \)與圓心為\( O \)的圓相切。

\( OP \)等於圓的直徑。

要求

我們必須證明\( \triangle APB \)是等邊三角形。

解答

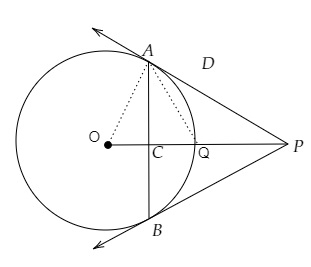
連線 $AB, OP, AQ, OA$。

設圓的半徑為 $r$。

這意味著：

$OP = 2r$

$OQ + QP = 2r$

$OQ = QP = r$

在直角三角形 $OAP$ 中，

$OP$ 是斜邊，$Q$ 是其中點。

$OA = AQ = OQ$ (直角三角形斜邊中點到頂點的距離相等)

因此，

$\triangle OAQ$ 是等邊三角形，$\angle AOQ = 60^o$。

在直角三角形 $OAP$ 中，

$\angle APO = 90^o - 60^o = 30^o$

$\angle APB = 2 \angle APO = 2 \times 30^o = 60^o$

$PA = PB$ (從同一點引出的圓的切線長度相等)

$\angle PAB = \angle PBA = 60^o$

這意味著：

$\triangle APB$ 是等邊三角形。

證畢。

教程點

更新於：2022年10月10日

瀏覽量：138

啟動你的職業生涯

完成課程獲得認證

開始學習