設 \( A \) 為圓外一點，該圓的圓心為 \( O \)，半徑為 \( 5 \mathrm{~cm} \)，\( A \) 與 \( O \) 的距離為 \( 13 \mathrm{~cm} \)。\( AP \) 和 \( AQ \) 為圓在 \( P \) 和 \( Q \) 點的切線。若在小弧 \( PQ \) 上一點 \( R \) 作切線 \( BC \)，與 \( AP \) 交於 \( B \) 點，與 \( AQ \) 交於 \( C \) 點，求三角形 \( ABC \) 的周長。

---

已知

\( A \) 為圓外一點，該圓的圓心為 \( O \)，半徑為 \( 5 \mathrm{~cm} \)，\( A \) 與 \( O \) 的距離為 \( 13 \mathrm{~cm} \)。\( AP \) 和 \( AQ \) 為圓在 \( P \) 和 \( Q \) 點的切線。

在小弧 \( PQ \) 上一點 \( R \) 作切線 \( BC \)，與 \( AP \) 交於 \( B \) 點，與 \( AQ \) 交於 \( C \) 點。

要求

求三角形 \( ABC \) 的周長。

解題過程

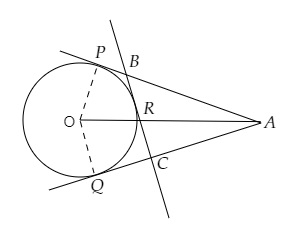
$\angle OPA = 90^o$    (圓上一點的切線垂直於過該點的半徑)

在直角三角形 \( OPA \) 中，

$OA^2 = OP^2 + PA^2$    (勾股定理)

$(13)^2 = 5^2 + PA^2$

$PA^2 = 169-25$

$=144$

$=(12)^2$

$\Rightarrow PA = 12\ cm$

三角形 \( ABC \) 的周長 \( = AB + BC + CA \)

$= (AB + BR) + (RC + CA)$

$= AB + BP + CQ + CA$   (因為 \( BR = BP \) 和 \( RC = CQ \)，從圓內一點到圓的兩條切線長度相等)

$= AP + AQ$ 

$= 2AP$        (從圓內一點到圓的兩條切線長度相等)

$= 2 \times 12$

$= 24\ cm$

三角形 \( ABC \) 的周長為 \( 24\ cm \)。