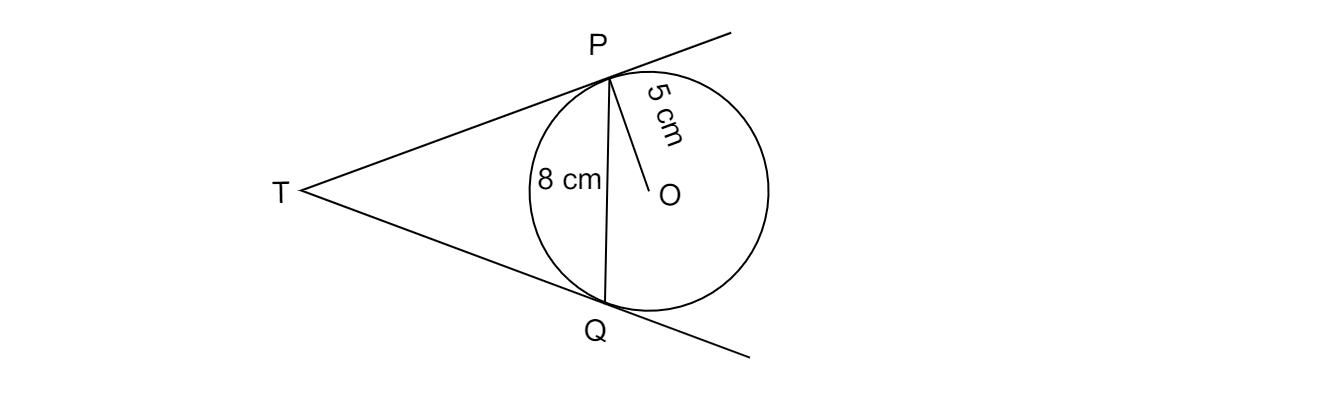
如圖所示，$PQ$是半徑為$5\ cm$、圓心為$O$的圓的一條弦，長度為$8\ cm$。$P$和$Q$處的切線相交於點$T$。求$TP$的長度。

"\n

已知：弦長$PQ=8\ cm$，圓的半徑$OP=5\ cm$。

求解：求$TP$的長度。

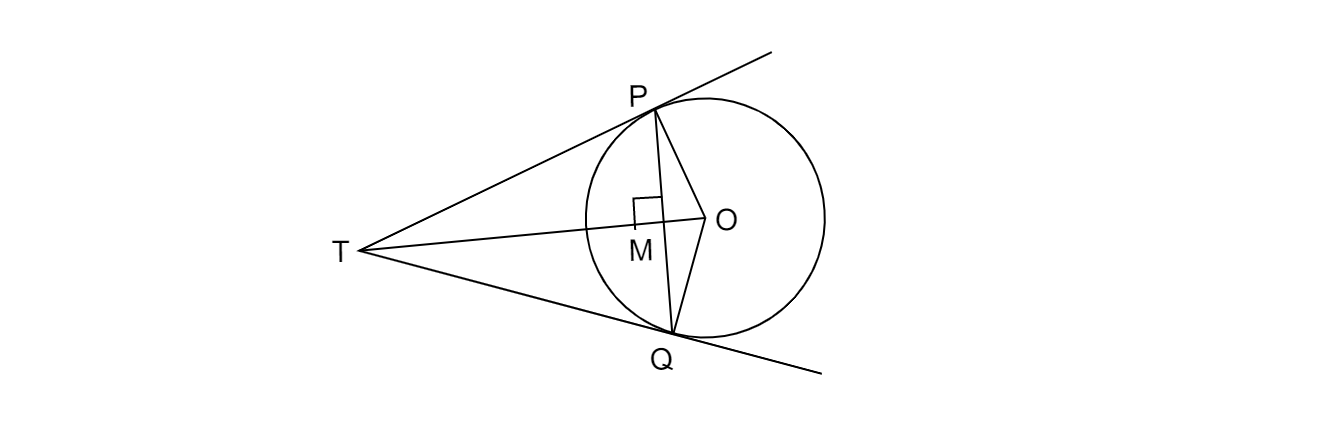
已知半徑$OP=OQ=5\ cm$

弦長

$PQ=8\ cm $

$OT \perp PQ$。

$\because$ 從圓心到弦的垂線平分弦。

$\therefore PM=MQ=4\ cm$  

在直角$\vartriangle OPM$中，

$(OP)^{2}=(PM)^{2} +(OM)^{2}$ 

$\Rightarrow(5)^{2}=(4)^{2}+(OM)^{2}$

$\Rightarrow ( OM)^{2}=25-16=9$

$\Rightarrow OM=\sqrt{9}$

$\Rightarrow OM=3\ cm$

$\angle OPT=90^{o} $                        [半徑垂直於切線在切點處]

在直角$\vartriangle OPT$中，

$( OT)^{2}=( PT)^{2}+( OP)^{2}$                              ....................$( 1)$

在直角$\vartriangle PTM$中，

$( PT)^{2}=( TM)^{2} +( PM)^{2}$                       ......................... $( 1)$

由公式$( 1)$和$( 2)$，

$( OT)^{2}=( PT)^{2}+( OP)^{2}=( TM)^{2} +( PM)^{2} +( OP)^{2}$   

$\Rightarrow ( TM+OM)^{2}=( TM)^{2} +( PM)^{2} +( OP)^{2}$   

$\Rightarrow ( TM)^{2}+( OM)^{2}+2\times TM\times OM=( TM)^{2} +( PM)^{2} +( OP)^{2} $

$\Rightarrow (OM)^{2}+2\times TM\times OM=(PM)^{2} +(OP)^{2} $

$\Rightarrow  (3)^{2}+2\times 3\times TM=(4)^{2}+(5)^{2}$

$\Rightarrow 9+6TM=16+25=41$

$\Rightarrow 6TM=41-9=32$

$\Rightarrow TM=\frac{32}{6}=\frac{16}{3}\ cm$

將$TM=\frac{16}{3}\ cm$代入公式$( 2)$，

$( PT)^{2}=( TM)^{2} +( PM)^{2}$

$\Rightarrow ( PT)^{2}=(\frac{16}{3})^{2} +(4)^{2}$

$\Rightarrow ( PT)^{2}=\frac{256}{9}+16$

$\Rightarrow ( PT)^{2}=\frac{256+144}{9}$

$\Rightarrow ( PT)^{2}=\frac{400}{9}$

$\Rightarrow PT=\sqrt{\frac{400}{9}}$

$\Rightarrow PT=\frac{20}{3} cm$

因此$PT=\frac{20}{3}\ cm$。