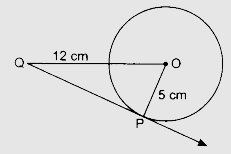
半徑為 5 釐米的圓上一點 P 的切線 PQ 與過圓心 O 的一條直線交於點 Q，使得 OQ = 12 釐米。求 PQ 的長度。
(a) 12 釐米
(b) 13 釐米
(c) 8.5 釐米
(d) $\sqrt{199}$ 釐米

已知

半徑為 5 釐米的圓上一點 P 的切線 PQ 與過圓心 O 的一條直線交於點 Q，使得 OQ = 12 釐米。

要求

我們需要求 PQ 的長度。

解答：  

圓的半徑 = 5 釐米

OQ = 12 釐米

我們知道：

圓的切線垂直於過切點的半徑。

∠OPQ = 90°

因此，根據勾股定理，

PQ² + OP² = OQ²

PQ² = OQ² - OP²

PQ² = 12² - 5²

$= 144 - 25$

$= 119$

PQ = $\sqrt{119}$ 釐米

因此，PQ 的長度為 $\sqrt{119}$ 釐米。

教程點

更新於：2022年10月10日

78 次瀏覽

開啟您的 職業生涯

完成課程獲得認證

開始學習