O 是半徑為 8 釐米的圓的圓心。圓上一點 A 的切線與過 O 的直線相交於 B 點，使得 AB = 15 釐米。求 OB 的長度。

已知

O 是半徑為 8 釐米的圓的圓心。圓上一點 A 的切線與過 O 的直線相交於 B 點，使得 AB = 15 釐米。

求解

我們需要求出 OB 的長度。

解答

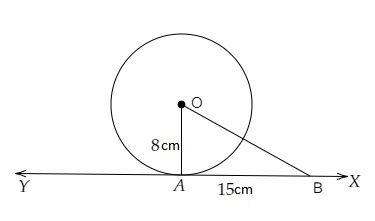
半徑 OA = 8 釐米。

AB = 15 釐米

設 XY 為圓在 A 點的切線。

OA ⊥ XY

在直角三角形 OAB 中，

根據勾股定理，

OB² = OA² + AB²

OB² = 8² + 15²

$= 64 + 225$

$= 289$

$= 17^2$

因此，

OB = 17 釐米

OB 的長度為 17 釐米。

教程點

更新於：2022年10月10日

80 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習