如果 PT 是一個圓的切線，該圓的圓心為 O，且 $OP = 17\ cm$，$OT = 8\ cm$。求切線段 PT 的長度。

---

已知

PT 是一個圓的切線，該圓的圓心為 O，且 $OP = 17\ cm$，$OT = 8\ cm$。

要求

我們必須找到切線段 PT 的長度。

解答

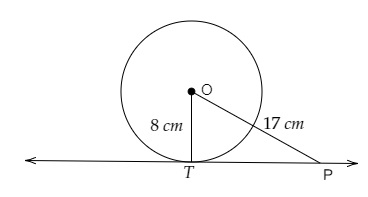
$OP = 17\ cm$ 且 $OT = 8\ cm$

$PT$ 是圓在 $T$ 點的切線。

$OT\ perp\ PT$

在直角三角形 $OTP$ 中，

根據勾股定理，

$OP^2= OT^2+ TP^2$

$17^2 = 8^2 + TP^2$

$TP^2= 289 - 64$

$= 225$

$= 15^2$

因此，

$TP = 15\ cm$

切線段 PT 的長度為 15 cm。