資料結構
網路
關係型資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法學研究已知三角形\( P Q R \)外接一個半徑為\( 8 \mathrm{~cm} \)的圓，\( Q R \)被切點\( T \)分成\( Q T = 14 \mathrm{~cm} \)和\( T R = 16 \mathrm{~cm} \)兩段。如果\( \Delta P Q R \)的面積為\( 336 \mathrm{~cm}^{2} \)，求邊長\( P Q \)和\( P R \)。
已知
三角形\( P Q R \)外接一個半徑為\( 8 \mathrm{~cm} \)的圓，\( Q R \)被切點\( T \)分成\( Q T = 14 \mathrm{~cm} \)和\( T R = 16 \mathrm{~cm} \)兩段。
\( \Delta P Q R \)的面積為\( 336 \mathrm{~cm}^{2} \)。
要求：
求邊長\( P Q \)和\( P R \)。
解答
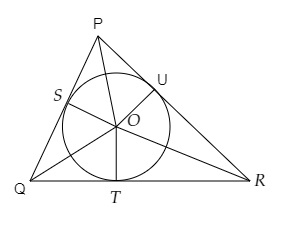
$\triangle PQR$ 外接圓心為 $O$，半徑為 $8\ cm$。
$T$ 是切點，它將線段 $QR$ 分成兩部分：
$QT = 14\ cm$ 和 $TR = 16\ cm$。
$\triangle PQR$ 的面積 $= 336\ cm^2$
設 $PS = x\ cm$
$QT$ 和 $QS$ 是從 $Q$ 引出的圓的切線。
$QS = QT = 14\ cm$
類似地，
$RU$ 和 $RT$ 是圓的切線
$RT = RU = 16\ cm$
$PS$ 和 $PU$ 是從 $P$ 引出的切線
$PS = PU = x\ cm$
$PQ = x + 14$，$PR = x + 16$，$QR = 14 + 16 = 30\ cm$
$\triangle PQR$ 的面積 = $\triangle POQ$ 的面積 + $\triangle QOR$ 的面積 + $\triangle POR$ 的面積
$\Rightarrow 336=\frac{1}{2}(\mathrm{QR}) \times 8+\frac{1}{2}(14+x) \times 8+\frac{1}{2}(16+x) \times 8$
$\Rightarrow 336=\frac{1}{2} \times 30 \times 8+4(14+x)+4(16+x)$
$\Rightarrow 336=120+56+4 x+64+4 x$
$\Rightarrow 336=8 x+240$
$\Rightarrow 8 x=336-240$
$\Rightarrow 8x=96$
$\Rightarrow x=\frac{96}{8}=12$
因此，$\mathrm{PQ}=x+14=12+14=26 \mathrm{~cm}$
$\mathrm{PR}=x+16=12+16=28 \mathrm{~cm}$
邊長\( P Q \)和\( P R \)分別為 $26\ cm$ 和 $28\ cm$。
瀏覽量：110
