資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝學
法學已知圓心為O的圓外一點P，引圓的兩條切線PQ和PR，且∠QPR=120°，求證：2PQ=PO。
已知：圓心為O的圓外一點P，引圓的兩條切線PQ和PR，且∠QPR = 120°
求證：2PQ=PO。
證明：
作圓，外接點P及兩條切線PQ和PR。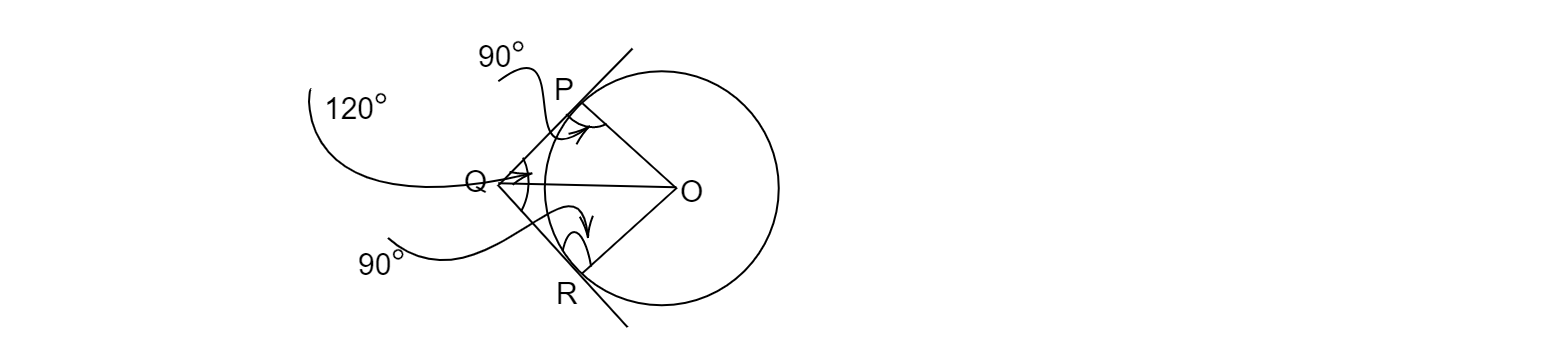
我們知道，半徑垂直於切線在切點的切線。
∠OQP=90°
我們也知道，從圓外一點引出的兩條切線與連線該點和圓心的線段等角。
∠QPO=60°
在△QPO中
cos60°=PQ/PO
⇒ 1/2 = PQ/PO
⇒ PO=2PQ
因此證明了PO=2PQ。
更新於：2022年10月10日
瀏覽量：139
廣告