資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會研究
服裝研究
法律研究如果從外一點 P 引出到半徑為 a、圓心為 O 的圓的兩條切線的夾角為 60°，則求 OP 的長度。
已知：圓的半徑 = a，從外點 P 引出的兩條切線的夾角 = 60°
求解：求 OP 的長度。
解
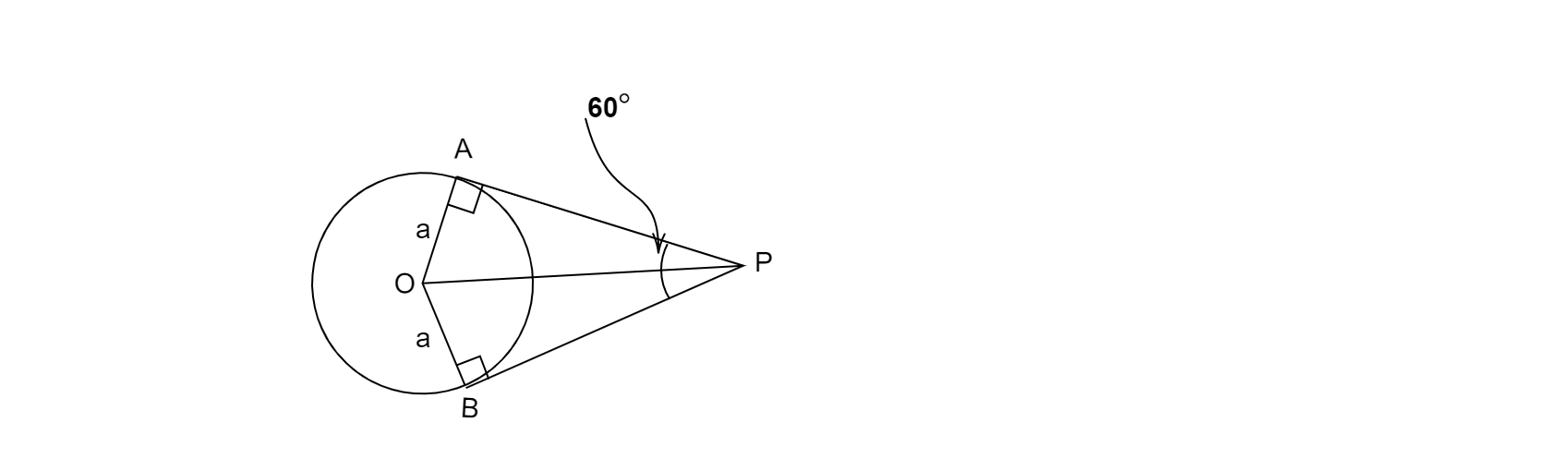
已知∠BPA = 60°
OB = OA = a (圓的半徑)
PA = PB (切線長度相等，OP = OP)
△PBO 和 △PAO 全等。(SSS 全等)
∠BPO = ∠OPA = 60°/2 = 30°
在△PBO 中，
sin 30° = a/OP
⇒ 1/2 = a/OP
⇒ OP = 2a 個單位
更新於：2022年10月10日
71 次瀏覽
廣告